Россия
Севастополь, Россия
сотрудник
В рамках линейного приближения теории длинных волн на основе гидродинамической численной модели ADCIRC исследуются резонансные свойства акваторий севастопольских бухт: Стрелецкой, Круглой, Камышовой, Двойной, включающей в себя б. Казачью и Соленую. Расчеты проведены для акватории каждой бухты отдельно на основе численных экспериментов. На первом этапе моделирования возбуждаются волны в акваториях бухт с помощью задания на жидкой границе, находящейся у входа в бухту, возмущения типа «красный шум». На втором этапе рассчитываются свободные колебания с условием свободного прохождения на жидкой границе. С использованием спектрального анализа установлены резонансные периоды указанных бухт и пространственное распределение спектральной плотности колебаний уровня в их акваториях для отдельных собственных мод. Большинство выделенных резонансных периодов для севастопольских бухт удовлетворительно согласуются с аналитическими оценками. Использование при моделировании данных батиметрии и профиля береговой черты, приближенных к реальным, позволило получить для всех рассмотренных бухт дополнительные резонансные периоды, которые нельзя получить при аналитических оценках. В б. Двойной, включающей в себя б. Казачью и Соленую, выявлено расширение спектрального состава резонансных мод, возникающее из-за связи этих бухт через их входы. Анализ пространственного распределения спектральной плотности основных энергонесущих колебаний уровня в б. Стрелецкой, Круглой, Камышовой, Двойной показал, что максимальные значения спек- тральной плотности возникают в основном в вершинах бухт. В б. Двойной максимальные значения спектральной плотности проявляются в восточном или западном рукавах (б. Казачья или Соленая соответственно) в зависимости от того, к какому из рукавов относится собственный период. Полученные здесь результаты могут быть использованы при проектировании размещения гидротехнических сооружений, развитии марикультуры, планировании выпусков сточных вод и т. п.
сейшевые колебания, сейши, севастопольские бухты, модель ADCIRC, математическое моделирование
Введение
Береговая линия г. Севастополя, расположенного в основном в пределах Гераклейского п-ова, изрезана множеством бухт и мысов, которые образуют систему, состоящую из главной бухты – Севастопольской – и связанных с ней бухт меньших размеров. В подобных водоемах часто наблюдаются сейши – стоячие колебания массы воды. Они отличаются от сейш в полностью замкну- тых бассейнах тем, что возбуждаются вследствие проникновения длинных волн из открытого моря через жидкую границу, при этом потери волновой энергии в основном происходят в результате ее излучения через вход в бухту [1]. В бухтах, в отличие от замкнутых водоемов, также генерируется мода Гельмгольца (нулевая мода), которая обычно доминирует над всеми осталь- ными видами собственных колебаний и определяет общий характер движе- ний в акватории [2, 3]. Опасность сейш в бухтах состоит в том, что они могут быть причиной интенсивных периодических течений, представляющих угрозу для береговой инфраструктуры и судов [4]. Известно также, что примыкаю- щие друг к другу бухты могут взаимодействовать друг с другом путем обмена энергией через свои открытые границы, что проявляется в проникновении собственных мод одной бухты в другую [5, 6]. Севастопольские бухты обра- зуют систему связанных осцилляторов, в результате чего в каждой из бухт модовый состав сейш расширяется.
Периоды сейшевых колебаний определяются геометрическими парамет- рами акватории: глубиной, очертаниями береговой линии, рельефом дна. Известно, что в черноморских бухтах и заливах периоды сейш имеют про- должительность от нескольких минут до двух часов, при этом периоды в ин- тервале 5–10 мин встречаются во всех бухтах и заливах. Колебания уровня с периодами 2–3 мин могут быть вызваны трансформацией длинных волн в прибрежной зоне или резкими порывами ветра одного направления. Колеба- ния с периодами 15–20 мин могут возникать при резких колебаниях атмосфер- ного давления, а также изменениях направления и скорости ветра. Наиболее часто сейши этого типа появляются при прохождении циклонов, особенно в зоне периферии, обусловливающей усиление ветра [7]. При этом наиболь- шую повторяемость имеют колебания уровня с периодом до 10 мин. Из сейш большего периода Крымского побережья наиболее часты сейши с периодом 30–50 мин [7]. В результате анализа данных кратковременных измерений, выполненных с помощью ADCP-зонда во время экспедиций Морского гид- рофизического института в 2008 и 2014 гг., было установлено, что у входа в б. Севастопольскую флуктуации течений происходят с периодом около 60 мин [8].
Помимо сейш, в севастопольских бухтах фоном проявляются приливные колебания уровня, присущие Черному морю. В работе [9], посвященной ис- следованию черноморских приливов, указывается, что на побережье Крыма наиболее интенсивны главная лунная полусуточная составляющая 12.42 ч и гравитационная лунно-солнечная суточная составляющая 23.93 ч. Значения интенсивности этих приливных мод близки друг к другу, что хорошо согла- суется с данными из работы [10].
В настоящее время сейшевые колебания в севастопольских бухтах оста- ются малоисследованными. Данные натурных наблюдений имеются только для б. Севастопольской и Круглой. Колебания уровня моря в б. Севастополь- ской фиксировались с помощью мареографа, расположенного на морской гидрометеорологической станции на Павловском мысу [10]. В процессе об- работки результатов натурных наблюдений выделены периоды, соответству- ющие полусуточной и суточной составляющим прилива, а также со значени- ями 0.9, 1.25, 2.5 ч. Колебание с периодом 0.9 ч является модой Гельмгольца б. Севастопольской. В б. Круглой данные были получены относительно недав- но (в 2023 г.), при этом с помощью ультразвукового датчика были проведены измерения уровня и на основе спектрального анализа выявлены резонансные периоды локальных сейш [11]. Среди них выделена наиболее интенсивная мо- да Гельмгольца б. Круглой с периодом 13.7 мин.
Установление физических закономерностей колебаний уровня в системе связанных бухт, таких как севастопольские, представляется возможным при помощи математического моделирования. Ряд работ [1, 6, 11, 12] посвящен исследованиям сейшевых колебаний в некоторых бухтах Севастополя на ос- нове численного моделирования. В [6] исследовалось взаимное влияние б. Севастопольской и Карантинной друг на друга вследствие обмена энергией колебаний через их входы. Показано, что интенсивность собственных мод б. Севастопольской, проникающих в б. Карантинную, может превосходить интенсивность собственных мод б. Карантинной. В работе [1] изучались ре- зонансные периоды основных севастопольских бухт и влияние длительности действия начального возмущения на генерацию в них сейш. В [12] исследо- ваны различные режимы сейшевых колебаний на примере б. Севастополь- ской для возмущений с периодами 2.5, 2.9 и 6.2 мин, относящимися к соб- ственным модам бухты с разной пространственной структурой. На основе численного решения задачи на собственные значения определены периоды фундаментальных мод б. Севастопольской (50 мин) [10] и Карантинной (9.25 мин) [13].
Тем не менее пока информации о периодах и пространственной структу- ре собственных колебаний уровня для всех севастопольских бухт недоста- точно. Поэтому возникает необходимость в построении целостной картины длинноволновых колебаний в севастопольских бухтах и определении значе- ний резонансных (собственных) периодов системы севастопольских бухт и ее отдельных элементов в высокочастотном диапазоне спектра (часы – минуты). Целью настоящей работы является изучение резонансного отклика уров-
ня моря в севастопольских бухтах: Стрелецкой, Круглой, Камышовой, Каза- чьей и Соленой – на возмущения, приходящие из открытого моря, и опреде- ление собственных периодов бухт. Резонансные свойства указанных бухт ис- следовали отдельно для каждой из них, что позволило наиболее детально исследовать модовый состав сейш. Знание резонансных свойств каждой из бухт системы позволит более точно интерпретировать результаты модели- рования и измерений для всей системы.
Материалы и методы исследований
Для подробного исследования сейшевых колебаний в севастопольских бухтах использовали батиметрические данные из оцифрованных морских карт. На рис. 1 представлен рельеф дна прибрежной зоны Севастополя с системой севастопольских бухт.
Численное моделирование проводилось отдельно для каждой из иссле- дуемых бухт: Стрелецкой, Круглой, Камышовой, Казачьей, Соленой. Рельеф дна этих бухт показан на рис. 2. Колебания уровня моря рассчитывали в точ- ках 1–23 (рис. 2).
Бухта Стрелецкая (рис. 2, а) расположена в трех километрах к юго- западу от южного мола б. Севастопольской, она врезается в берег на 2 км. Западнее б. Стрелецкой находится б. Круглая (рис. 2, b), по своей форме близкая к кругу. Бухта неглубокая c песчаным дном. Извилистая б. Камышовая (рис. 2, c) обособлена двумя защитными молами, ограничива- ющими ее вход. Длина ее составляет около 2.5 км. Бухты Казачья и Соленая (рис. 2, d) образуют так называемую б. Двойную, одну из наиболее сложных в системе севастопольских бухт. Она расположена в 15 км к западу от центра Севастополя, между б. Камышовой и м. Херсонес. Бухта Казачья длиннее Соленой приблизительно на 600 м.
Для расчетов применялась численная гидродинамическая модель ADCIRC (Advanced Circulation Model for Shelves Coasts and Estuaries) 1), 2). При этом использовался вариант модели [14], основанный на осредненных по глубине уравнениях движения
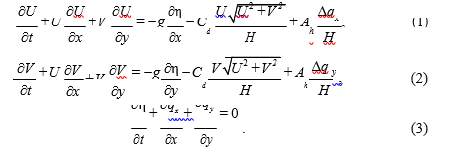
Здесь U, V – средние по глубине компоненты вектора скорости по осям x и y соответственно; h – уровень воды в бассейне; H = h + h – динамическая глу- бина; Cd – коэффициент донного трения; D – оператор Лапласа по простран- ственным переменным; Ah – коэффициент горизонтальной турбулентной вяз- кости; qx = UH, qy = VH – компоненты вектора полных потоков
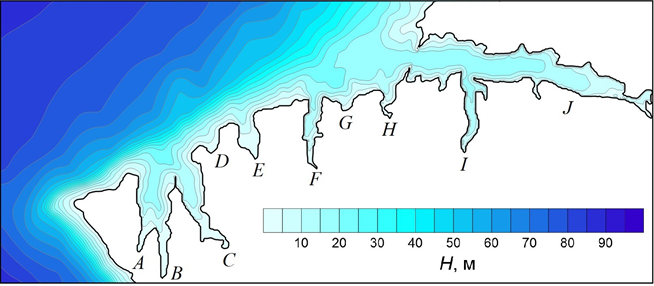
Р ис . 1 . Рельеф дна прибрежной зоны Севастополя. Обозначения бухт: A – Соленая, B – Казачья (эти две бухты образуют б. Двойную), C – Камышовая, D – Абрамова, E – Круглая, F – Стрелецкая, G – Песоч- ная, H – Карантинная, I – Южная, J – Севастопольская
F i g. 1. Bathymetry of the Sevastopol coastal zone. Notations: A – Solyo- naya Bay, B – Kazachya Bay (these two bays constitute Dvoynaya Bay), C – Kamyshovaya Bay, D – Abramova Bay, E – Kruglaya Bay, F – Streletskaya Bay, G – Pesochnaya Bay, H – Karantinnaya Bay, I – Yuzhnaya Bay, J – Se- vastopol Bay
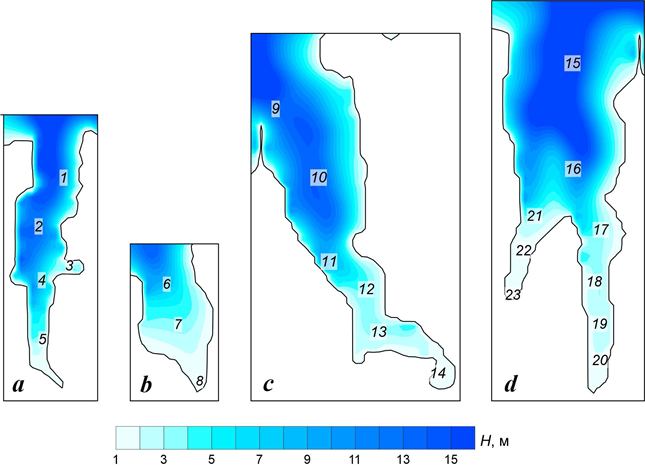
Р ис . 2 . Батиметрия севастопольских бухт: а – Стрелецкой; b – Круг- лой; c – Камышовой; d – Двойной. Цифрами 1–23 отмечены виртуаль- ные мареографы (станции)
F ig . 2 . Bathymetry of Sevastopol bays: а – Streletskaya; b – Kruglaya; c – Kamyshovaya; d – Dvoynaya. Numbers 1–23 stand for virtual mareo- graphs (stations)
Численный алгоритм модели ADCIRC базируется на методе конечных элементов, использующем треугольные элементы и линейные базисные функции. Для снижения уровня вычислительного шума при численном инте- грировании системы уравнение неразрывности представляется в виде так называемого уравнения GWCE (Generalized Wave Continuity Equation)
¶G
 ¶t + τ0G= 0,
¶t + τ0G= 0,
где
G º ¶η / ¶t + ¶qx / ¶x+ ¶qy / ¶y ; t0 – неотрицательный параметр, влияющий на фазовые характеристики и устойчивость численного алгоритма. После некоторых тождественных преобразований уравнение GWCE принимает вид
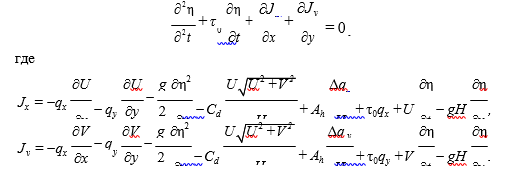
 Построенный на основе GWCE численный алгоритм решения системы уравнений эффективно подавляет коротковолновый шум без использования искусственной вязкости и без искажения характеристик длинноволнового участка спектра.
Построенный на основе GWCE численный алгоритм решения системы уравнений эффективно подавляет коротковолновый шум без использования искусственной вязкости и без искажения характеристик длинноволнового участка спектра.
Использовался квазилинейный вариант модели ADCIRC с учетом донно- го трения, поскольку предполагалось, что можно пренебречь вкладом нели- нейных слагаемых в уравнениях (1)–(3). Сила Кориолиса не учитывалась из-за ее слабого влияния в масштабах севастопольских бухт. Горизонтальная турбулентная вязкость также не учитывалась, поэтому коэффициент турбу- лентной вязкости Ah принимался равным нулю; параметр t0 составил 0.005.
Коэффициент донного трения ![]()
где C0 – минимальное значение Cd ; α = 10 – безразмерный параметр, определяющий скорость роста донного трения, когда глубина больше или меньше глубины обрушения волн Hb = 1 м; β = 1/3 – безразмерный параметр, определяющий, как увеличи- вается донное трение с уменьшением глубины бассейна.
Численное моделирование проводилось на неструктурированных расчет- ных сетках, которые насчитывали от ~ 4000 до ~ 12 200 конечных элементов для различных бухт. Пространственный шаг составил от 20 до 100 м. Шаг интегрирования по времени составил Δt = 0.025 c.
Генерация волн осуществлялась вследствие возмущения типа «красный шум» [15], задаваемого на жидкой границе каждой из рассматриваемых бухт. Граничное условие на жидкой границе имеет вид
ное значение Cd ; α = 10 – безразмерный параметр, определяющий скорость роста донного трения, когда глубина больше или меньше глубины обрушения волн Hb = 1 м; β = 1/3 – безразмерный параметр, определяющий, как увеличи- вается донное трение с уменьшением глубины бассейна.
Численное моделирование проводилось на неструктурированных расчет- ных сетках, которые насчитывали от ~ 4000 до ~ 12 200 конечных элементов для различных бухт. Пространственный шаг составил от 20 до 100 м. Шаг интегрирования по времени составил Δt = 0.025 c.
Генерация волн осуществлялась вследствие возмущения типа «красный шум» [15], задаваемого на жидкой границе каждой из рассматриваемых бухт. Граничное условие на жидкой границе имеет вид
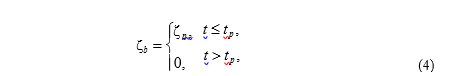
– случайная функция со спектром «красного шума»; t p – период времени накачки.
Численный эксперимент состоял из этапа накачки длительностью 6 ч и этапа свободных колебаний (6 ч). На этапе накачки на жидкой границе рас- четной области генерировались волновые возмущения вследствие задания условия (4). Использование помех в виде «красного шума» позволило пода- вить высокочастотные составляющие и учесть отклик системы бухт в длин- новолновом спектре. На этапе свободных колебаний применены начальные условия, сформированные на основе результатов проведенных на предыду- щем этапе расчетов. На жидкой границе расчетной области задавалось усло- вие свободного прохождения. По рассчитанным в режиме свободных колеба- ний рядам отклонений уровня с помощью спектрального анализа выделялись периоды мод с наибольшей интенсивностью.
Результаты моделирования и обсуждение
В результате численных экспериментов рассчитаны колебания уровня на ст. 1–23, которые расположены в расчетной области каждой из исследуе- мых бухт. На рис. 3 приведены мареограммы, рассчитанные для режима сво- бодных колебаний уровня.
Наиболее интенсивные сейшевые колебания возникают в б. Камышовой (рис. 3, c), Казачьей (рис. 3, d) и Соленой (рис. 3, e). Кроме того, сейши в данных бухтах затухают медленнее (в течение 2 ч), чем в б. Стрелецкой и Круглой (рис. 3, а, b), где затухание колебаний воды длится около 45 мин. Отметим, что б. Соленая и Казачья входят в состав б. Двойной (см. рис. 2, d), что накладывает свой отпечаток на характер колебаний в них: интенсивность сейш в более протяженной б. Казачьей выше, чем в б. Соленой. Это согласу- ется с результатами, полученными в работе [16], где исследовалась модельная разветвленная бухта, которая имеет характерные размеры, среднюю глубину и конфигурацию б. Двойной. В работе показано, что асимметрия приводит к уменьшению интенсивности колебаний в относительно короткой бухте и их значительным амплитудам в более длинной бухте, а также к расшире- нию модового состава сейшевых колебаний в обеих бухтах.
Для определения периодов сейшевых колебаний в бухтах рассчитанные мареограммы подвергались спектральному анализу (использовались скрипты, разработанные Gert Klopman и Delft Hydraulics 3)). C помощью преобразова- ния Фурье получены энергетические спектры колебаний уровня E (f). Спект- ральная плотность энергии ESD в диапазоне частот [fa; fb] рассчитывалась как
fb
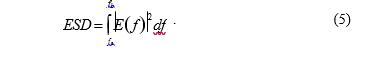
На рис. 4 приведены энергетиче- ские спектры колебаний уровня E (f) в вершинах бухт Севастополя. Видно, что в б. Стрелецкой доминируют мо- ды с периодами 1.1, 1.6, 2.8, 1.4 мин (рис. 4, а). В б. Круглой основные пики отмечаются на периодах 4.6, 10.6, 1.7,
2.7 мин (рис. 4, b). В б. Камышовой преобладают моды с периодами 7.1, 1.5, 3.6, 4.5, 2.1 мин (рис. 4, c). Казачья и Соленая, по сути, являются связан- ными бухтами, в результате чего мо- довый состав их сейш расширяется вследствие их взаимного влияния. Ос- новные пики в б. Казачьей приходятся на периоды 17.1, 2.7, 3.3, 1.6, 6.7 мин, в б. Соленой – на периоды 5.1, 17.1, 9.5, 6.7, 3.3, 2.0, 2.5 мин. Таким обра- зом, в обеих бухтах прослеживаются три одинаковых пика на периодах 17.1, 3.3, 6.7 мин.
В таблице представлены установ- ленные периоды мод резонансных колебаний для вершин бухт, периоды упорядочены по убыванию энергии колебаний. Здесь же указаны периоды собственных колебаний уровня моря в севастопольских бухтах, рассчитан- ные в работе [1] по формулам для бассейна постоянной глубины и для бассейна с параболическим профилем дна (эти значения указаны в скобках) из [17]. Из таблицы видно, что зна- чения большинства периодов, полу- ченные в настоящем исследовании, совпадают со значениями периодов,
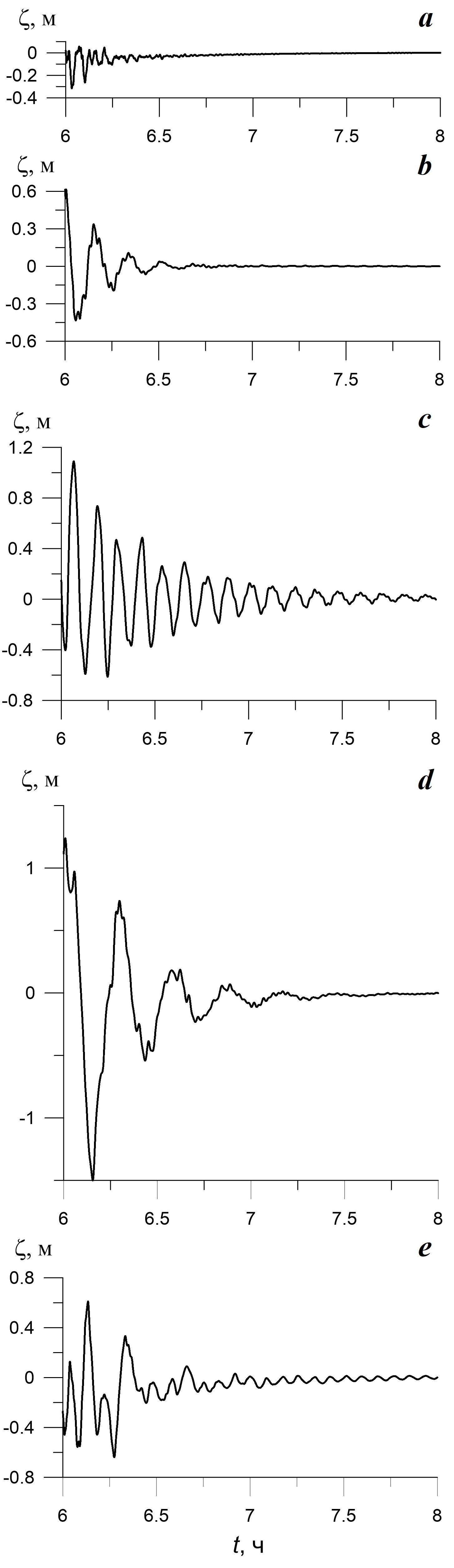
Р ис . 3 . Рассчитанные для режима сво- бодных колебаний мареограммы в бухтах Севастополя: а – Стрелецкой (ст. 5); b – Круглой (ст. 8); c – Камышовой (ст. 14); d – Казачьей (ст. 20); e – Соленой (ст. 23)
F i g. 3. Marigrams calculated for the free oscillations mode in Sevastopol bays: а – Stre- letskaya (St. 5); b – Kruglaya (St. 8); c – Ka- myshovaya (St. 14); d – Kazachya (St. 20); e – Solyonaya (St. 23)
найденных аналитически в работе [1],
или близки к ним. Отсутствие некото- рых значений и появление новых в по- лученных нами результатах связано со сложной формой бухт, отличной от прямоугольной, и особенностями рельефа дна. Так, в б. Стрелецкой вы- явлены все полученные ранее периоды, кроме периода 13.5 мин, соответству- ющего моде Гельмгольца данной бух- ты. Видимо, это связано с особенно- стями воздействия возмущения типа
«красный шум». В б. Круглой появля- ются новые моды с периодами 4.6, 1.9,
1.6 мин. Настоящие исследования вы- явили в б. Камышовой моду с перио- дом 12.9 мин, в то время как, по анали- тическим оценкам, максимальный пе- риод составил 19.8 мин. Что касается б. Казачьей и Соленой, которые обра- зуют б. Двойную, в этих бухтах выяв- лены почти все периоды, найденные аналитически. При этом модовый со- став колебаний уровня моря суще- ственно расширяется из-за связи бухт друг с другом через входы. Значения периодов, рассчитанные для б. Казачь- ей (6.7, 2.5, 2.0 мин) и Соленой (6.7, 3.3, 2.0, 2.5, 2.7 мин), также хорошо согла- суются и с полученными в работе [16] значениями для модельной бухты, ко- торая имеет конфигурацию и среднюю глубину б. Двойной. При этом насто- ящие исследования выявили для этих бухт более широкий диапазон периодов.
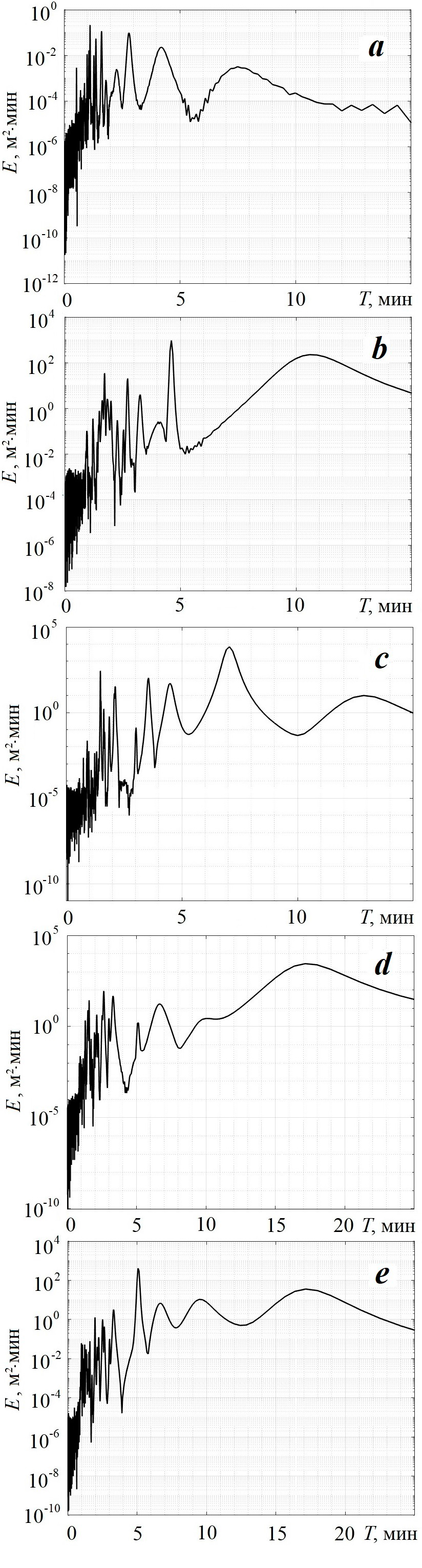
Р ис . 4 . Энергетические спектры коле- баний уровня, возникающих в результате воздействия возмущения в виде «красного шума» в бухтах Севастополя: а – Стрелец- кой (ст. 5); b – Круглой (ст. 8); c – Камы-
шовой (ст. 14); d – Казачьей (ст. 20); e –
Соленой (ст. 23)
F ig . 4 . Energy spectra of sea level oscil- lations resulting from red-noise disturbance in Sevastopol bays: а – Streletskaya (St. 5); b – Kruglaya (St. 8); c – Kamyshovaya (St. 14); d – Kazachya (St. 20); e – Solyonaya (St. 23)
Периоды собственных колебаний севастопольских бухт, мин., для бассейна постоян- ной глубины и для бассейна с параболическим профилем дна
Periods of natural oscillations in Sevastopol bays, min, for a stationary-depth basin and
a parabolic-bottom basin
|
Бухта (станция) / Bay (station) |
Периоды, выделенные на основе численного моделирования / Mathematically modelled periods |
Периоды, полученные на основе аналитической оценки [1] / Periods from analytical estimation [1] |
|
Б. Стрелецкая (ст. 5) / Streletskaya Bay (St. 5) |
1.3 1.6 2.8 1.4 4.2 |
13.5 4.5 (4.3) 2.7 (2.7) 1.9 (2.0) 1.3 1.2 |
|
Б. Круглая (ст. 8) / Kruglaya Bay (St. 8) |
4.6 |
10.2 3.4 (2.7) 2.0 (1.7) 1.5 (1.3) 3.0 2.3 |
|
2.7 10.6 1.7 3.3 1.9 1.6 2.0 |
||
|
1.5 |
||
|
Б. Камышовая |
7.1 |
19.8 |
|
1.5 |
6.7 (6.0) |
|
|
(ст. 14) / |
3.6 |
4.0 (3.8) |
|
Kamyshovaya Bay |
4.5 |
2.8 (2.8) |
|
(St. 14) |
2.1 |
1.5 |
|
12.9 |
1.4 |
|
|
Б. Казачья |
5.1 |
15.2 5.1 3.0 2.2 1.2 |
|
17.1 |
||
|
6.7 |
||
|
2.7 |
||
|
(восточный рукав б. Двойной) (ст. 20) / Kazachya Bay (eastern arm of Dvoynaya Bay) |
3.3 1.6 1.5 2.1 2.5 3.0 |
|
|
(St. 20) |
10.0 |
|
|
1.3 |
||
|
2.0 |
||
|
2.2 |
 Продолжение таблицы / Continued
Продолжение таблицы / Continued
|
Бухта (станция) / Bay (station) |
Периоды, выделенные на основе численного моделирования / Mathematically modelled periods |
Периоды, полученные на основе аналитической оценки [1] / Periods from analytical estimation [1] |
|
Б. Соленая (западный рукав б. Двойной) (ст. 23) / Solyonaya Bay (western arm of Dvoynaya Bay) (St. 23) |
5.1 17.1 2.0 9.5 6.7 3.3 2.5 2.7 2.2 3.0 1.6 |
9.6 3.2 1.9 1.4 1.3 1.2 |





 П р и м еч ан и е. Значения для бассейна с параболическим профилем дна указаны в скобках. Полужирным шрифтом выделены периоды, которые хорошо согласуются. Подчеркнуты периоды в б. Казачьей и Соленой, обусловленные взаимным влиянием бухт.
П р и м еч ан и е. Значения для бассейна с параболическим профилем дна указаны в скобках. Полужирным шрифтом выделены периоды, которые хорошо согласуются. Подчеркнуты периоды в б. Казачьей и Соленой, обусловленные взаимным влиянием бухт.
N o te . Values for the basin with parabolic bottom profile are given in brackets. Periods with good agreement are highlighted in bold. The periods in Kazachya and Solyonaya Bays, resulting from their interaction, are underlined.
На рис. 5–8 показаны пространственные распределения спектральной плотности энергии, приходящейся на единицу времени, основных энергоне- сущих колебаний уровня в б. Стрелецкой, Круглой, Камышовой, Двойной, рассчитанные по формуле (5). Для б. Стрелецкой (рис. 5) максимальные значения спектральной плотности энергии сейшевых колебаний уровня от- мечаются в районе восточного побережья бухты и в ее вершине (ст. 3 и 5). В б. Круглой (рис. 6) основная часть энергии сейшевых колебаний сосредо- точена в ее вершине (ст. 8). На рис. 7 показано пространственное распределе- ние спектральной плотности энергии для б. Камышовой, откуда видно, что наиболее интенсивные колебания характерны для узкой части бухты вблизи вершины (ст. 12–14). Наиболее сложная энергетическая картина получена в случае б. Двойной (рис. 8). Видно, что резонансные свойства бухты, кото- рая состоит из двух рукавов, проявляются в интенсификации колебаний уровня как в восточном рукаве – б. Казачьей, так и в западном – б. Соленой. Согласно аналитическим оценкам (таблица), моды 5.1, 17.1 и 2.7 мин явля- ются собственными периодами б. Казачьей (восточный рукав б. Двойной), поэтому максимальные значения спектральной плотности энергии для этих периодов отмечаются в этой бухте (рис. 8, а, b, d). Мода с периодом, равным
6.7 мин, согласно расчетам, также заметно выражена в б. Казачьей (рис. 8, c).
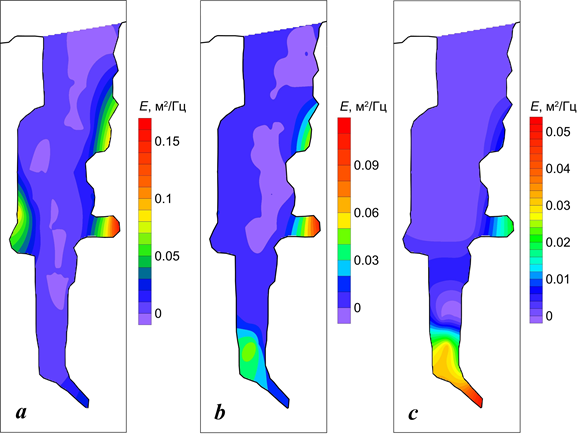
Р ис . 5 . Пространственное распределение спектральной плотности основных энергонесущих колебаний уровня в б. Стрелецкой для периода Т, равного 1.3 мин (а), 1.6 мин (b), 2.8 мин (c)
F i g. 5. Spatial distribution of spectral density of main energy- carrying level oscillations in Streletskaya Bay for a period T of 1.3 min (а), 1.6 min (b), 2.8 min (c)
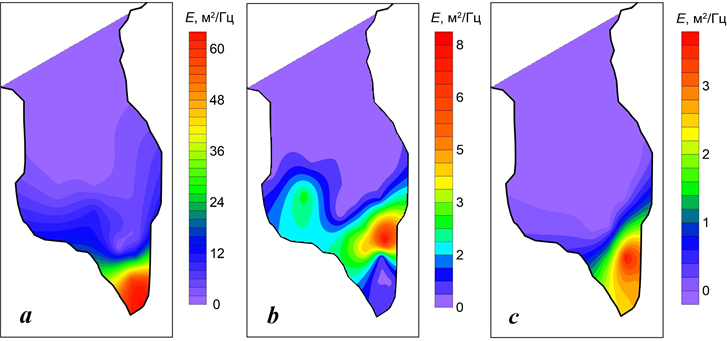
Р ис . 6 . Пространственное распределение спектральной плотности основных энергонесущих колебаний уровня в б. Круглой для периода Т, равного 4.6 мин (а), 2.7 мин (b), 10.6 мин (c)
F i g. 6. Spatial distribution of spectral density of main energy-carrying level oscillations in Kruglaya Bay for a period T of 4.6 min (а), 2.7 min (b),
10.6 min (c)
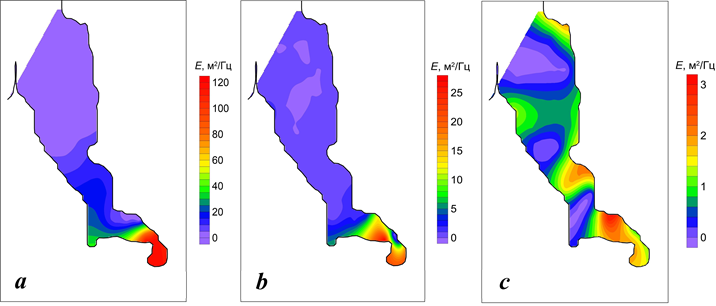
Р ис . 7 . Пространственное распределение спектральной плотности ос- новных энергонесущих колебаний уровня в б. Камышовой для периода Т, равного 7.1 мин (а), 1.5 мин (b), 3.6 мин (c)
F i g. 7. Spatial distribution of spectral density of main energy-carrying lev- el oscillations in Kamyshovaya Bay for a period T of 7.1 min (а), 1.5 min (b),
3.6 min (c)
Наибольшие значения спектральной плотности энергии для периодов 2.0 и
9.5 мин получены в б. Соленой, поскольку они являются собственными пери- одами б. Соленой (западного рукава б. Двойной) (рис. 8, e, f).
Анализ результатов расчета показал, что наибольшие значения спек- тральной плотности энергии колебаний уровня характерны для б. Казачьей (рис. 8), где спектральная плотность составила свыше 150 м2/Гц для периода
5.1 мин, и в б. Камышовой – около 120 м2/Гц для периода 7.1 мин. В б. Круг- лой максимальная спектральная плотность составила около 65 м2/Гц для пе- риода 4.6 мин; наименьшие значения спектральной плотности энергии отме- чены в б. Стрелецкой (около 0.15 м2/Гц для периода 1.3 мин).
На рис. 9 показано пространственное распределение относительных (приведенных к максимальному значению) амплитуд сейшевых колебаний уровня моря в бухтах. Видно, что наибольшие значения амплитуд приходятся в основном на вершины бухт, кроме б. Стрелецкой, в которой доминирует поперечная мода.
Приведенные на рис. 5–9 пространственные распределения амплитуд и спектральной плотности колебаний уровня могут быть полезны для выяв- ления локальных зон, в которых возможны значительные подъемы уровня, вызванные сейшами, что важно при обеспечении безопасности портов и дру- гих объектов инфраструктуры, расположенных на побережьях бухт.
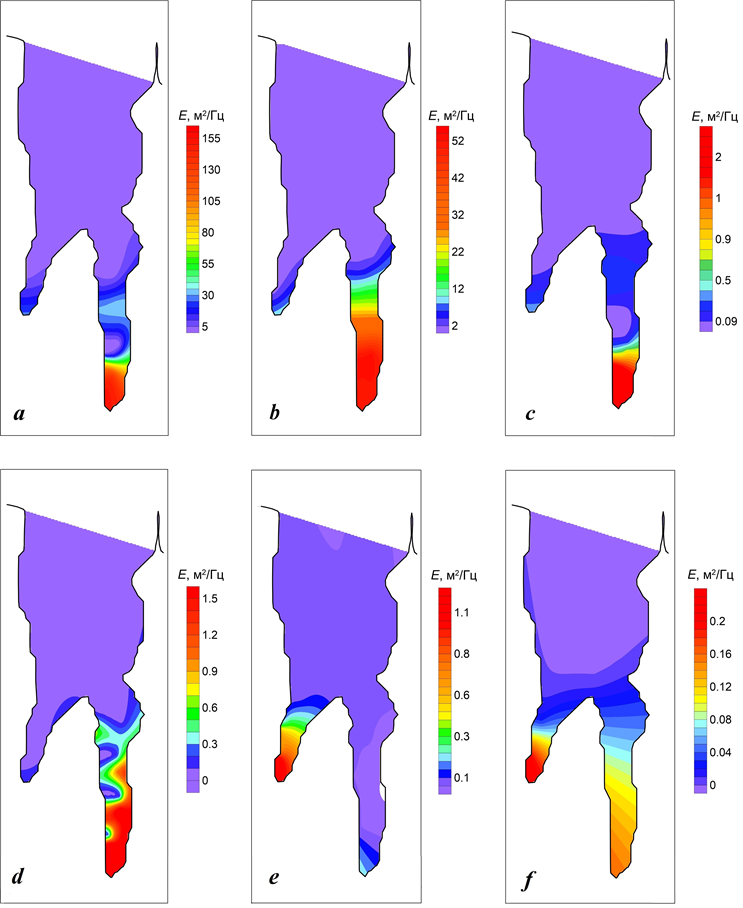
Р ис . 8 . Пространственное распределение спектральной плотности ос- новных энергонесущих колебаний уровня в б. Двойной для периода Т, равного 5.1 мин (а), 17.1 мин (b), 6.7 мин (c), 2.7 мин (d), 2.0 мин (e),
9.5 мин (f)
F ig . 8 . Spatial distribution of spectral density of main energy-carrying level oscillations in Dvoynaya Bay for a period T of 5.1 min (а), 17.1 min (b), 6.7 min (c), 2.7 min (d), 2.0 min (e), 9.5 min (f)
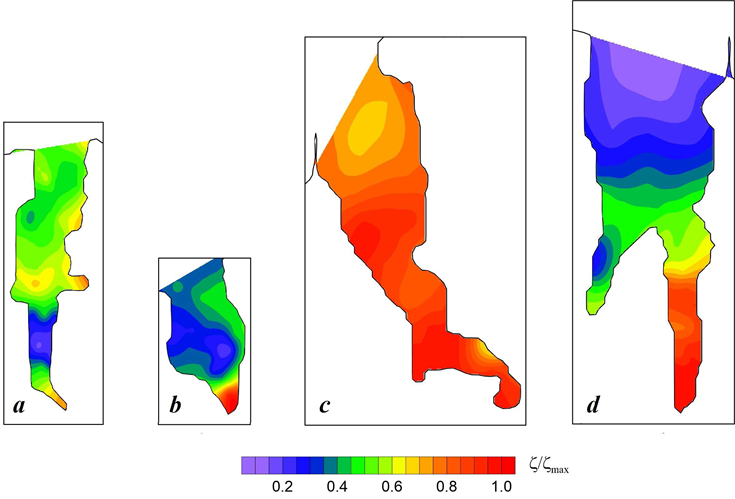
Р ис . 9 . Пространственное распределение относительных амплитуд сейшевых колебаний уровня в севастопольских бухтах: а – Стрелецкой; b – Круглой; c – Ка- мышовой; d – Двойной
F i g . 9 . Spatial distribution of relative amplitudes of level seiche oscillations in Sevas- topol bays: а – Streletskaya; b – Kruglaya; c – Kamyshovaya; d – Dvoynaya
Заключение
На основе гидродинамической численной модели ADCIRC исследованы резонансные свойства севастопольских бухт: Стрелецкой, Круглой, Камы- шовой, Двойной, включающей в себя б. Казачью и Соленую. Расчеты вы- полнены для акватории каждой бухты отдельно. В качестве возмущения ис- пользован «красный шум». Определены резонансные периоды указанных бухт и пространственное распределение спектральной плотности энергии колеба- ний уровня по акватории бухт. Для контроля значений резонансных периодов использованы аналитические оценки. На основе анализа результатов выпол- ненных расчетов можно сделать следующие выводы.
Большинство выделенных резонансных периодов для севастопольских бухт удовлетворительно согласуются с аналитическими оценками этих пери- одов. Лишь в б. Стрелецкой не удалось возбудить воздействием «красного шума» моду Гельмгольца, период которой, по аналитическим оценкам, состав- ляет около 13.5 мин. Период старшей резонансной моды б. Камышовой ока- зался равным 12.9 мин, что значительно отличается от аналитической оценки (19.8 мин). Это связано с тем, что акватория бухты имеет сложную простран- ственную структуру, а на входе в нее сооружены два защитных мола.
Использование при моделировании батиметрических данных и профилей береговой черты, приближенных к реальным, позволило определить допол- нительные резонансные периоды для всех рассмотренных бухт, которые нельзя получить при аналитических оценках.
В б. Двойной, включающей в себя б. Казачью и Соленую, обнаружено расширение спектрального состава резонансных мод, возникающее из-за свя- зи этих бухт через их входы.
Анализ пространственного распределения спектральной плотности ос- новных энергонесущих колебаний уровня в б. Стрелецкой, Круглой, Камы- шовой и Двойной показал, что ее максимальные значения отмечаются в ос- новном в вершинах бухт. В б. Двойной максимальные значения спектральной плотности проявляются в восточном или западном рукавах (б. Казачьей или Соленой соответственно) в зависимости от того, к какому из рукавов отно- сится собственный период.
Для уточнения резонансных свойств севастопольских бухт требуется проведение натурных наблюдений в бухтах системы.
Результаты исследования могут быть использованы при проектировании размещения гидротехнических сооружений, развитии марикультуры, плани- ровании выпусков сточных вод и т. п.
1. Манилюк Ю. В., Лазоренко Д. И., Фомин В. В. Сейшевые колебания в системе Се- вастопольских бухт // Водные ресурсы. 2021. T. 48, № 5. С. 526–536. EDN LZQQZR. https://doi.org/10.31857/S0321059621050126
2. Рабинович А. Б. Длинные гравитационные волны в океане: захват, резонанс, из- лучение. Санкт-Петербург : Гидрометеоиздат, 1993. 325 с.
3. Алексеев Д. В., Манилюк Ю. В., Санников В. Ф. Сейшевые течения в бассейне с открытым входом // Прикладные задачи математики : материалы XXV между- народной научно-технической конференции. Севастополь, 2017. С. 109–115. EDN YKYDCA.
4. Доценко С. Ф., Иванов В. А. Природные катастрофы Азово-Черноморского реги- она. Севастополь : ЭКОСИ-Гидрофизика, 2010. 174 с.
5. Coupling between two inlets: Оbservation and modeling / P. L.-F. Liu [et al.] // Journal of Geophysical Research: Oceans. 2003. Vol. 108, iss. C3. 3069. https://doi.org/10.1029/2002JC001478
6. Манилюк Ю. В., Лазоренко Д. И., Фомин В. В. Исследование сейшевых колебаний в смежных бухтах на примере Севастопольской и Карантинной бухт // Морской гидрофизический журнал. 2020. Т. 36, № 3. С. 261–276. EDN QEFCWJ. https://doi.org/10.22449/0233-7584-2020-3-261-276
7. Фомичева Л. А., Рабинович А. Б., Демидов А. Н. Уровень моря // Гидрометеороло- гия и гидрохимия морей СССР. Ленинград : Гидрометеоиздат, 1991. Т. IV : Черное море, вып. 1 : Гидрометеорологические условия. С. 329–354. (Проект «Моря СССР»).
8. Течения в Севастопольской бухте по данным ADCP-наблюдений (июнь 2008 года) / А. Н. Морозов [и др.] // Морской гидрофизический журнал. 2012. № 3. С. 31–43. EDN TMJXDX.
9. Medvedev I. P. Tides in the Black Sea: observations and numerical modelling // Pure and Applied Geophysics. 2018. Vol. 175, iss. 6. P. 1951–1969. https://doi.org/10.1007/s00024- 018-1878-x
10. Сейши в Севастопольской бухте / Ю. Н. Горячкин [и др.] // Труды УкрНИГМИ. 2002. Вып. 250. С. 342–353.
11. Sea level oscillations spectra of a shallow coastal bay: Cost-effective measurements and numerical modelling in Kruglaya Bay / Yu. V. Manilyuk [et al.] // Regional Studies in Marine Science. 2024. Vol. 69. 103326. https://doi.org/10.1016/j.rsma.2023.103326
12. Study of Seiche Oscillation Regimes in Sevastopol Bay / Yu. V. Manilyuk [et al.] // Oceanology. 2023. Vol. 63, iss. 6. P. 796–805. EDN TUCTSH. https://doi.org/10.1134/s0001437023060115
13. Балинец Н. А., Хмара Т. В. Явление тягуна в бухтах Севастополя // Экологическая безопасность прибрежной и шельфовой зон и комплексное исследование ресурсов шельфа. 2006. Вып. 14. С. 204–208. EDN ZBOAIB.
14. Фомин В. В., Лазоренко Д. И., Иванча Е. В. Численное моделирование сейш в Ба- лаклавской бухте // Экологическая безопасность прибрежной и шельфовой зон моря. 2017. № 3. С. 32–39. EDN ZMZFVV.
15. Рабинович А. Б., Монсеррат С., Файн И. В. Численное моделирование экстре- мальных сейшевых колебаний в районе Балеарских островов // Океанология. 1999. Т. 39, № 1. С. 16–24.
16. Belokon A. Y., Lazorenko D. I. Energy spectra of sea level fluctuations during propaga- tion long waves in branched bays // Proceedings of the 9th International Conference on Physical and Mathematical Modelling of Earth and Environmental Processes 2023. Cham : Springer, 2024. P. 471–484. (Springer Proceedings in Earth and Environmen- tal Sciences). https://doi.org/10.1007/978-3-031-54589-4_49
17. Иванов В. А., Манилюк Ю. В., Санников В. Ф. Сейши в бассейне с открытым вхо- дом // Прикладная механика и техническая физика. 2018. Т. 59, № 4. С. 23–30. EDN XTUVKX. https://doi.org/10.15372/PMTF20180404