Введение

Наиболее эффективным средством мониторинга водной среды при любых метеорологических условиях и в любое время суток являются радиолокационные (РЛ) системы. В настоящее время разработаны алгоритмы, которые по спутниковой РЛ информации позволяют определить скорость и направление ветра, характеристики поверхностного волнения, исследовать вихри и фронтальные разделы (см., например, [1, 2] и цитируемую в этих работах литературу). Данные методики обработки данных базируются на развитых теоретических моделях формирования отраженного от морской поверхности РЛ сигнала при углах наблюдения поверхности от 15 до 60° [3].

Однако по спутниковым данным невозможно проводить непрерывный мониторинг полей скорости ветра, течений и характеристик поверхностного волнения в портах, прибрежных акваториях и районах интенсивного судоходства. Для оперативного и непрерывного мониторинга выбранного района используются навигационные радиолокационные станции (РЛС), устанавливаемые на морских платформах, судах или на береговых сооружениях. Для анализа данных РЛС разработаны и апробированы методики восстановления скорости и направления поверхностных течений, определения характеристик поверхностного волнения (см., например, [4–6] и цитируемую в этих работах литературу).

Восстановление скорости ветра по РЛ изображениям в основном базируется на эмпирических моделях, которые устанавливают взаимосвязь между интенсивностью РЛ сигнала и модулем скорости ветра U. В работе [7] предложено использовать геофизическую модельную функцию (ГМФ) третьего порядка. При скоростях ветра ~ 4 и 22 м/с ошибки восстановления скорости составили ~ 0.8 и ~ 0.1 м/с соответственно. Для определения направления скорости ветра интенсивность РЛ сигнала, в зависимости от азимута наблюдения морской поверхности j, аппроксимируется гармонической функцией [8]. Значение угла, при котором наблюдается максимальное значение РЛ сигнала, принимается за направление ветра j_U. Для определения U в [8] предложена эмпирическая модельная функция, в которой использовался РЛ сигнал, проинтегрированный по всем азимутальным углам. Другим способом восстановления вектора скорости ветра по изображениям морского навигационного радара является использование нейронных сетей [9].

К сожалению, во многих работах, описывающих алгоритмы восстановления поля ветра по данным береговых или судовых РЛС, не приводятся информация о линейности характеристик приемного тракта радиолокационной станции и ее калибровочные зависимости. В результате не представляется возможным пересчитать интенсивность сигнала в удельную эффективную площадь рассеяния (УЭПР) s₀ и провести сопоставление с данными из других источников и теоретическими моделями. Перечисленные выше эмпирические ГМФ не базируются на физических представлениях о формировании радиосигнала, отраженного от морской поверхности при больших углах зондирования. При этом применяются различные методы сглаживания и фильтрации исходного сигнала, что затрудняет использование предложенных методик для других типов радаров.

Береговые или судовые РЛС работают, как правило, на горизонтальной поляризации излучения/приема сигнала при углах зондирования морской поверхности 75–89°. Для таких условий наблюдений основной вклад в формирование УЭПР вносят обрушения ветровых волн [1, 3, 10–12]. В современных моделях s₀ зависит от доли поверхности моря q, занятой обрушениями. Соответственно, изменения УЭПР при изменении скорости ветра должны быть связаны с ветровой зависимостью q. В то же время q зависит от возраста волн [13–15], что приводит к изменению уровня s₀ при одинаковом ветре, но разном возрасте ветровых волн.

Учет физического состояния морской поверхности является особенно важным для восстановления параметров атмосферы в прибрежной акватории, где в зависимости от направления ветра степень развития ветровых волн изменяется в широких пределах.

Целью работы является построение полуэмпирической модели ветровой зависимости УЭПР морской поверхности в Х-диапазоне при горизонтальной поляризации излучения/приема сигнала при больших углах падения в широком диапазоне возраста ветровых волн.

Место проведения эксперимента и аппаратура

Натурный эксперимент проводился в августе – октябре 2022–2024 гг. на стационарной океанографической платформе, расположенной в Голубом заливе в районе пос. Кацивели, Южный берег Крыма (рис. 1, а). Стационарная океанографическая платформа установлена в ~ 480 м от ближайшей точки берега и имеет координаты 44°23ʹ38ʹʹ с. ш., 33°59ʹ09ʹʹ в. д. Глубина в месте проведения измерений составляет около 30 м.

При измерениях использовали РЛС MRS-1011 (производитель АО НПФ «Микран», г. Томск) ближнего обзора с высоким разрешением по дальности (Dl = 0.79 м), работающую на горизонтальной поляризации передачи/приема сигнала. Мощность радиолокатора составляет не более 1 Вт, ширина диаграммы направленности в горизонтальной плоскости (Dj = 1°, в вертикальной плоскости – 30°). В данной РЛС формируется непрерывный линейно модулируемый сигнал на рабочей частоте 9430 МГц (длина волны l_r = 3.2 см), модулированный периодической пилообразной функцией с периодом 7 мс. Ширина полосы зондирующего сигнала составляет 200 МГц относительно рабочей частоты. Принимаемый отраженный сигнал подвергается усилению и гомодинной обработке. В результате формируется сигнал биений, спектр которого отображает дальность и эффективную площадь рассеяния s (ЭПР) цели.

Радиолокатор устанавливался на океанографической платформе на высоте 15 м над уровнем моря (рис. 1, b, c) и во время эксперимента использовался в режиме кругового обзора с угловой скоростью вращения антенны 2.79 рад/с. Из-за особенностей расположения станции на платформе сектор обзора морской поверхности находился в пределах от 55° до 315° географического азимута.

В качестве примера на врезке рис. 1, а представлено РЛ изображение морской поверхности, на котором отчетливо видны поверхностные волны. Яркая область в верхней левой части связана с отражениями РЛ сигнала от берега. Темный участок является следствием затенения элементами платформы, в данном секторе передатчик РЛС не включался.

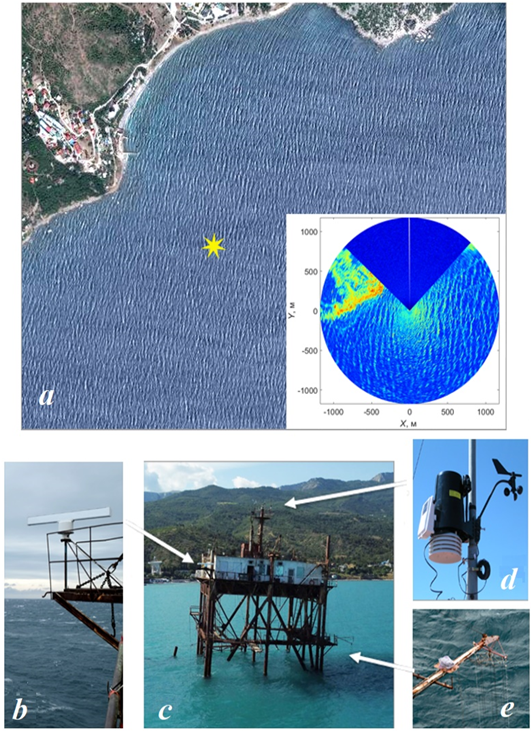
Рис. 1. Район проведения исследований (a) и используемое оборудование. Звездочкой отмечено расположение стационарной океанографической платформы; на врезке представлено радиолокационное изображение морской поверхности; b – радиолокационная станция MRS‑1011; c – стационарная океанографическая платформа, стрелками отмечены места размещения приборов, показанных на рисунках b, d, e; d – метеостанция; e – струнный волнограф

Fig. 1. Study area (a) and equipment used. The star indicates the location of the stationary oceanographic platform; the inset shows a radar image of the sea surface; b – MRS-1011 radar station; c – stationary oceanographic platform, the arrows indicate the location of the equipment shown in b, d, e; d – meteorological station; e – string wave recorder

Скорость и направление ветра, атмосферное давление, температура воздуха и влажность регистрировали с помощью метеостанции Davis Vantage Pro2 6152, расположенной на высоте 23 м над уровнем моря на мачте океанографической платформы (рис. 1, d). Температура воды измерялась на глубине 3 м.

Расчет скорости ветра на горизонте 10 м для нейтральной стратификации атмосферного пограничного слоя был выполнен с использованием метеорологических данных и данных о температуре приповерхностной воды по методике COARE 3.0 из работы [16].

Характеристики поверхностного волнения регистрировали с помощью струнного волнографа (рис. 1, e). В результате обработки волнографических данных получены частотные спектры возвышений морской поверхности S(f). Как правило, при проведении наших измерений помимо ветровых волн присутствовали волны зыби. Для разделения частотного спектра волнения на волны зыби и волны, генерируемые ветром, использовали подход [17]. В результате были определены значения частоты спектрального пика f_p, частоты пика ветрового волнения f_pw, а также возраст ветровых волн a = c_pw/U, где
c_pw – фазовая скорость волн на частоте пика ветровых волн.

Геометрические характеристики обрушений ветровых волн определяли по видеозаписям морской поверхности, выполненных с помощью цифровой видеокамеры. Дополнительная информация об алгоритме и расчете различных параметров обрушений приведена в работах [18, 19].

Гистограммы измеренных в эксперименте значений U, j_U и a приведены на рис. 2. Как следует из рис. 2, a, скорость ветра варьировалась от 2
до 20 м/с, при этом основное число наблюдений выполнялось в диапазоне U от 5 до 15 м/с. Во время проведения работ наблюдались преимущественно восточные (j_U = 60–120°) и западные (j_U = 250°) ветры (рис. 2, b). Распределение возраста волн, представленное на рис. 2, c, показывает, что α изменялось от 0.1 до 3, при этом ~ 96 % значений возраста волн лежало в пределах 0.1–1.2.

Из дальнейшей обработки были исключены случаи, когда на море преобладала зыбь. Вызванные зыбью сильные модуляции радиолокационного сигнала могут существенно повлиять на средние значения s₀, но не являются предметом исследования в статье.

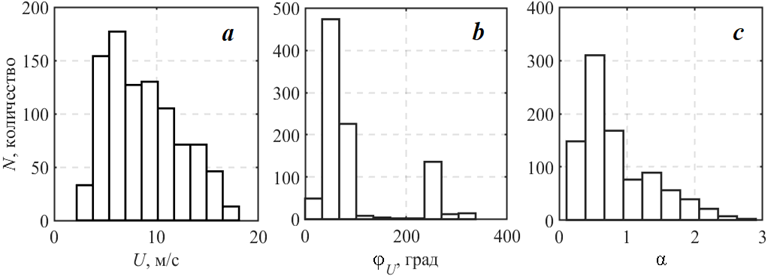
Рис. 2. Гистограммы ветровых и волновых условий измерений: a – скорости ветра; b – направления ветра; c – возраста волн

Fig. 2. Histograms of wind and wave measurement conditions: a – wind speed; b – wind direction; c – wave age

Предварительная обработка данных

В работе использовали радиолокатор, аналогичный по своим техническим характеристикам РЛС, используемой в [20], но с увеличенной мощностью передатчика.

Для перевода условных единиц РЛ сигнала в абсолютные величины УЭПР s₀ была выполнена калибровка РЛС. В качестве мишени использовали надувной шар из полимера (толщина стенки ~ 1 мм, диаметр D_Ball = 67.5 см) с добавлением алюминиевой пудры. Для придания проводящих свойств шар дополнительно покрывали краской с добавлением алюминиевой пудры. Учитывая, что l_r << D_Ball /2, ЭПР шара составляет s_Ball = 0.36 м². В штилевую погоду мишень буксировали надувной лодкой на расстояние до 1000 м от платформы.

Проведение калибровочных работ необходимо, поскольку полученные значения облегчают интерпретацию данных, так как модели РЛ рассеяния оперируют абсолютными значениями сигнала. Отметим, что калибровочные константы для разных устройств разные.

Как было показано в работе [20], характеристики приемника используемой нами РЛС являются нелинейными. Соответственно, следует ожидать, что принимаемая мощность сигнала от шара P_R не будет описываться основной радиолокационной формулой. На рис. 3 представлена зависимость величины P_R/s_Ball от расстояния до шара R. Данные измерений могут быть описаны степенной функцией вида 

P_R / s_Ball = C×R^–d,                                            (1)

где коэффициенты C = 1.1×10¹² и d = 3.4 получены методом наименьших квадратов.

Величина отраженного сигнала, рассеянного морем, зависит от значения площади облучаемого участка морской поверхности S. Для исключения этого влияния сигнал, отраженный от морской поверхности, описывают как УЭПР s₀ = s / S, где S = 2Dl R tan(Dj/2).

С учетом калибровочных констант УЭПР морской поверхности для всех точек РЛ изображения определялась как

s₀ = C ¢PR^2.4,

где C ¢ = 1/[2C Dl tan(Dj/2)]; P – мощность принимаемого РЛ сигнала.

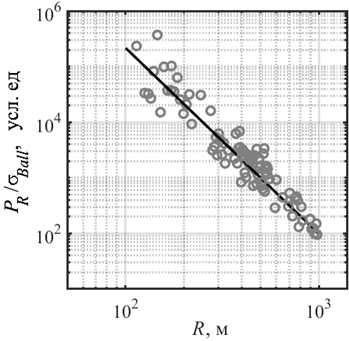
Рис. 3. Зависимость мощности принимаемого сигнала, нормированного на ЭПР шара, от расстояния до цели. Прямой показана аппроксимация степенной функцией (1)

Fig. 3. Dependence of the received signal power normalised to the ball radar cross-section on the distance to the target. The straight line shows approximation by power function (1)

Модель небрегговской компоненты рассеяния

В работе [3] рассматривается модель формирования РЛ УЭПР морской поверхности. В общем случае s₀ может быть представлена в виде суммы брегговской s_0br и небрегговской s_0nb компонент рассеяния

s₀ = s_0br (1 – q) + s_0nb q.

Согласно [3], s_0nb формируется в условиях квазизеркальных отражений от очень шероховатых участков зоны обрушения, и тогда УЭПР барашка запишется как

s_0nb(q, j) =s_0wb(1 + M_wb q_wb A_wb(j)),                            (2)

s_0nb(q) = (sec⁴(q)/s_wb²) exp(–tan²(q)/s_wb²) + s_wb/s_wb²,                (3)

где q – угол падения, отсчитываемый от надира; j – азимут наблюдения РЛ станции; M_wb – модуляционная передаточная функция; q_wb – средний наклон барашка; A_wb(j) – коэффициент, определяющий угловое распределение небрегговского рассеяния и обеспечивающий разницу между РЛ сигналами при наблюдениях «на ветер» и «по ветру»; e_wb² – среднеквадратичный уклон шероховатостей зоны обрушения; e_wb – константа, равная отношению толщины барашка к его длине. При больших углах падения (q > 75°) [21] основной вклад в РЛ сигнал на горизонтальной поляризации вносит s_0nb , а определяющую роль в выражении (3) играет второе слагаемое и, следовательно, s₀ с учетом (2) может быть записана как

s₀ = (s_wb/s_wb²) (1 + M_wb q_wb A_wb(j)) q,                            (4)

Согласно выражению (4), s₀ не должна зависеть от угла наблюдения морской поверхности. Для совсем больших углов (q > 88–89°) на величину УЭПР могут оказывать влияние эффекты, связанные с затенением участков морской поверхности гребнями длинных волн. Как следует из формулы (4), изменение мощности сигнала будет определяться долей морской поверхности, покрытой обрушениями ветровых волн.

Традиционно q описывается степенной функцией q = B₀Uⁿ (см., например, [19, 22–24]). Однако большой разброс данных [13, 14] указывает на то, что скорость ветра сама по себе не объясняет всей наблюдаемой изменчивости q. В частности, согласно [13–15], коэффициент B₀ является функцией возраста волн B₀ = f(a). Поскольку функция f(a) может быть нелинейной, зададим ее в виде степенной функции f(a) = a^b. Из сказанного выше следует выражение общего вида, являющееся аналогом ГМФ:

s₀(j, q) = B(j, q) a ^{b(j, q)} U ^{n(j, q)},                                (5)

где b(j, q), n(j, q) и B(j, q) – константы.

Отметим, что, поскольку наши данные получены в условиях, близких к нейтральной стратификации атмосферы, проявлением эффектов стратификации на обрушения волн будем пренебрегать.

Рис. 4. УЭПР морской поверхности как функция угла наблюдения при измерениях «на ветер» (a), «перпендикулярно ветру» (b) и «по ветру» (c). Синяя линия – данные, усредненные в диапазоне U = 7.0 ± 1.5 м/с; красная – 11.0 ± 1.5 м/с; оранжевая – 15.0 ± 1.5 м/с. Доверительные интервалы приведены в левой нижней части рисунка

Fig. 4. Normalized radar cross-section (NRCS) of the sea surface as a function of the angle of observation for ‘up-wind’ (a), ‘perpendicular to the wind’ (b) and ‘down-wind’ (c) measurements. The blue line is data averaged over the range U = 7.0 ± 1.5 m/s; the red line is 11.0 ± 1.5 m/s; the orange line is 15.0 ± 1.5 m/s. Confidence intervals are given in the bottom left part of the figure

Анализ полученных данных

Угловые зависимости радиолокационного сигнала

Зависимость УЭПР от угла падения при наблюдениях «на ветер» s₀^up «перпендикулярно ветру» s₀^cr и «по ветру» s₀^dw представлена на рис. 4. Среднеквадратичное отклонение, осредненное по реализациям, не превышало 5 дБ. Как видно из рис. 4, УЭПР морской поверхности для углов падения 83.5 £ q £ 88° почти не меняется, а при бóльших значениях q УЭПР снижается вследствие влияния затенений гребнями длинных волн. Для построения ГМФ с целью восстановления вектора скорости ветра будем рассматривать среднее значение s₀ в диапазоне углов (83.5–88°) и на ниспадающем участке s₀ для значений q, равных 88 и 89°. Для наших условий наблюдения это соответствует расстоянию 130–860 м.

Ветровые зависимости радиолокационного сигнала

На рис. 5 приведен пример ветровых зависимостей s₀^up, s₀^cr, s₀^dw для диапазона углов 83.5 £ q £ 88°. Как следует из рис. 5, наблюдается степенная зависимость s₀ от скорости ветра. Отметим, что при одной и той же скорости ветра на уровне измерений с увеличением a, то есть в процессе развития волнения, значения s₀ увеличиваются. Данная закономерность характерна для всех выбранных азимутов наблюдения. При изменении a от 0.1 до 1.2 наиболее слабый рост s₀ приблизительно в 5 раз наблюдается для s₀^up, а наибольшее увеличение УЭПР в ~ 30 раз характерно для s₀^cr. Полученная зависимость s₀ от скорости ветра и возраста волн подтверждает целесообразность описания УЭПР морской поверхности в виде выражения (5).

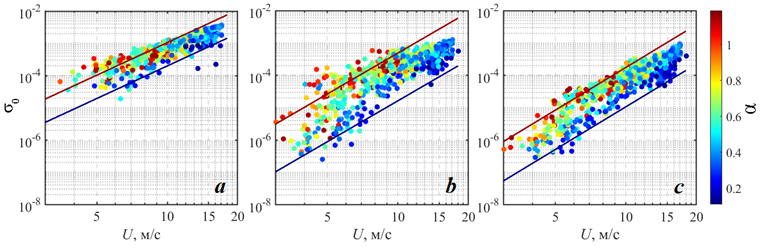
Рис. 5. УЭПР морской поверхности как функция скорости ветра при зондировании «на ветер» (a), «перпендикулярно ветру» (b) и «по ветру» (с). Сплошные линии соответствуют зависимости (5) с коэффициентами, приведенными в таблице для a = 0.1 (синяя линия) и a = 1.2 (красная линия)

Fig. 5. NRCS of the sea surface as a function of wind speed during ‘up-wind’ (a), ‘perpendicular to the wind’ (b) and ‘down-wind’ (c) sensing. The solid lines correspond to dependency (5) with coefficients given in the table for a = 0.1 (blue line) and a = 1.2 (red line)

Коэффициенты ветровой зависимости УЭПР

Coefficients of NRCS wind dependency

Приведенные в таблице значения коэффициентов B, b, n для различных значений q и азимутов в интервале 0.1 £ a £ 1.2 определялись методом наименьших квадратов по экспериментальным массивам одновременных измерений скорости ветра, возраста волн и s₀(j, q). При направлении «на ветер» для указанных углов падения q значения соответствующих степеней почти одинаковы. Уменьшение уровня B при углах наблюдения q ³ 88.5° можно объяснить условиями затенения.

Полученные значения n попадают в известный по работам [14, 25, 26] диапазон оценок ветрового коэффициента для доли морской поверхности, покрытой обрушениями.

Рассмотренная выше модель УЭПР при больших углах падения (4) указывает, что s₀ определяется значением q. Следовательно, ветровая зависимость s₀ должна определяться зависимостью q от U. Отметим, что в s₀ = f(U) могут участвовать первые два сомножителя в правой части выражения (4), содержащие s_wb², M_wb, q_wb, однако их значения мы не определяли. Воспользуемся архивными данными q и полученными одновременно при измерениях в эксперименте значениями s₀ и q.

Рис. 6. Доли поверхности, покрытой обрушениями, и УЭПР: a – ветровые зависимости q и s₀ (  – значения s₀^up при U = 2.2¸17.1 м/с,  – значения q при U = 4.7¸21.4 м/с); b – зависимость УЭПР от q, полученная при синхронных измерениях

Fig. 6. Fractions of the whitecap coverage and NRCS: a – wind dependencies q and s₀; (  – values of s₀^up at U = 2.2¸17.1 m/s,
 – values of q at U = 4.7¸21.4 m/s) b – dependency of NRCS on q derived from synchronous measurements

Обе ветровые зависимости почти совпадают, однако незначительное различие наблюдается при U < 10 м/с, в этих случаях с уменьшением ветра начинается более сильное уменьшение величины q. Это можно объяснить тем, что при умеренных и слабых ветрах небольшие обрушения, вносящие существенный вклад в величину q, при обработке видеозаписей не идентифицируются [27, 28]. В то же время такие обрушения участвуют в формировании УЭПР.

Интерес представляет сопоставление s₀ и доли поверхности, покрытой активной фазой обрушений. Действительно, в соответствии с моделью (4) должно наблюдаться простое соотношение s₀ µ q. На рис. 6, b демонстрируется зависимость УЭПР от q, полученная по нашим данным в результате синхронных измерений. Как следует из рис. 6, b, зависимость УЭПР от q удовлетворительно описывается линейной функцией, показанной сплошной линией s₀ = 1.47q. Такая линейная зависимость подтверждает модель (4) формирования УЭПР при больших углах падения РЛ сигнала.

Азимутальные зависимости радиолокационного сигнала

Предыдущие исследования [29–31] показали, что для морских навигационных станций, работающих на горизонтальной поляризации сигнала при q > 75°, максимальное значение РЛ сигнала наблюдается в направлении «на ветер». Для описания азимутальной зависимости сигнала и нахождения скорости и направления ветра аппроксимируем наши данные стандартной зависимостью в виде ограниченного ряда Фурье (см. например, [32])

s(U, j, q) = A₀ + A₁ cos(j – j_w) + A₂ cos[2(j – j_w)],                 (6)

где j_w – направление максимума азимутальной зависимости; A₀, A₁, A₂ – коэффициенты, которые в общем случае зависят от U, a, q и записываются согласно работе ^[1]) как

A₀ = (s₀^up + s₀^cr + s₀^dw)/4,                                  (7)

A₁ = (s₀^up – s₀^dw)/2,                                       (8)

A₂ = (s₀^up – 2s₀^cr + s₀^dw)/4.                                 (9)

В наших обозначениях направление j = j_w соответствует измерениям «на ветер», j = j_w + p – «по ветру». В формулах (7)–(9) s₀^up, s₀^cr, s₀^dw описываются выражением (6), значения коэффициентов B, b, n приведены в таблице. На рис. 7 демонстрируются азимутальные зависимости УЭПР для восточного и западного направления ветра. Линией показана зависимость (6) с учетом выражений (5) и (7)–(9). Неизвестными в формуле (6) являются U_RL и j_w, которые определяли методом наименьших квадратов (при U_RL = 10 м/с, j_w = 80° для линии на рис. 7, a и при U_RL = 14 м/с, j_w = 250° для линии на рис. 7, b). Возраст волн при проведении РЛ измерений рассчитывали по спектрам возвышений ветровых волн.

При умеренных скоростях ветра (рис. 7, а) азимутальная зависимость s₀(j) имеет один явно выраженный максимум при измерениях «на ветер», минимальное значение наблюдается «по ветру». При усилении скорости ветра (рис. 7, b) азимутальная зависимость приобретает двухмодальный характер, появляется второй локальный максимум в направлении «по ветру». Особенности азимутальных зависимостей при больших углах наблюдения поверхности моря более подробно рассмотрены в [20].

Скорости U_RL и j_w для всей совокупности данных рассчитывались методом наименьших квадратов по формуле (6) с использованием натурных РЛ измерений. На рис. 8 сопоставляются направление и модуль скорости ветра, восстановленные по РЛ данным, с измеренными анемометром.

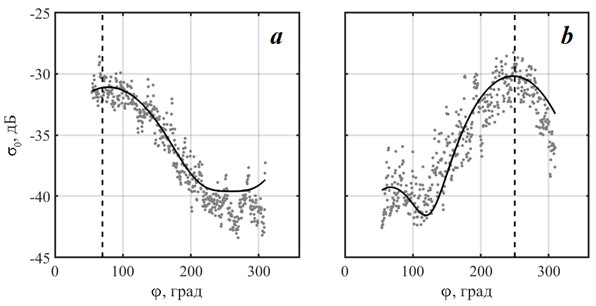
Рис. 7. УЭПР морской поверхности как функция азимутального угла при значениях U = 9 м/с, j_U = 70°, a = 0.8 (a); U = 15 м/с, j_U = 250°, a = 0.2 (b). Штриховые линии обозначают направление ветра по измерениям анемометра

Fig. 7. The sea surface NRCS as an azimuth angle function at U = 9 m/s, j_U = 70°, a = 0.8 (a); U = 15 m/s, j_U = 250°, a = 0.2 (b). The dashed lines are for wind direction retrieved from the anemometer data

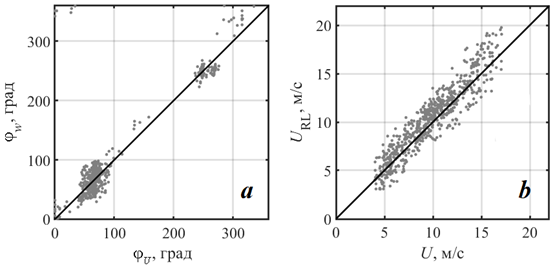
Рис. 8. Направление (а) и модуль скорости ветра (b), полученные по данным анемометра и РЛ измерениям. Прямая линия соответствует равным значениям двух величин

Fig. 8. Wind speed direction (a) and vector magnitude (b) retrieved from the anemometer and radar data. The straight line corresponds to equal values of the two quantities

Как следует из рис. 8, наблюдается линейная связь как между j_w и j_U, так и между U_RL и U, при этом среднеквадратичные отклонения между указанными парами величин составляют соответственно 30° и 1.2 м/с.

Выводы

Предложена полуэмпирическая модель ветровой зависимости УЭПР морской поверхности, позволяющая восстанавливать приводную скорость ветра при РЛ зондировании морской поверхности в Х диапазоне под большими углами падения. Для анализа использовали радиолокационные, метеорологические, волнографические данные и видеозаписи морской поверхности, полученные в 2022–2024 гг. на стационарной океанографической платформе в Голубом заливе, Южный берег Крыма. Измерения проводили при скорости ветра от 4 до 17 м/с. Наблюдаемый возраст волн изменялся от 0.1 до 3, при этом 96 % значений a находилось в интервале 0.1 £ a £ 1.2.

При РЛ зондировании моря под большими углами падения доля поверхности моря q, покрытая обрушениями, является основным информативным параметром, формирующим УЭПР s₀. Зависимость покрытой обрушениями доли морской поверхности от скорости ветра и возраста ветровых волн a приводит к соответствующим зависимостям s₀ от модуля скорости ветра U и возраста волн.

Экспериментально подтвержден вклад обрушений ветровых волн в УЭПР морской поверхности. Получена линейная зависимость s₀ от покрытой обрушениями доли морской поверхности: s₀ = 1.47q. Представленные ветровые зависимости s₀^up и q, полученные в натурных условиях, почти совпадают. Данный результат экспериментально подтверждает принятую модель s₀(U) ∝ q(U) и существенную роль обрушений ветровых волн в формировании рассеянного морской поверхностью РЛ сигнала при больших углах падения. Показано, что степень развития волнения влияет на уровень УЭПР,
который при одинаковом ветре в направлении «на ветер» увеличивается в пять раз с ростом возраста волн от 0.1 до 1.2.

Построена геофизическая модельная функция, учитывающая скорость ветра и возраст ветровых волн a. Использование результатов, полученных в рамках геофизической модельной функции, позволяет восстановить скорость ветра и его направление по РЛ данным. Рассчитанные по s₀ модули скорости и направления ветра удовлетворительно совпали с показаниями анемометра. Среднеквадратичные ошибки восстановленных значений U_RL и j_w составили 1.2 м/с и 30° соответственно.

1. On radar imaging of current features: 2. Mesoscale eddy and current front detection / J. A. Johannessen [et al.] // Journal of Geophysical Research. 2005. Vol. 110, iss. C7. C07017. https://doi.org/10.1029/2004JC002802

2. On dual co-polarized SAR measurements of the ocean surface / V. N. Kudryavtsev [et al.] // IEEE Geoscience and Remote Sensing Letters. 2013. Vol. 10, iss. 4. P. 761–765. https://doi.org/10.1109/LGRS.2012.2222341

3. A semiempirical model of the normalized radar cross-section of the sea surface. 1. Background model / V. N. Kudryavtsev [et al.] // Journal of Geophysical Research: Oceans. 2003. Vol. 108, iss. C3. 8054. https://doi.org/10.1029/2001JC001003

4. Sample application of a low-cost X-band monitoring system of surface currents at the Black Sea shore / D. V. Ivonin [et al.] // Russian Journal of Earth Sciences. 2011. Vol. 12, iss. 2. P. 1–8. ES2003. https://doi.org/10.2205/2011ES000507

5. Ermoshkin A. V., Kapustin I. A. Estimation of the wind-driven wave spectrum using a high spatial resolution coherent radar // Russian Journal of Earth Sciences. 2019. Vol. 19, iss. 3. ES1005. https://doi.org/10.2205/2019ES000662

6. Определение скорости течения на морской поверхности доплеровским радиоло-катором X-диапазона / А. В. Ермошкин [и др.] // Фундаментальная и прикладная гидрофизика. 2020. Т. 13, № 3. С 93–103. EDN PSBVIF. https://doi.org/10.7868/S2073667320030089

7. Real-time ocean wind vector retrieval from marine radar image sequences acquired at grazing angle / R. Vicen-Bueno [et al.] // Journal of Atmospheric and Oceanic Tech-nology. 2013. Vol. 30, iss. 1. P. 127–139. https://doi.org/10.1175/JTECH-D-12-00027.1

8. Lund B., Graber H. C., Romeiser R. Wind retrieval from shipborne nautical X-band radar data // IEEE Transactions on Geoscience and Remote Sensing. 2012. Vol. 50, iss. 10. P. 3800–3811. https://doi.org/10.1109/TGRS.2012.2186457

9. Dankert H., Horstmann J., Rosenthal W. Ocean wind fields retrieved from radar-image sequences // Journal of Geophysical Research. 2003. Vol. 108, iss. C11. 3352. https://doi.org/10.1029/2003JC002056

10. Малиновский В. В. Оценка связи параметров радиолокационного сигнала, отраженного от моря при малых углах скольжения, с характеристиками обрушений ветровых волн // Морской гидрофизический журнал. 1991. № 6. С. 32–41.

11. Hwang P. A., Sletten M. A., Toporkov J. V. Breaking wave contribution to low grazing angle radar backscatter from the ocean surface // Journal of Geophysical Research: Oceans. 2008. Vol. 113, iss. C9. C09017. https://doi.org/10.1029/2008JC004752

12. Ермошкин А. В., Баханов В. В., Богатов Н. А. Развитие эмпирико-теоретической модели рассеяния радиолокационных сигналов взволнованной водной поверх-ностью при скользящих углах наблюдения // Современные проблемы дистанци-онного зондирования Земли из космоса. 2015. Т. 12, № 4. С. 51–59. EDN UITZQL.

13. Zhao D., Toba Y. Dependence of whitecap coverage on wind and wind-wave properties // Journal of Oceanography. 2001. Vol. 57. P. 603–615. https://doi.org/10.1023/A:1021215904955

14. Whitecap coverage dependence on wind and wave statistics as observed during SO GasEx and HiWinGS / S. E. Brumer [et al.] // Journal of Physical Oceanography. 2017. Vol. 47, iss. 9. P. 2211–2235. https://doi.org/10.1175/JPO-D-17-0005.1

15. Dulov V. A., Skiba E. V., Kubryakov A. A. Landsat-8 observations of foam coverage under fetch-limited wave development // Remote Sensing. 2023. Vol. 15, iss. 9. 2222. https://doi.org/10.3390/rs15092222

16. Bulk parameterization of air-sea fluxes: updates and verification for the COARE algo-rithm / C. W. Fairall [et al.] // Journal of Climate. 2003. Vol. 16, iss. 4. P. 571–591. https://doi.org/10.1175/1520-0442(2003)016<0571:BPOASF>2.0.CO;2

17. Hanson J. L., Phillips O. M. Wind sea growth and dissipation in the open ocean // Journal of Physical Oceanography. 1999. Vol. 29, iss. 8. P. 1633–1648. https://doi.org/10.1175/1520-0485(1999)029<1633:WSGADI>2.0.CO;2

18. Mironov A. S., Dulov V. A. Detection of wave breaking using sea surface video records // Measurement Science and Technology. 2008. Vol. 19, iss. 1. 015405. https://doi.org/10.1088/0957-0233/19/1/015405

19. Статистические характеристики обрушений ветровых волн и их связь с диссипацией энергии по данным натурных измерений / А. Е. Кориненко [и др.] // Морской гидрофизический журнал. 2020. Т. 36, № 5. С. 514–531. EDN RNDETW. https://doi.org/10.22449/0233-7584-2020-5-514-531

20. Малиновский В. В., Кориненко А. Е., Кудрявцев В. Н. Эмпирическая модель ра-диолокационного рассеяния в диапазоне длин волн 3 см на морской поверхности при больших углах падения // Известия высших учебных заведений. Радиофизи-ка. 2018. Т. 61, № 2. С. 110–121. EDN XSAOHB.

21. On radar imaging of current features: 1. Model and comparison with observations / V. N. Kudryavtsev [et al.] // Journal of Geophysical Research. 2005. Vol. 110, iss. C7. https://doi.org/10.1029/2004JC002505

22. Phillips O. M. Radar returns from the sea surface – Bragg scattering and breaking waves // Journal of Physic Oceanography. 1988. Vol. 18, iss. 8. P. 1065–1074. https://doi.org/10.1175/1520-0485(1988)018<1065:RRFTSS>2.0.CO;2

23. Monahan E. C., Woolf D. K. Comments on “Variations of whitecap coverage with wind stress and water temperature” // Journal of Physical Oceanography. 1989. Vol. 19, iss. 5. P. 706–709. https://doi.org/10.1175/1520-0485(1989)019<0706:COOWCW>2.0.CO;2

24. Kleiss J. M., Melville W. K. Observations of wave breaking kinematics in fetch-limited seas // Journal of Physical Oceanography. 2010. Vol. 40, iss. 12. P. 2575–2604. https://doi.org/10.1175/2010JPO4383.1

25. Bortkovskii R. S., Novak V. A. Statistical dependencies of sea state on water tempera-ture and wind-wave age // Journal of Marine Systems. 1993. Vol. 4, iss. 2–3. P. 161–169. https://doi.org/10.1016/0924-7963(93)90006-8

26. Anguelova M. D., Webster F. Whitecap coverage from satellite measurements: A first step toward modeling the variability of oceanic whitecaps // Journal of Geophysical Research: Oceans. 2006. Vol. 111, iss. C3. C03017. https://doi.org/10.1029/2005JC003158

27. Sutherland P., Melville W. K. Field measurements and scaling of ocean surface wave-breaking statistics // Geophysical Research Letters. 2013. Vol. 40, iss. 12. P. 3074–3079. https://doi.org/10.1002/grl.50584

28. Кориненко А. Е., Малиновский В. В., Кудрявцев В. Н. Экспериментальные исследования статистических характеристик обрушений ветровых волн // Морской гидрофизический журнал. 2018. Т. 34, № 6. C. 534–547. EDN YPUYXR. https://doi.org/10.22449/0233-7584-2018-6-534-547

29. Trizna D. B., Carlson D. J. Studies of dual polarized low grazing angle radar sea scatter in nearshore regions // IEEE Transactions on Geoscience and Remote Sensing. 1996. Vol. 34, iss. 3. P. 747–757. https://doi.org/https://doi.org/10.1109/36.499754

30. Azimuthal dependence of the radar cross section and the spectral background noise of a nautical radar at grazing incidence / H. Hatten [et al.] // Proceedings of IGARSS. Sensing and Managing the Environment. IEEE International Geoscience and Remote Sensing Symposium. Seattle, WA. USA. 6–10 July. IEEE Publications, 1998. Vol. 5. P. 2490–2492. https://doi.org/10.1109/IGARSS.1998.702255

31. Normalized radar cross section of the sea for backscatter: 1. Mean levels / W. Plant [et al.] // Journal of Geophysical Research: Oceans. 2010. Vol. 115, iss. C9. C09032. https://doi.org/10.1029/2009JC006078

32. Wentz F. J., Peteherych S., Thomas L. A. A model function for ocean radar cross sec-tion at 14.6 GHz // Journal of Geophysical Research: Oceans. 1984. Vol. 89, iss. C3. P. 3689–3704. https://doi.org/10.1029/JC089iC03p03689