УДК 539.3 Механика деформируемых тел. Упругость. Деформации
УДК 534.12 Колебания двумерных тел (поверхностей)
Цель. Цель работы – исследование зависимости скорости движения однородной жидкости в направлении распространения волны, сформированной при нелинейном взаимодействии волновых гармоник, от характеристик ледового покрова. Методы и результаты. На основе потенциала скорости движения жидкости конечной глубины, полученного в виде асимптотического разложения до величин третьего порядка малости, проанализирована скорость движения частиц жидкости под плавающим упругим льдом при нелинейном взаимодействии волновых гармоник. Изучено влияние толщины и модуля упругости ледового покрова, нелинейности вертикального ускорения льда, амплитуды второй взаимодействующей гармоники на составляющие орбитальной скорости движения жидких частиц под плавающим льдом. Выводы. Показано, что влияние нелинейности ускорения вертикальных смещений плавающего льда на составляющие скорости движения жидкости проявляется в увеличении фазового сдвига. Смена знака второй взаимодействующей гармоники приводит к преобразованию профилей и к уменьшению фазы. Увеличение значения модуля Юнга проявляется в заметном увеличении фазового сдвига и слабом росте максимальных значений составляющих скорости движения жидкости в сравнении со случаем, когда лед отсутствует.
нелинейное взаимодействие волн, изгибно-гравитационные волны, волны конечной амплитуды, движение частиц жидкости
Введение
Скорости поступательного перемещения жидкости в направлении дви-жения волн конечной амплитуды изучались в работах [1–3] при бесконечной, а в [4–6] при конечной глубине бассейна со свободной поверхностью. В ли-нейной постановке влияние плавающего битого льда на скорость волновых течений в однородной жидкости исследовано в статье [7]. Зависимость со-ставляющих орбитальной скорости движения частиц жидкости с открытой поверхностью от характеристик бегущей периодической волны конечной ам-плитуды изучена в [8], а под плавающим упругим ледовым покровом – в ра-боте [9]. Экспериментальные исследования влияния скорости подледных те-чений на параметры изгибно-гравитационных волн представлены в [10].
В настоящей работе на основе полученного решения задачи о колебани-ях, формируемых при нелинейном взаимодействии гармоник прогрессивных поверхностных волн в системе лед – жидкость [11], проанализирована зави-симость распределения составляющих орбитальной скорости движения ча-стиц однородной жидкости по длине сформированной волны от характери-стик ледового покрова. Полученные результаты могут быть использованы для интерпретации результатов лабораторных и натурных наблюдений, при разработке технологий и систем мониторинга морских бассейнов в ледовый период.
Постановка задачи
Рассмотрим однородную идеальную несжимаемую жидкость постоянной глубины H, ее поверхность покрыта плавающим льдом с толщиной h = const. Жидкость и ледовый покров в горизонтальных направлениях не ограничены. Изучим влияние льда на орбитальные скорости движения жидких частиц, формируемые при взаимодействии двух гармоник волн конечной амплитуды. Предположим движение жидкости потенциальным, колебания льда безотрывными, безразмерные переменные x = kx1, z = kz1, t = kg t1 , ζ = kζ∗ , φ = (k 2 kg )φ∗ , где k – волновое число; g – ускорение силы тяжести; t – вре-
мя; φ(x, z, t) – потенциал скорости движения жидкости, тогда задача заключается в решении уравнения Лапласа
для потенциала скорости с граничными условиями на поверхности лед жидкость (z = ζ)
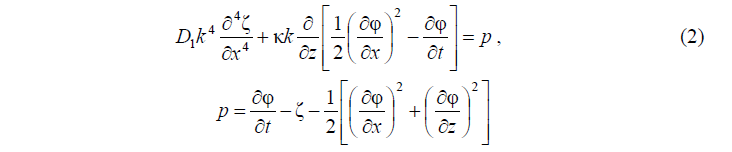
и на дне (z = –H) бассейна
В начальный момент времени (t = 0)
Здесь
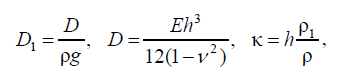
Е, h, ρ1, ν – модуль нормальной упругости, толщина, плотность, коэффициент Пуассона льда соответственно; ρ – плотность жидкости; ζ(x, t) – возвышение поверхности лед – жидкость, в начальный момент времени равное функции f(x). Потенциал скорости и возвышение поверхности лед – жидкость при z = ζ
связаны кинематическим условием
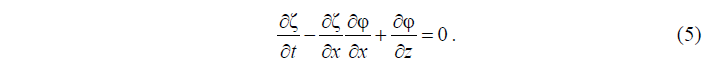
В динамическом условии (2) выражение со множителем κ представляет собой инерцию вертикальных смещений льда, где первое слагаемое в скобках этого выражения характеризует нелинейность его вертикального ускорения [11].
Выражения для составляющих орбитальной скорости движения частиц
жидкости
Решение задачи (1) – (5) было найдено методом многих масштабов [12] в виде уравнений для трех приближений, учитывающих нелинейность ускорения вертикальных смещений упругого льда [11]. Рассмотрим периодические волны, задавая функцию f(x) в соответствующем виде. Для случая взаимодействия бегущих периодических волн, когда первое приближение задано в виде
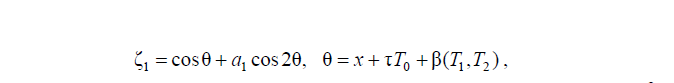
где a1 – амплитуда второй взаимодействующей гармоники; tTtT221ε,ε==, а β(Т1, Т2) определяется из второго и третьего приближений, выражение, определяющее потенциал скорости с точностью до третьего приближения в безразмерных переменных, имеет вид
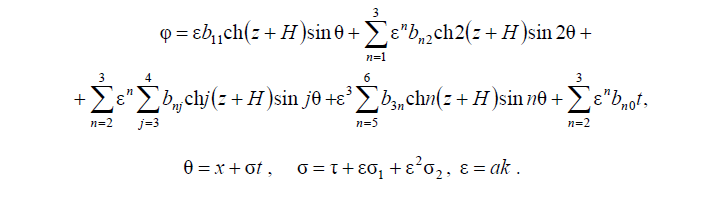
Здесь
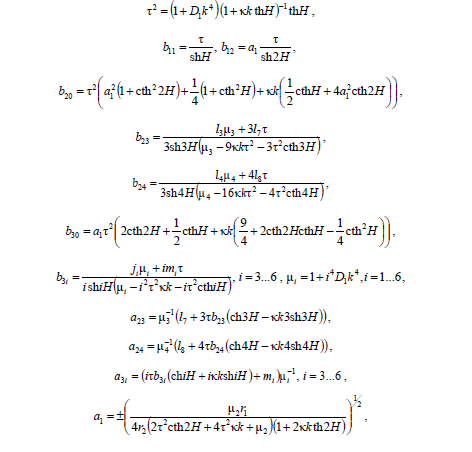
При этом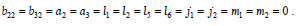 
. В размерных переменных выражение для потенциала скорости имеет следующий вид:
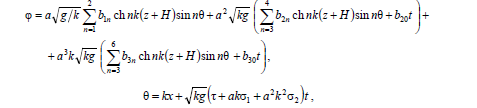
а в выражениях для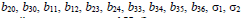 
аргумент гиперболических функций заменяется на kH. Здесь и далее для выражений в размерных переменных у символов «x», «z», «t» опущен индекс 1, а у «ϕ» – знак «*».
Таким образом, горизонтальная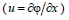 
и вертикальная 
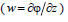составляющие скорости движения однородной жидкости определяются вы-ражениями
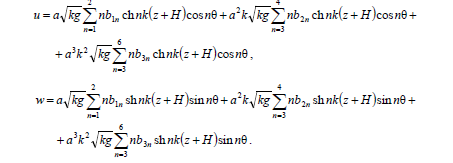
Отметим, что полученное решение справедливо вне малых окрестностей резонансных значений волновых чисел ki (i = 1 … 4), являющихся положи-тельными действительными корнями уравнений [11]
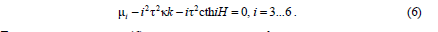
Левая часть выражения (6) входит в знаменатель b3i.
Анализ влияния ледового покрова на составляющие скорости
движения жидкости
Оценка влияния характеристик плавающего льда на составляющие ско-рости в направлении движения нелинейной волны выполнялась при 1ρ/ρ0,87,0,34,02мhν==≤≤ и E, равном 0, 5·108; 109; 3·109 Н/м2.
Распределения u и w вдоль профиля волны представлены на рис. 1 при t = 3 ч, a = 1 м, λ = 392,5 м, Н = 45 м, h = 1 м, E = 3·109 Н/м2 с учетом и без учета вертикального ускорения льда. Видно, что при распространении сфор-мированной нелинейной волны в отрицательном направлении оси Х влияние учета нелинейности ускорения вертикальных смещений льда на составляющие скорости движения жидкости проявляется в увеличении фазового сдвига. Смена знака второй взаимодействующей гармоники с плюса на минус приводит к заметному преобразованию профилей и к уменьшению фазы (рис. 1, b). Профили u и w, полученные с учетом нелинейности вертикального ускорения, отстают от профилей, полученных без ее учета. Форма образованного возмущения является нелинейной.
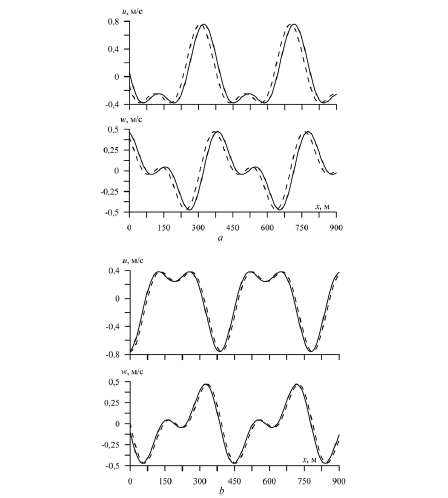
Р и с. 1. Распределение составляющих скорости движения жидкости вдоль профиля нелинейной волны при а1 > 0 (а) и а1 < 0 (b) при λ/H = 8,72 c учетом (штриховая линия) и без учета (сплошная линия) вертикального ускорения льда
F i g. 1. Distribution of the components of the fluid movement velocity along the profile of a nonlinear wave at а1 > 0 (а) and а1 < 0 (b) at λ/H = 8.72 with the regard (dashed line) and with no regard (solid line) for the ice vertical acceleration
В случае коротких волн (рис. 2) влияние нелинейности вертикального ускорения сохраняет свою направленность, а форма профиля в диапазоне рассмотренных волновых чисел остается нелинейной. На рис. 2 представлено распределение составляющих скорости при t = 540 с, a = 0,6 м, λ = 62,8 м, Н = 70 м, h = 0,6 м, E = 3·109 Н/м2. Для экстремальных значений на профиле горизонтальной составляющей скорости так же, как в линейном случае и в случае распространения периодической волны конечной амплитуды [9], значения вертикальной составляющей равны нулю. В то же время экстре-мальным значениям на профиле вертикальной составляющей скорости соот-ветствуют ненулевые значения ее горизонтальной составляющей.
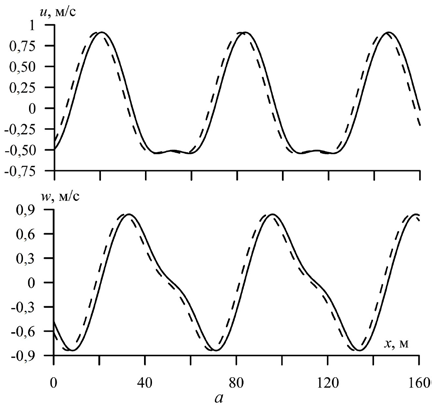
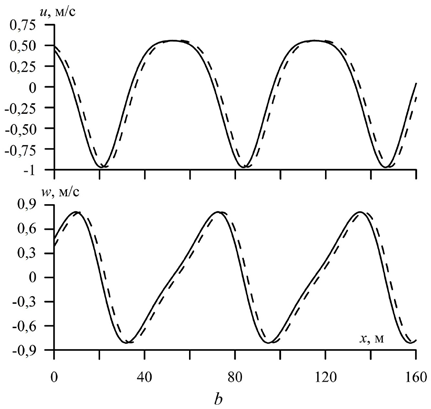
Р и с. 2. Распределение составляющих скорости движения жидкости вдоль профиля нелиней-ной волны при а1 > 0 (а) и а1 < 0 (b) при λ/H = 0,89 – c учетом (штриховая линия) и без учета (сплошная линия) вертикального ускорения льда
F i g. 2. Distribution of the components of the fluid movement velocity along the profile of a nonlin-ear wave at а1 > 0 (а) and а1 < 0 (b) at λ/H = 0.89 with the regard (dashed line) and with no regard (solid line) for the ice vertical acceleration
Влияние модуля упругости сплошного ледового покрова на составляю-щие скорости в случае учета вертикального ускорения льда представлено на рис. 3. Здесь t = 9900 с, a = 2 м, λ = 785 м, Н = 70 м, h = 2 м. Из рисунка видно, что увеличение жесткости льда проявляется в заметном увеличении фазового сдвига и незначительном росте максимальных значений составляющих ско-рости движения жидкости. Смена знака a1 с плюса на минус деформирует профиль качественно и количественно (рис. 3, b). При этом увеличение жест-кости льда, как и при a1 > 0, ведет к заметному увеличению фазы относитель-но фазового сдвига, когда E = 0.
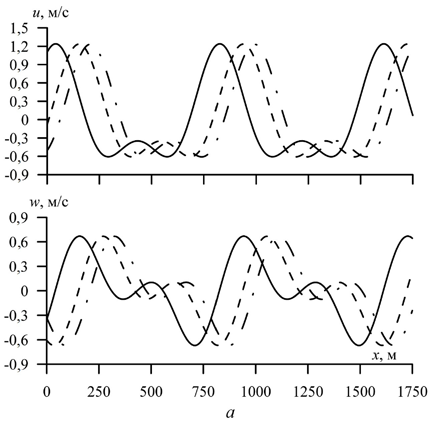
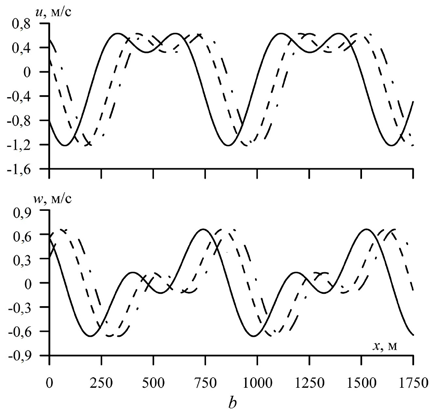
Р и с. 3. Распределение составляющих скорости движения жидкости вдоль профиля нелиней-ной волны с учетом вертикального ускорения льда при а1 > 0 (а) и а1 < 0 (b). Сплошная линия соответствует значению Е = 3·109 Н/м2, штриховая – Е = 109 Н/м2, штрихпунктирная – Е = 0
F i g. 3. Distribution of the components of the fluid movement velocity along the profile of a nonlin-ear wave with the regard for the ice vertical acceleration at а1 > 0 (а) and а1 < 0 (b). Solid line corre-sponds to value Е = 3·109 N/m2, dashed line – to Е = 109 N/m2 and dashed-dotted one – to Е = 0
Отношение максимальных величин вертикальной составляющей скоро-сти (W) и горизонтальной составляющей скорости (U) для случая битого льда (h ≠ 0, E = 0) при учете нелинейности вертикального ускорения и для случая, когда лед отсутствует (h = 0), представлено на рис. 4. Здесь a = 1 м, H = 30 м, E = 0. Сплошная линия – h = 1 м, a1 > 0; штриховая – h = 1 м, a1 < 0; штрихпунктирная с двумя точками – h = 0, a1 > 0; штрихпунктирная – линей-ное приближение при h = 1 м, a1 > 0. Из анализа графиков следует, что в рас-сматриваемом диапазоне волновых чисел распределение значений W/U по k меньше единицы, следовательно, при распространении сформированной нелинейной волны вертикальная составляющая скорости не превосходит го-ризонтальную. Это наблюдается и при распространении периодической вол-ны конечной амплитуды [9]. В области малых значений волновых чисел из-менение W/U происходит не монотонно, исключая линейное приближение. С ростом k при наличии льда уменьшаются значения отношения составляю-щих скорости по сравнению со случаем отсутствия ледового покрова на по-верхности жидкости. При этом для линейного приближения значения отно-шения W/U, полученные при a1 > 0 и h ≠ 0, наименьшие.
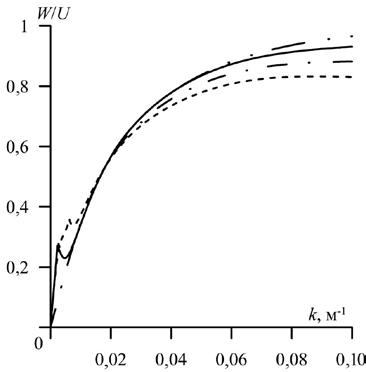
Р и с. 4. Распределение величины отношения W/U по волновому числу при E = 0
F i g. 4. Distribution of the ratio W/U value over the wave number at E = 0
Влияние амплитуды второй взаимодействующей гармоники на отноше-ние W/U при учете нелинейности вертикального ускорения льда и E ≠ 0 пока-зано на рис. 5 для длинноволнового диапазона волновых чисел, где отсут-ствуют резонансные значения [11]. Здесь E = 3·109 Н/м2, H = 100 м, a = 1 м, h = 1 м. Сплошная и штриховая линии соответствуют случаям a1 > 0 и a1 < 0 соответственно. Видно, что смена знака а1 проявляется как в увеличении зна-чений отношения W/U, так и в их уменьшении. С ростом k разница между значениями растет. Отметим, что в коротковолновом диапазоне величина от-ношения W/U при E ≠ 0 и a1 > 0 больше величины отношения W/U при E = 0 и a1 > 0, а при E ≠ 0 и a1 < 0 меньше, чем при E = 0 и a1 < 0.
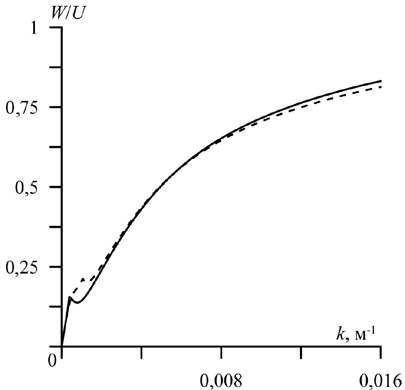
Р и с. 5. Распределение величины отношения W/U по волновому числу при E = 3·109 Н/м2
F i g. 5. Distribution of the ratio W/U value over the wave number at E = 3·109 N/m2
Заключение
На основе потенциала скорости движения жидкости конечной глубины, полученного в виде асимптотического разложения до величин третьего по-рядка малости, проанализирована скорость движения частиц жидкости под плавающим упругим льдом при нелинейном взаимодействии волновых гар-моник. Изучено влияние толщины и модуля упругости ледового покрова, не-линейности вертикального ускорения льда, амплитуды второй взаимодей-ствующей гармоники на составляющие орбитальной скорости движения жидких частиц под плавающим льдом. Исследовано влияние плавающего битого льда на составляющие скорости, а также рассмотрен случай распро-странения сформированной волны конечной амплитуды в бассейне со сво-бодной поверхностью.
Показано, что влияние нелинейности ускорения вертикальных смещений плавающего льда на составляющие скорости движения жидкости проявляется в увеличении фазового сдвига. Смена знака второй взаимодействующей гар-моники приводит к существенному преобразованию профилей и уменьше-нию фазы. Это влияние проявляется в случае как коротких, так и длинных волн. Таким образом, пренебрежение нелинейностью вертикального ускоре-ния льда может привести к заметным погрешностям в определении фазового сдвига.
Увеличение значения модуля Юнга приводит к увеличению фазового сдвига и незначительному росту максимальных величин составляющих ско-рости движения жидкости с плавающим льдом в сравнении со случаем, когда лед отсутствует. Растет фаза и при увеличении толщины упругого льда, а в случае битого льда она уменьшается.
Отношение максимальных величин вертикальной и горизонтальной со-ставляющих скорости в рассматриваемом диапазоне волновых чисел при мо-дуле упругости, равном нулю, меньше единицы. Следовательно, при распространении волны, сформированной при нелинейном взаимодействии волно-
вых гармоник, вертикальная составляющая скорости не превосходит горизонтальную. Это наблюдается и при распространении периодической волны конечной амплитуды. Сравнение распределений отношения W/U, полученных с учетом и без учета нелинейности вертикального ускорения упругого льда, говорит о ее слабом влиянии на отношение. При этом смена знака амплитуды второй взаимодействующей гармоники как при отсутствии, так и при наличии упругости льда имеет заметное влияние.
1. Нестеров С. В. Возбуждение волн конечной амплитуды бегущей системой давлений // Известия АН СССР. Физика атмосферы и океана. 1968. Т. 4, № 10. С. 1123–1125.
2. Ньюмен Д. Морская гидродинамика. Л. : Судостроение, 1985. 367 с.
3. Longuet-Higgins M. Lagrangian moments and mass transport in Stokes waves // Journal of Fluid Mechanics. 1987. Vol. 179. P. 547–555. https://doi.org/10.1017/S0022112087001654
4. Сретенский Л. Н. Теория волновых движений жидкости. М. : Наука, 1977. 815 с.
5. Алешков Ю. З. Течения и волны в океане. СПб. : Изд-во С.-Петербургского университета, 1996. 224 с.
6. Longuet-Higgins M. S. Lagrangian moments and mass transport in Stokes waves. Part 2. Water of finite depth // Journal of Fluid Mechanics. 1988. Vol. 186. P. 321–336. https://doi.org/10.1017/S0022112088000163
7. Букатов А. Е., Жарков В. В. Влияние битого льда на скорость волновых течений при прохождении прогрессивных волн над уступом дна // Морской гидрофизический журнал. 2001. № 5. С. 3–14.
8. Букатов Ант. А., Букатова О. М. Скорости движения жидкости в бегущей периодической волне конечной амплитуды // Системы контроля окружающей среды. Севастополь : МГИ НАН Украины, 2008. Вып. 11. С. 269–271.
9. Букатов Ант. А., Букатов Анд. А. Скорости движения жидких частиц под плавающим ледяным покровом при распространении периодической волны конечной амплитуды // Морской гидрофизический журнал. 2011. № 1. С. 15–24.
10. Влияние подледного течения на параметры изгибно-гравитационных волн, возникающих от движения подводного судна под ледяным покровом / В. Л. Земляк [и др.] // Вестник Приамурского государственного университета им. Шолом-Алейхема. 2014. № 4 (17). С. 40–47.
11. Букатов А. Е., Букатов А. А. Колебания плавающей упругой пластины при нелинейном взаимодействии изгибно-гравитационных волн // Прикладная механика и техническая физика. 2018. Т. 59, № 4. С. 99–109. doihttps://doi.org/10.15372/PMTF20180412
12. Найфэ А. Х. Методы возмущений. М. : Мир, 1976. 455 с.
