Россия
Россия
Цель. Цель исследования – выявить временные интервалы с 50-х гг. XX в., когда среднегодовые высоты волн в Балтийском море имели тенденции к росту или снижению, оценить стати-стическую значимость потенциальных временных трендов, а также определить характер статистической связи среднегодовых высот волн на Балтике с североатлантическим колебанием. Методы и результаты. Для анализа было выбрано несколько точек, расположенных в различных частях Балтийского моря, данные о среднегодовых высотах волн в которых охватывали временные интервалы длительностью несколько десятков лет и были получены инструментальными методами (одна точка), по натурным наблюдениям (две точки) и по результатам моделирования (шесть точек). Временные серии среднегодовых высот волн в этих точках были разделены на временные отрезки условной монотонности с преимущественными тенденциями к росту или снижению. Оценка скоростей изменения высоты волн на каждом из отрезков и статистической значимости потенциальных временных трендов проводилась непараметрическими методами. Оказалось, что в большинстве случаев тренды на рассматриваемых временных отрезках статистически значимы на уровне 90% и более, а скорости изменения по тренду могут составлять от 5 до 20 мм/год. Статистическая связь среднегодовых высот волн с северо-атлантическим колебанием оценивалась с помощью корреляционного анализа Пирсона и Спирмена. Коэффициенты корреляции между индексами североатлантического колебания и среднегодовыми высотами волн оказались статистически значимыми на уровне 90% и более. Их численные значения в рамках межгодовой изменчивости составили 0,3–0,6, между скользящими пятилетними средними 0,4–0,8. Выводы. Фазы роста и снижения высот волн в Балтийском море чередуются, а продолжительность каждой из фаз составляет 20 лет. Временные тренды для каждой из фаз статистически значимы, по крайней мере в некоторых точках моря. Корреляционная связь между индексом североатлантического колебания и среднегодовыми высотами волн статистически значима, но не высока. Такая корреляция может объяснить 30–65% изменения волновых характеристик.
Балтийское море, значительная высота волны, NAO индекс, временной тренд, статистическая значимость, коэффициент корреляции
Введение
Можно считать, что визуальные наблюдения ветроволновой обстановки на Балтике с ее письменной фиксацией проводятся на судах и в различных частях побережья с начала XIX в. [1], т. е. с того времени, когда появилась известная шкала Бофорта для оценки силы ветра и высоты волнения, признанная впоследствии Всемирной метеорологической организацией При визуальных наблюдениях человек интуитивно концентрирует свое внимание на относительно больших волнах, не обращая внимание на мелкие, т. е. оценивает не высоту индивидуальных волн, а некое общее состояние моря [2, c. 49–50]). Очевидно, что такие оценки достаточно субъективны и не очень точны. Инструментальные измерения с точной фиксацией параметров волнения начались в Балтийском море лишь в 70-х гг. прошлого века [3]. Современные волнографы позволяют определить как характеристики индивидуальных волн, проходящих через точку установки прибора, так и статистические параметры волнения, которые можно соотнести со шкалой Бофорта.
Одной из самых важных статистических характеристик волнения является так называемая «значительная» высота волны (significant wave height, SWH), определяемая как средняя высота одной трети самых высоких волн из зарегистрированных в данной точке. Именно этот параметр опытный наблюдатель зрительно оценивает как «высоту» волны. Далее в работе будет идти речь именно о «значительных» высотах волн и мы будем использовать аббревиатуру SWH.
Исследованию параметров волнового режима Балтийского моря посвящено много работ [4]. Однако основное внимание авторы большинства из них уделяют пространственному распределению SWH. Временная изменчивость анализируется в гораздо меньшем количестве работ [1, 5–9].
Параметры волнового режима Балтийского моря непосредственно связаны с глобальными процессами циркуляции атмосферы, в частности с циклонической активностью. Известно [10, с. 11–12], что на траектории и интенсивность атмосферных вихрей над Атлантикой и Европой в значительной степени влияет так называемое североатлантическое колебание (North Atlantic Circulation, NAO). Типичное состояние атмосферы над Северной Атлантикой характеризуется Азорским максимумом и Исландским минимумом. Если эти экстремумы ярко выражены (между ними существует большой перепад давления), мы имеем дело с положительной фазой NAO, в противном случае – с отрицательной. Для количественной оценки явления используется индекс NAO, среднемесячные значения которого с января 1950 г. по настоящее время публикуются Центром прогноза климата США
Работы, посвященные анализу связи североатлантического колебания с высотами волн в различных акваториях, появились в 90-х гг. прошлого века. Так, в работе [11] рассматривается зависимость в период 1962–1988 гг. между SWH в Северной Атлантике и градиентом давления между Азорским максимумом и Исландским минимумом. Отмечается наличие статистической связи как между среднегодовыми, так и между среднемесячными значениями сравниваемых величин. Здесь же впервые делается предположение, что с североатлантическим колебанием прежде всего связана межгодовая изменчивость SWH, а не многолетние тренды. Это предположение для региона Северной Атлантики и Северного моря далее развивается в работах [12–14], причем отмечается, что среднегодовые SWH лучше коррелируют с индексами NAO, усредненными за зимние месяцы (с декабря по март), чем среднемесячные SWH и среднемесячные индексы NAO между собой.
Остановимся кратко на работах, посвященных исследованию связи североатлантического колебания и высот волн в Балтийском море. В работе [7] на основе данных моделирования за 44 года (1958–2001) указывается, что связь имеет место, но никаких численных значений не приводится. В работе [5] отмечается корреляция с коэффициентом 0,61 между среднегодовыми SWH у эстонского побережья за период 1966–2006 гг. и индексами NAO, усредненными за период август – февраль. В то же время в работе [15], где рассматривается связь среднегодовых SWH у побережья Польши за период 1958–2002 гг. со среднегодовыми индексами NAO, а также среднемесячных SWH со среднемесячными индексами NAO, автор приходит к выводу, что связь хотя и существует, но является достаточно слабой.
В работах [16, 17] рассматривались только штормовые события. Связь среднегодовых или среднемесячных SWH с индексами NAO не анализировалась. Было выявлено существование корреляционной связи на уровне 30–50% между количеством штормовых событий на Балтике (с SWH > 2 м) и индексом NAO.
В работе [18] анализируются результаты моделирования волновой обстановки у южного побережья Швеции за 62 года (1959–2021). Отмечается, что межгодовая изменчивость среднегодовых энергий и направлений распространения волн находится в существенной корреляционной связи с зимними индексами NAO (усредненными за декабрь – март). Количественно статистическая связь измеряется коэффициентом корреляции Спирмена, который для различных точек в прибрежной зоне составляет 0,5–0,7.
Как видно по краткому обзору опубликованных работ, существование корреляционной связи параметров волнового режима на Балтике и NAO не вызывает сомнений, однако ряд вопросов остается открытым. К таким вопросам прежде всего можно отнести следующие: какой из вариантов усреднения индексов NAO показывает наилучшую корреляцию с параметрами волнения и какова степень влияния NAO на параметры волнения в рамках межгодовой и многолетней изменчивости.
В предыдущих работах авторов [8, 9] рассматривались параметры волнового режима Балтийского моря по результатам численного моделирования за период 1979–2018 гг., были выявлены временные тенденции изменения SWH в тех или иных областях и оценена статистическая значимость этих тенденций. Цель настоящего исследования – охватить период с 50-х гг. XX в. по 20-е гг. XXI в., выявить временные интервалы, когда среднегодовые SWH на Балтике имели тенденции к росту или снижению, оценить их статистическую значимость, а также попытаться определить характер статистической связи среднегодовых SWH с индексом NAO.
Материалы и методы
Данные, использованные для анализа. Рассмотрим динамику высот волн в Балтийском море. Расположение точек и временные серии среднегодовых SWH, использованные для анализа, показаны на рис. 1. Градации серого отражают информацию о пространственном распределении средних SWH (за период 1979–2018 гг.). Данные о временных сериях среднегодовых SWH в точках 1, 2 и 3 взяты из литературных источников [1, 5, 6], в точках 4–9 – являются результатами, полученными авторами. Рассмотрим более подробно методику получения данных для каждой из представленных на рис. 1 точек.

Р и с. 1. Многолетняя динамика высот волн в Балтийском море. Цветом и изолиниями показаны средние SWH в Балтийском море по данным численного моделирования за период 1979–2018 гг. [8, 9]. Белыми цифрами выделены точки, использованные для исследования. На врезках – временные серии среднегодовых SWH для каждой из точек и линейные аппроксимации для участков, которые можно считать условно монотонными при зрительном анализе
F i g. 1. Long-term dynamics of wave heights in the Baltic Sea. Color and isolines show the average SWH in the Baltic Sea based on numerical simulating data for 1979–2018 [8, 9]. White numerals highlight the points used in the study. Insets show the time series of annual average SWH for each point and the linear approximations for the areas that can be considered supposedly monotonic in visual analysis
Высоты волн у побережья Латвии в районе Лиепаи (точка 1 на рис. 1) оценивались по результатам визуальных наблюдений. В работе [6] представлены данные о среднегодовых SWH, полученных таким методом за период 1949–1984 гг. Эти материалы легли в основу построения временной серии на врезке для точки 1. Для эстонских берегов (точка 2) использовались результаты, представленные в работе [5]. Автор исследования проводил расчеты по полуэмпирической модели, основанной на зависимости высоты волн от длины их разгона. Для учета ветрового воздействия использовались данные метеостанции Vilsandi, расположенной вблизи западной оконечности о. Сааремаа. Расчеты среднегодовых SWH в этом районе были выполнены для периода 1966–2006 гг. Точка 3 отражает результаты пионерских инструментальных измерений SWH на Балтике, выполненных волновым регистратором Almagrundet, установленным в нескольких десятках километров от побережья Швеции. Результаты, описанные в работе [1], охватывают период 1979–1995 гг., они легли в основу построения временной серии для точки 3.
Временные серии для точек 4–9 получены авторами с помощью спектральной волновой модели MIKE 21 SW за 40-летний период 1979–2018 гг. Неструктурированная расчетная сетка охватывала все Балтийское море. Размер стороны треугольных элементов сетки изменялся от 2–3 до 10–15 км. Открытых границ модель не имела. Шаг по времени при выполнении расчетов регулировался моделью исходя из выполнения условия устойчивости, но не превышал 10 мин. Для учета ветрового воздействия использовались открытые данные реанализа ERA-Interim на пространственной сетке в 1° по широте и долготе с временным шагом 6 ч. Калибровка и верификация модели проводились путем сравнения результатов расчетов с данными волновых буев, расположенных в различных частях Балтийского моря. Подробные сведения о настройках, калибровке и верификации модели, использованной для расчетов, приведены в [8, 9]. Выбор местоположения точек 4–9 из всего массива данных был обусловлен тем, что по модельным расчетам за период 1979–2018 гг. в них были получены максимальные значительные высоты волн для разных субрегионов Балтийского моря.
Анализ временной изменчивости среднегодовых высот волн. Анализ динамики среднегодовых SWH проводился путем исследования их временных серий в перечисленных выше точках Балтийского моря. Каждая из рассматриваемых временных серий подвергалась обработке, включающей три этапа.
На первом этапе зрительно выявлялись временные интервалы, когда зависимость среднегодовых SWH от времени условно можно было считать линейной. Аппроксимирующие их линейные функции показаны в виде отрезков прямых линий на врезках. Далее для каждого из выявленных интервалов с использованием непараметрического подхода определялся угловой коэффициент линейной аппроксимирующей функции (Sen's slope [19]) и оценивалась статистическая значимость потенциального временного тренда по критерию Манна – Кендалла [20, 21]. Статистический анализ выполнялся в Excel с помощью надстройки Real Statistics для уровня статистической значимости a = 0,1 (90% вероятности). На последнем этапе статистические показатели для разных пространственных точек сравнивались и делались выводы о динамике среднегодовых SWH на том или ином временном интервале.
Оценка связи среднегодовых SWH с индексом NAO. Анализировалась корреляция временных серий среднегодовых SWH с временными сериями индекса NAO для всех точек, показанных на рис. 1. Значения индекса NAO, использованные в данной работе, представляют собой нормализованную разность давлений между метеостанциями Гибралтар и Рейкьявик (Исландия), они рассчитываются по методике из работы [22], а их среднемесячные значения доступны в открытой базе данных Центра прогноза климата США, опубликованной в Интернете . Эти среднемесячные значения и являлись исходными данными для анализа связи NAO с высотой волны на Балтике.
В настоящем исследовании рассматривались как среднегодовые значения индекса NAO, так и его значения, усредненные для различных сочетаний месяцев с октября по март. Особое внимание холодным месяцам уделялось в связи с тем, что зимние процессы взаимодействия океана и атмосферы оказывают наибольшее влияние на циркуляцию атмосферы в последующие месяцы календарного года [23, 24; 10, c. 23]. Например, наиболее часто встречается усреднение индекса NAO для зимних месяцев, имеющее аббревиатуру JFM (январь, февраль, март), которое хорошо коррелирует с различными метеорологическими параметрами [25, 26]. В работах встречаются различные варианты усреднения за период октябрь – март [27, 28].
Оценка связи осуществлялась путем расчета коэффициентов корреляции (КК) Пирсона и Спирмена . Кроме того, была выполнена оценка статистической значимости рассчитанных коэффициентов корреляции для уровня a = 0,1. Статистический анализ выполнялся в Excel с помощью надстройки Real Statistics 5.
Результаты и обсуждение
Анализ временной изменчивости среднегодовых SWH. Зрительный анализ (врезки на рис. 1) показывает, что участки снижения и роста среднегодовых SWH в Балтийском море чередуются. С 1950 г. до конца 60-х – начала 70-х гг. прошлого века наблюдается тенденция к снижению. Скорости снижения составляют от 5 (точка 2) до 23 (точка 1) мм/год. Данных, относящихся к этому периоду, очень мало, и получены они в основном методом визуальных наблюдений. Поэтому результаты достаточно субъективны и не очень надежны.
С конца 60-х – начала 70-х гг. наблюдается тенденция к росту среднегодовых SWH, что подтверждается временными сериями во всех точках. Темпы роста составляют от 6 (точка 9) до 17 (точка 3) мм/год. Здесь данных уже существенно больше. Они получены как визуальными, так и более объективными методами – с помощью инструментальных измерений и математического моделирования.
С начала 90-х гг. прошлого века и примерно до 2010 г. снова проявляется тенденция к снижению среднегодовых SWH. Такой вывод основывается как на результатах расчетов авторов (точки 4–9), так и на результатах моделирования из работы [5] для точки 2. Скорости снижения изменяются от 4 мм/год для точки 8 до 13 мм/год для точки 5. Предположительно с 2010 г. снова начинается фаза роста, однако, поскольку охватываемый данными период ограничивается 2018 г., делать выводы о темпах роста некорректно: период слишком короткий для анализа.
Т а б л и ц а 1
T a b l e 1
Скорость изменения среднегодовых SWH для тех периодов,
когда временные тренды можно считать статистически значимыми
на уровне a = 0,1 (90% вероятности)
Rate of the annual average SWH change for the periods when the time trends can be considered statistically significant at level a = 0.1 (90% probability)
|
Точка / Point |
Период / Period |
Тренд значим при a = 0,1 / Trend is significant at a = 0.1 |
Значение тренда, мм/год / Trend value, mm/year |
|
1 |
1949–1968 |
да / yes |
–23,0 |
|
1968–1985 |
да / yes |
15,0 |
|
|
2 |
1966–1976 |
нет / no |
– |
|
1976–1990 |
да / yes |
7,5 |
|
|
1990–2006 |
да / yes |
–6,0 |
|
|
3 |
1979–1995 |
да / yes |
17,0 |
|
4 |
1979–1992 |
нет / no |
– |
|
1992–2010 |
да / yes |
–8,6 |
|
|
2010–2018 |
нет / no |
– |
|
|
5 |
1979–1992 |
да / yes |
6,9 |
|
1992–2010 |
да / yes |
–13,0 |
|
|
2010–2018 |
нет / no |
– |
|
|
6 |
1979–1993 |
да / yes |
8,8 |
|
1993–2010 |
да / yes |
–9,5 |
|
|
2010–2018 |
нет / no |
– |
|
|
7 |
1979–1993 |
да / yes |
9,0 |
|
1993–2010 |
да / yes |
–8,3 |
|
|
2010–2018 |
нет / no |
– |
|
|
8 |
1979–1993 |
нет / no |
– |
|
1993–2010 |
да / yes |
–4,2 |
|
|
2010–2018 |
нет / no |
– |
|
|
9 |
1979–1993 |
да / yes |
5,9 |
|
1993–2010 |
да / yes |
–7,6 |
|
|
2010–2018 |
нет / no |
– |
Подводя итог, можно предположить, что фазы роста и снижения среднегодовых SWH на Балтике имеют продолжительность ~ 20 лет: с 1950 по 1970 г. – снижение, с 1970 по 1990 г. – рост, с 1990 по 2010 г. – снижение. Темпы изменения среднегодовых SWH пространственно разнятся и могут составлять ~ 5–20 мм/год.
Кроме расчетов темпов изменения среднегодовых SWH были выполнены оценки статистической значимости временных трендов для каждого из рассматриваемых временных интервалов. Расчеты выполнялись для уровня a = 0,1. Статистическая значимость потенциального временного тренда оценивалась непараметрическим методом Манна – Кендалла [20, 21], а значение тренда – по формуле Сена (Sen's slope) [19]. Результаты расчетов представлены в табл. 1.
Период до середины 70-х гг. показан в табл. 1 лишь точками 1 (побережье Балтики у Лиепаи, визуальные наблюдения) и 2 (западная оконечность о. Сааремаа; модель, основанная на длине разгона волн). Видно, что для периода снижения SWH с 1950 г. до начала – середины 70-х гг. тренд в точке 1 статистически значим, в точке 2 – нет. Отсутствие статистической значимости в точке 2 объясняется, прежде всего, очень коротким временным отрезком, охватываемым данными (10 лет потенциального снижения в период 1966–1976 гг.). Для периода роста с 70-х по 90-е гг. имеются данные во всех рассматриваемых точках. Почти везде тренд статистически значим. Исключения составляют точки 4 (Ботническое море) и 8 (Борнхольмский бассейн). С начала 90-х гг. снова наблюдается тенденция к снижению SWH, которая статистически значима во всех точках, охватываемых данными (все точки, кроме 1 и 3). Для периода после 2010 г. наблюдается слабая тенденция к росту SWH и тренды статистически не значимы в связи с коротким временным интервалом, охватываемым данными (8 лет до 2018 г.).
Оценка связи среднегодовых SWH с индексом NAO. Для оценки связи выполнялись расчеты коэффициентов корреляции между временными сериями среднегодовых SWH и индексов NAO, усредненных на различных временных интервалах. Временные серии не разбивались на отрезки условной монотонности, как при анализе трендов, а бралась вся имеющаяся в точке временная серия целиком. Результаты корреляционного анализа представлены в табл. 2. Уровень статистической достоверности приведенных КК различается: для минимальных величин КК p-значение (p-value) не превышает 0,1 (т. е. вероятность существования статистической связи более 90%), для относительно высоких КК (~ 0,5 и более) р-значение составляет 0,001 и менее (99,9% вероятности).
Из табл. 2 видно, что для каждой из временных серий имеется хотя бы один вариант усреднения индексов NAO, при котором связь со среднегодовыми SWH является статистически значимой на уровне a = 0,1. Наибольшие значения КК выделены жирным шрифтом и составляют 0,3–0,6. Чаще всего (во всех случаях, кроме точки 2) наибольшие значения КК соответствуют периоду усреднения индекса NAO с января по март (JFM). Этот результат совпадает с практикой использования данного интервала усреднения в научных исследованиях. Например, на сайте Центра прогноза климата США именно этому типу усреднения, как никакому другому, посвящена отдельная страница
Т а б л и ц а 2
T a b l e 2
Коэффициенты корреляции Пирсона и Спирмена, статистически
значимые для уровня a = 0,1 (90% вероятности)
Pearson and Spearman correlation coefficients statistically significant at level a = 0.1 (90% probability)
|
Точка / Point |
Период / Period |
КК / CC |
Y |
JFM |
ONDJFM |
DJFM |
NDJFM |
|
1 |
1949–1976 |
Пирсона (П.) / Pearson (P.) |
– |
0,31 |
– |
– |
– |
|
Спирмена (С.) / Spearman (S.) |
– |
0,29 |
– |
– |
– |
||
|
2 |
1966–2006 |
П. / P. |
0,29 |
- |
0,29 |
0,29 |
– |
|
С. / S. |
0,33 |
- |
0,32 |
0,34 |
– |
||
|
3 |
1979–1995 |
П. / P. |
– |
0,56 |
– |
– |
– |
|
С. / S. |
– |
0,58 |
0,48 |
– |
0,47 |
||
|
4 |
1979–2018 |
П. / P. |
0,41 |
0,60 |
0,31 |
– |
– |
|
С. / S. |
0,33 |
0,53 |
– |
– |
– |
||
|
5 |
1979–2018 |
П. / P. |
0,40 |
0,60 |
0,41 |
0,32 |
0,34 |
|
С. / S. |
0,40 |
0,51 |
0,37 |
0,31 |
0,30 |
||
|
6 |
1979–2018 |
П. / P. |
0,32 |
0,54 |
0,33 |
– |
– |
|
С. / S. |
0,35 |
0,49 |
0,29 |
– |
– |
||
|
7 |
1979–2018 |
П. / P. |
0,29 |
0,51 |
0,29 |
– |
– |
|
С. / S. |
0,34 |
0,47 |
– |
– |
– |
||
|
8 |
1979–2018 |
П. / P. |
– |
0,40 |
– |
– |
– |
|
С. / S. |
– |
0,39 |
– |
– |
– |
||
|
9 |
1979–2018 |
П. / P. |
0,34 |
0,53 |
0,37 |
0,28 |
0,28 |
|
С. / S. |
0,35 |
0,47 |
0,37 |
0,30 |
0,27 |
П р и м е ч а н и е. В столбце «Y» указаны КК между среднегодовыми SWH и среднегодовыми индексами NAO. Остальные столбцы содержат значения КК между среднегодовыми SWH и индексами NAO, усредненными для различных сочетаний холодных месяцев года: O – октябрь, N – ноябрь, D – декабрь, J – январь, F – февраль, M – март.
N o t e. The «Y» column indicates the CCs between the annual average SWH and the annual average NAO indices. The remaining columns contain the CC values between the annual average SWH and the NAO indices averaged for different combinations of cold months of a year: O – October, N – November, D – December, J – January, F – February, M – March.
Итак, расчеты показали, что межгодовые вариации NAO и среднегодовых SWH находятся в статистически значимой корреляционной связи. Второй момент, который важно было выяснить, какая статистическая связь более существенна – для годовых данных или данных с большим временным осреднением. С целью такой проверки дополнительно были рассчитаны КК между скользящими пятилетними средними для индексов NAO и среднегодовых SWH. Расчеты проводились во всех точках для тех случаев усреднения индексов NAO, которые дали наибольшие значения КК при анализе межгодовой изменчивости. Результаты сравнения корреляционной связи представлены в табл. 3.
Т а б л и ц а 3
T a b l e 3
Коэффициенты корреляции Пирсона и Спирмена между ежегодными
значениями индекса NAO и среднегодовыми SWH, а также между
их скользящими пятилетними средними
Pearson and Spearman correlation coefficients between the NAO index annual values and the SWH annual average values, as well as between their five-year moving averages
|
Точка / Point |
Период / Period |
КК / CC |
Ежегодные значения / Annual values |
Пятилетние средние / Five-year averages |
|
1 |
1949–1976 |
Пирсона (П.) / Pearson (P.) |
0,31 |
0,22 |
|
(JFM) |
Спирмена (С.) / Spearman (S.) |
0,29 |
0,38 |
|
|
2 |
1966–2006 |
П. / P. |
0,29 |
0,36 |
|
(DJFM) |
С. / S. |
0,34 |
0,41 |
|
|
3 |
1979–1995 |
П. / P. |
0,56 |
0,71 |
|
(JFM) |
С. / S. |
0,58 |
0,72 |
|
|
4 |
1979–2018 |
П. / P. |
0,60 |
0,83 |
|
(JFM) |
С. / S. |
0,53 |
0,82 |
|
|
5 |
1979–2018 |
П. / P. |
0,60 |
0,76 |
|
(JFM) |
С. / S. |
0,51 |
0,73 |
|
|
6 |
1979–2018 |
П. / P. |
0,54 |
0,65 |
|
(JFM) |
С. / S. |
0,49 |
0,58 |
|
|
7 |
1979–2018 |
П. / P. |
0,51 |
0,58 |
|
(JFM) |
С. / S. |
0,47 |
0,51 |
|
|
8 |
1979–2018 |
П. / P. |
0,40 |
0,54 |
|
(JFM) |
С. / S. |
0,39 |
0,50 |
|
|
9 |
1979–2018 |
П. / P. |
0,53 |
0,73 |
|
(JFM) |
С. / S. |
0,47 |
0,71 |
П р и м е ч а н и е. В столбце «Период» указан использованный вариант усреднения индекса NAO.
N o t e. The “Period” column specifies the option used for averaging the NAO index.
Из табл. 3 видно, что во всех случаях, кроме КК Пирсона для точки 1, КК для пятилетних средних больше, чем для годовых данных, т. е. межгодовые вариации SWH статистически менее значимо связаны с аналогичными вариациями NAO, чем более долгопериодные. Что касается пространственного распределения, обращает на себя внимание тот факт, что КК для точек в открытом море выше, чем для точек вблизи побережья. Кроме того, по-видимому, связь SWH с североатлантическим колебанием увеличивается с юга на север: самые высокие КК рассчитаны для точек 3, 4, 5 и 9, причем для самой северной точки 4 в Ботническом море связь самая сильная.
Связь SWH и NAO по годам, а также влияние пятилетнего усреднения на КК иллюстрирует рис. 2. Точки 4 и 9 выбраны в связи с тем, что для них разница между годовыми и пятилетними КК максимальна, 0,2 или выше.
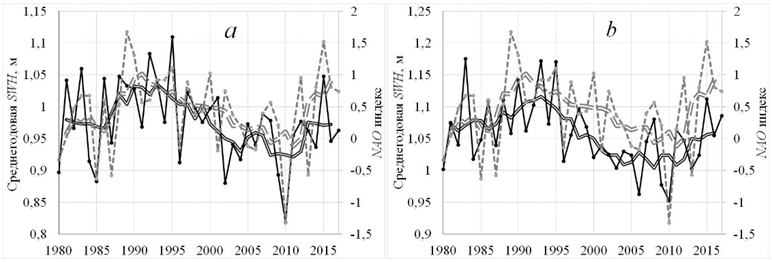
Р и с. 2. Осредненные среднегодовые SWH и индекс NAO с января по март (JFM) за период 1980–2017 гг. в точках 4 (a) и 9 (b). SWH: среднегодовые значения – тонкая сплошная линия, скользящее пятилетнее среднее – двойная сплошная линия; индекс NAO (JFM): ежегодный – штриховая линия, скользящее пятилетнее среднее – двойная штриховая линия
F i g. 2. Annual average SWH and NAO index averaged from January to March (JFM) for 1980–2017 at points 4 (a) and 9 (b). SWH: annual average values are indicated by a thin solid line, and 5-year moving average – by a double solid line; NAO index (JFM): annual value is indicated by a dashed line, and 5-year moving average – by a double dashed line
Из рис. 2 видно, что в значительной степени колебания среднегодовых SWH повторяют колебания годовых индексов NAO, что подтверждают и достаточно высокие КК для их межгодовых вариаций. Если сравнивать скользящие средние, то легко заметить, что до начала 90-х гг. наблюдается рост как индексов NAO, так и среднегодовых SWH. С начала 90-х гг. примерно до 2010 г. имеет место снижение как среднегодовых SWH, так и индексов NAO. Наконец, после 2010 г. наблюдаются тенденции к росту обоих параметров. Анализируя результаты, представленные на рис. 2 и в табл. 3, можно заключить, что индексы NAO и среднегодовые SWH коррелируют как в рамках межгодовой изменчивости, так и на более длительных временных интервалах.
Принимая во внимание коэффициент детерминации (квадрат величины коэффициента корреляции), показывающий в общем виде, какую часть изменчивости анализируемой переменной (характеристика волнения) можно объяснить с помощью регрессионной модели ее зависимости от фактора NAO, приходим к выводу, что в нашем случае влияние NAO может объяснить ~ 30–65% изменчивости волновых характеристик как в рамках межгодовой динамики, так и на более продолжительных временных отрезках.
Авторы данной работы не делают попытки физического объяснения механизма воздействия NAO на высоту волн в Балтийском море. В работе оценена связь и, главное, проведена оценка ее статистической значимости, что позволяет, опираясь на эти оценки, обсуждать возможные механизмы связи (или заявлять о их незначительности).
Выводы
1. Тенденции к росту и снижению среднегодовых SWH в Балтийском море чередуются. Продолжительность каждой из фаз условной монотонности составляет ~ 20 лет. За период с середины ХХ в. до 20-х гг. ХХI в. тенденции сменились три раза.
2. Отмеченные тенденции являются статистически значимыми на уровне a = 0,1 (90% вероятности) по крайней мере в некоторых точках моря. Скорости изменения среднегодовых SWH малы и могут составлять 5–20 мм/год в зависимости от пространственного положения точек.
3. Корреляционная связь между индексом NAO и среднегодовыми высотами волн статистически значима на уровне как минимум 90% вероятности, но не высока. Этим влиянием можно объяснить ~ 30–65% изменения волновых характеристик как в рамках межгодовой изменчивости, так и на более продолжительных временных отрезках.
4. Предпочтительным вариантом усреднения индекса NAO, обеспечивающим наибольшую корреляцию со среднегодовыми SWH, в большинстве случаев является усреднение с января по март (JFM).
1. Trends and extremes of wave fields in the north-eastern part of the Baltic Proper / B. Broman [et al.] // Oceanologia. 2006. Vol. 48. P. 165–184.
2. Режим, диагноз и прогноз ветрового волнения в океанах и морях / Под ред. Е. С. Несте-рова. Москва : Гидрометеорологический научно-исследовательский центр Российской Федерации, 2013. 292 с.
3. Tuomi L., Kahma K. K., Pettersson H. Wave hindcast statistics in the seasonally ice-covered Baltic Sea // Boreal Environment Research. 2011. Vol. 16, iss. 6. P. 451–472.
4. Soomere T. Numerical simulations of wave climate in the Baltic Sea: a review // Oceanologia. 2023. Vol. 65, iss. 1. P. 117–140. https://doi.org/10.1016/j.oceano.2022.01.004
5. Suursaar Ü., Kullas T. Decadal variations in wave heights near the Cape Kelba, Saaremaa Island, and their relationships with changes in wind climate // Oceanologia. 2009. Vol. 51, iss. 1. P. 39–61. https://doi.org/https://doi.org/10.5697/oc.51-1.039
6. Soomere T. Extending the observed Baltic Sea wave climate back to the 1940s // Journal of Coastal Research. 2013. Vol. 65, sp. iss. 2. P. 1969–1974. https://doi.org/10.2112/SI65-333.1
7. Cieślikiewicz W., Paplińska-Swerpel B., Soares C. G. Multi-Decadal Wind Wave Modelling over the Baltic Sea // Coastal Engineering : Proceedings of the 29th International Conference. Lisbon, Portugal : World Scientific Publishing Company, National Civil Engineering Labora-tory, 2005. P. 778–790. https://doi.org/10.1142/9789812701916_0062
8. Соколов А. Н., Чубаренко Б. В. Временнáя изменчивость параметров ветровых волн в Балтийском море за период 1979–2018 годов по результатам численного моделирова-ния // Морской гидрофизический журнал. 2020. Т. 36, № 4. С. 383–395. EDN SGVSPH. https://doi.org/10.22449/0233-7584-2020-4-383-395
9. Sokolov A., Chubarenko B. Baltic sea wave climate in 1979–2018: Numerical modelling results // Ocean Engineering. 2024. Vol. 297. 117088. https://doi.org/10.1016/j.oceaneng.2024.117088
10. Нестеров Е. С. Североатлантическое колебание: атмосфера и океан. Москва : ООО «Триада», 2013. 127 с. EDN UYJKZB.
11. Bacon S., Carter D. J. T. A connection between mean wave height and atmospheric pressure gradient in the North Atlantic // International Journal of Climatology. 1993. Vol. 13, iss. 4. P. 423–436. https://doi.org/10.1002/joc.3370130406
12. Bauer E. Interannual changes of the ocean wave variability in the North Atlantic and in the North Sea // Climate Research. 2001. Vol. 18, iss. 1–2. P. 63–69. https://doi.org/10.3354/cr018063
13. Woolf D. K., Challenor P. G., Cotton P. D. Variability and predictability of the North Atlantic wave climate // Journal of Geophysical Research: Oceans. 2002. Vol. 107, iss. C10. 3145. https://doi.org/10.1029/2001JC001124
14. Dodet G., Bertin X., Taborda R. Wave climate variability in the North-East Atlantic Ocean over the last six decades // Ocean Modelling. 2010. Vol. 31, iss. 3–4. P. 120–131. https://doi.org/10.1016/j.ocemod.2009.10.010
15. Różyński G. Long-term evolution of Baltic Sea wave climate near a coastal segment in Poland; its drivers and impacts // Ocean Engineering. 2010. Vol. 37, iss. 2–3. P. 186–199. https://doi.org/10.1016/j.oceaneng.2009.11.008
16. Surkova G. V., Arkhipkin V. S., Kislov A. V. Atmospheric circulation and storm events in the Baltic Sea // Open Geosciences. 2015. Vol. 7, iss. 1. 20150030. https://doi.org/10.1515/geo-2015-0030
17. Long-term Statistics of Storms in the Baltic, Barents and White Seas and Their Future Climate Projections / S. Myslenkov [et al.] // Geography, Environment, Sustainability. 2018. Vol. 11, iss. 1. P. 93–112. https://doi.org/10.24057/2071-9388-2018-11-1-93-112
18. Spatial and temporal wave climate variability along the south coast of Sweden during 1959–2021 / A. Adell [et al.] // Regional Studies in Marine Science. 2023. Vol. 63. 103011. https://doi.org/10.1016/j.rsma.2023.103011
19. Sen P. K. Estimates of the Regression Coefficient Based on Kendall’s Tau // Journal of the American Statistical Association. 1968. Vol. 63, iss. 324. P. 1379–1389. https://doi.org/10.1080/01621459.1968.10480934
20. Mann H. B. Nonparametric Tests Against Trend // Econometrica. 1945. Vol. 13, iss. 3. P. 245–259. https://doi.org/10.2307/1907187
21. Kendall M. G. Rank Correlation Methods. London : Charles Griffin, 1975. 202 p.
22. Jones P. D., Jonsson T., Wheeler D. Extension to the North Atlantic oscillation using early instrumental pressure observations from Gibraltar and south-west Iceland // International Journal of Climatology. 1997. Vol. 17, iss. 13. P. 1433 – 1450. https://doi.org/10.1002/(SICI)1097-0088(19971115)17:13%3C1433::AID-JOC203%3E3.0.CO;2-P
23. Hurrell J. W. Decadal Trends in the North Atlantic Oscillation: Regional Temperatures and Precipitation // Science. 1995. Vol. 269, iss. 5224. P. 676–679. https://doi.org/10.1126/science.269.5224.676
24. Rodwell M. J., Rowell D. P., Folland C. K. Oceanic forcing of the wintertime North Atlantic Oscillation and European climate // Nature. 1999. Vol. 398. P. 320–323. https://doi.org/10.1038/18648
25. Post E., Stenseth N. C. Climatic Variability, Plant Phenology, and Northern Ungulates // Ecology. 1999. Vol. 80, iss. 4. P. 1322–1339. https://doi.org/10.1890/0012-9658(1999)080[1322:CVPPAN]2.0.CO;2
26. D'Odorico P., Yoo J. C., Jaeger S. Changing Seasons: An Effect of the North Atlantic Oscil-lation? // Journal of Climate. 2002. Vol. 15, iss. 4. P. 435–445. https://doi.org/10.1175/1520-0442(2002)015<0435:CSAEOT>2.0.CO;2
27. Kolstad E. W., O’Reilly C. H. Causal oceanic feedbacks onto the winter NAO // Climate Dy-namics. 2024. Vol. 62, iss. 5. P. 4223–4236. https://doi.org/10.1007s00382-024-07128-y
28. Zhang W., Jiang F. Subseasonal Variation in the Winter ENSO-NAO Relationship and the Modulation of Tropical North Atlantic SST Variability // Climate. 2023. Vol. 11, iss. 2. 47. https://doi.org/10.3390/cli11020047














