Введение

Взаимодействие атмосферы и океана является одной из важнейших проблем в области наук о Земле. Широкое разнообразие физических процессов, протекающих в обеих средах вблизи границы раздела, и их сложные взаимосвязи существенно затрудняют разработку достоверных моделей для описания структуры пограничных слоев. Большое количество исследований в этой области позволило достичь определенного прогресса в изучении механизмов обмена атмосферы и океана и разработать полезные модели для прогнозирования тех или иных физических характеристик в приводном слое атмосферы и в приповерхностном слое моря. Тем не менее динамическое взаимодействие моря и атмосферы продолжает оставаться недостаточно изученной областью в теории климата и погоды, поскольку развитые на сегодняшний день модели часто показывают значительное расхождение результатов расчетов и фактических данных, таких, например, как температура поверхностности океана и толщина перемешанного слоя [1].

Составная часть этой проблемы – достоверное описание интенсивности вертикального турбулентного обмена в верхнем пограничном слое моря. Граничащий с атмосферой слой океана испытывает динамическое и другие воздействия в широком диапазоне масштабов. Это приводит к появлению различных процессов, влияющих на турбулентный обмен в этом слое: дрейфовых течений, поверхностных волн, циркуляций Ленгмюра и т. д. Генерация турбулентности этими механизмами зависит от конкретной гидрометеорологической ситуации и меняется в широких пределах, что существенно усложняет теоретическое описание. Интенсивность перемешивания при этом сильно зависит от касательного напряжения ветра, характера волнения, наличия обрушивающихся волн и от вертикальной стратификации слоя.

Вертикальный турбулентный обмен играет определяющую роль в формировании полей температуры, солености и других растворенных химических веществ в водной толще, влияет на скорость реакции моря на различные природные и антропогенные воздействия. Многие особенности гидрологической структуры могут быть объяснены на основе информации о механизмах вертикального обмена, их интенсивности, пространственной и временной изменчивости.

Процессы на поверхности моря, связь между поверхностными гравитационными волнами, ветром и течениями в прилегающих пограничных слоях играют ключевую роль в глобальной климатической системе [2]. Современные исследования турбулентности в верхнем слое океана направлены в первую очередь на уточнение роли отдельных механизмов генерации турбулентности в различных гидрометеорологических условиях, причем особое внимание уделяется штормовым условиям и слабым ветрам, так как именно в этих диапазонах скорости ветра существующие модели плохо соответствуют натурным измерениям.

Важнейшими механизмами генерации турбулентности в верхнем слое океана являются неустойчивость вертикальных градиентов скорости в дрейфовых течениях, неустойчивость движений, индуцированных поверхностными волнами, и обрушения волн . В ряде моделей часто отдается предпочтение одному или двум механизмам, что не позволяет достаточно точно описывать турбулентный режим [3–6]. Это либо сдвиг скорости течения, либо поверхностные волны, либо обрушения волн совместно со сдвигом скорости. В многомасштабной модели [7] рассматриваются все три перечисленных выше механизма генерации, но в ряде случаев и она не дает хорошего совпадения с экспериментальными результатами. Одна из возможных причин этого – неполное представление об источниках турбулентности в исследуемом слое.

В работе [8] изучается структура поверхностного пограничного слоя океана в присутствии турбулентности Ленгмюра и стабилизирующих поверхностных тепловых потоков. Предлагаются диагностические модели для равновесного пограничного слоя и глубины перемешанного слоя в присутствии поверхностного нагрева. Изучение различий в измерениях с неподвижного основания и с помощью дрифтеров на поверхности океана с применением структурных функций выполнено в работе [9]. Структурные функции первого, второго и третьего порядка рассчитываются с использованием квазилагранжевых (дрифтерных) и эйлеровых данных.

При моделировании интенсивности вертикального турбулентного обмена в приповерхностном слое моря самое значительное расхождение между расчетными и измеренными значениями скорости диссипации турбулентной энергии в наших экспериментах наблюдалось при слабых ветрах и незначительном волнении. В этих случаях экспериментальные значения могли превышать рассчитанные по моделям [3–7] на два порядка и больше. По нашему предположению, в этом случае турбулизация в приповерхностном слое может происходить в результате локальных неустойчивостей основного горизонтального течения, поскольку число Рейнольдса в таких течениях на три – четыре порядка превышает критическое. Учет этого механизма, а также неустойчивостей, связанных с когерентными структурами, на наш взгляд, улучшит достоверность модельных расчетов.

Цель работы – развитие физических представлений о динамическом взаимодействии двух сред на малых и субмезомасштабах и создание объективной модели для описания турбулентного режима приповерхностного слоя моря.

Эксперименты и натурные данные

Сотрудниками отдела турбулентности Морского гидрофизического института РАН на протяжении ряда лет проводятся экспериментальные исследования процессов турбулентного перемешивания вблизи поверхности моря. Эксперименты ведутся на стационарной океанографической платформе Черноморского гидрофизического подспутникового полигона (ЧГПП) МГИ. Система сбора данных включает в себя широкий набор измерительных средств: измерители метеорологических параметров, включая скорость и направление ветра, струнный волнограф, измерители скорости течения (акустические и вертушечного типа), CTD-измерители, позиционный турбулиметр «Сигма-1» [10] и другие (рис. 1). Такой набор данных позволяет регистрировать необходимые параметры фоновых и пульсационных величин и получать объективную картину изменчивости гидрофизических полей на протяжении достаточно длительных промежутков времени. Собранные натурные данные используются для верификации модельных оценок вертикального распределения гидрологических величин и интенсивности турбулентности (скорости диссипации турбулентной энергии ε).

Поскольку турбулиметр «Сигма-1» может использоваться для измерений пульсаций скорости течения только частотой выше 0,1 Гц, более медленные колебания, влияющие в конечном итоге на скорость диссипации турбулентной энергии, предпочтительно регистрировать измерителями с соответствующей дискретностью. В данной работе основной акцент делался на спектральном и структурном анализе данных о скорости течения, полученных акустическими измерителями в двух точках, 1 и 5 (рис. 1), разнесенных приблизительно на 10 м, и данных о пульсациях вектора скорости, измеряемых комплексом «Сигма» 2 (рис. 1). Остальные приборы обеспечивали информацией о фоновых гидрометеорологических параметрах и состоянии поверхности моря. Дублирование отдельных измерительных средств позволяло проводить сверку регистрируемых величин и исключить пропуски в рядах данных вследствие сбоев каких-либо приборов. В различные экспедиционные периоды конфигурация системы сбора данных незначительно менялась.

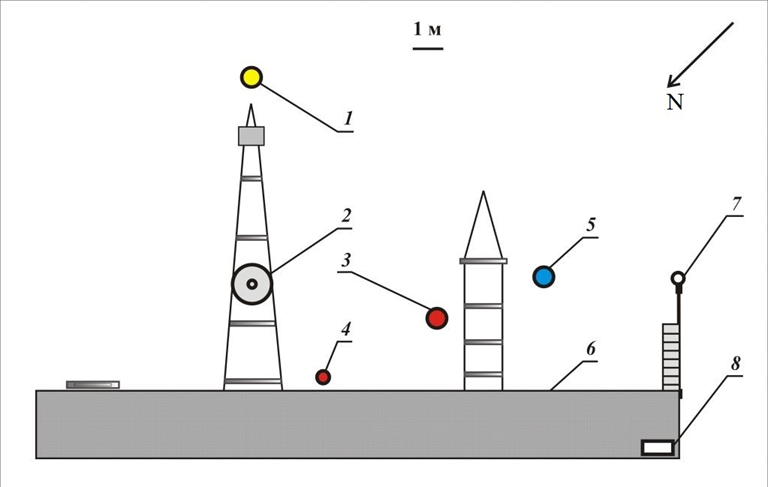
Р и с.  1. Схема расположения основных измерительных комплексов на океанографической платформе во время проведения экспериментов в мае – июне 2021 г.: 1 – акустический доплеровский профилограф DVS-6000; 2 – измерительный комплекс «Сигма-1»; 3 – измеритель скорости течения комплекс «Восток-М»; 4 – измерители течения МГИ-1308 (4 шт.); 5 – акустический доплеровский профилограф WorkНorse Monitor; 6 – океанографическая платформа; 7 – струнный волнограф; 8 – метеокомплекс

F i g.  1. Layout of the basic measuring systems at the oceanographic platform during the experiments in May – June 2021: 1 – DVS-6000 acoustic Doppler profiler; 2 – measuring system “Sigma-1”; 3 – current velocity meter “Vostok-M”; 4 – current meters MHI-1308 (4 pcs.); 5 – WorkHorse Monitor acoustic Doppler profiler; 6 – oceanographic platform; 7 – string wave recorder; 8 – meteorological system

Результаты измерений различными приборами подвергались предварительной обработке и первичному анализу: удалялись сбойные участки, неправдоподобные значения. Выбранные для анализа участки записей синхронизировались и приводились к одинаковой дискретности для совместной обработки. На рис. 2 приведен пример синхронизированных и приведенных к единому масштабу данных о модуле скорости течения, полученных с помощью измерения одновременно разными приборами (акустическими и вертушечными) в различных точках. Анализ осредненных данных показал, что разница значений модуля скорости течения, полученных в результате измерения акустическими комплексами, не превышает 5 %.

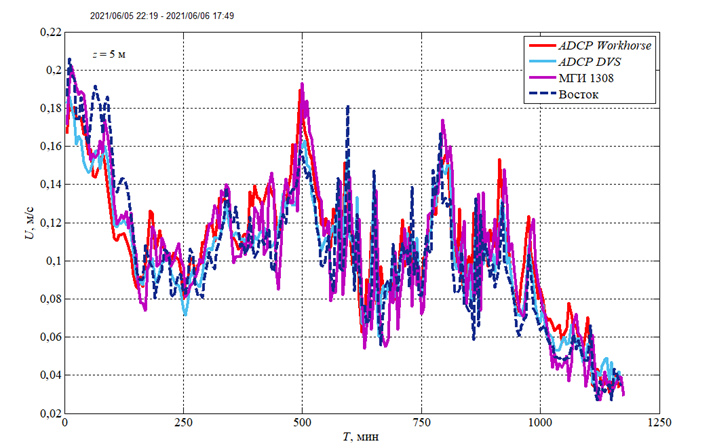
Р и с.  2. Модуль скорости среднего течения, по данным измерений различными приборами на глубине 5 м в районе океанографической платформы 5–6 июня 2021 г. Данные приведены к дискретности 5 мин

F i g.  2. Mean current velocity module based on measurements by various instruments at the 5 m depth in the area of the oceanographic platform on June 5–6, 2021. The data are reduced to a resolution 5 min

Кроме спектрального и структурного анализа измеренных величин применялся вейвлет-анализ для более точного выявления синхронной (асинхронной) изменчивости поля течений и идентификации когерентных структур. Вейвлет-анализ позволяет выявлять распределение энергии измеряемых величин по масштабам и прослеживать ее эволюцию [11]. Использовалось непрерывное вейвлет-преобразование

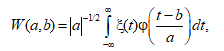
где W – вейвлет-коэффициенты; a – масштаб вейвлет-преобразования; b – сдвиг по оси времени; ξ – исходный сигнал; φ – материнский вейвлет; t – время. В качестве материнского, как правило, использовался вейвлет Морле

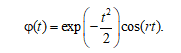
Глобальный спектр энергии в вейвлет-анализе является аналогом спектра мощности в гармоническом анализе, причем считается, что эта методика достоверно выявляет спектральные пики, хотя и уступает Фурье-преобразованию по спектральной разрешающей способности. Глобальный спектр рассчитывался по формуле

,

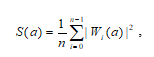где n – число отсчетов в ряду.

Основные соотношения

Представление турбулентных потоков в виде совокупности вихрей в результате последовательного распада больших на более мелкие, которые, в свою очередь, распадаются вплоть до самых мелких, диссипирующих в тепло, находит подтверждение в многочисленных экспериментальных работах. При описании турбулентности одним из важнейших теоретических предположений является гипотеза А. Н. Колмогорова о существовании инерционного интервала в спектре турбулентности [12]. Он показал, что структурная функция пульсаций скорости описывается универсальной зависимостью D ~ l^2/3, где l – расстояние между двумя точками измерений. Она не зависит от выбора начала координат вследствие статистической однородности пульсаций скорости и от направления разноса точек, а только от значения l, что является результатом статистической изотропности турбулентности. Для компонент вектора скорости, направленных вдоль l (продольная структурная функция),

Здесь  – структурный параметр, характеризующий скорость трансформации энергии вихря на единицу массы. Подобным образом рассчитывается температурный структурный параметр  (часто используется также термин «структурная характеристика») по разности температур в двух точках или структурный параметр показателя преломления в атмосфере  [13]. Расчет структурных функций и определение структурного параметра позволяет в нашем случае судить об уровне интенсивности турбулентности, обусловленной притоком энергии от локальных и когерентных вихрей в морских течениях. Из теории Колмогорова вытекает, что структурный параметр связан со скоростью диссипации турбулентной энергии, и в инерционном интервале спектра турбулентности , где c – константа .

С учетом гипотезы «замороженной турбулентности» Тэйлора структурную функцию рассчитывают и по измерениям в одной точке, вводя временной сдвиг τ:

При измерениях в фиксированных точках наличие структур в турбулентном потоке проявляется как заметное возрастание структурного параметра. Масштаб таких вихревых образований можно определить по спектру структурного параметра.

Для расчета интенсивности турбулентности и изменения ее с глубиной в приповерхностном слое моря разработана нестационарная модель [14], в которой базовыми уравнениями являются уравнения баланса импульса и турбулентной кинетической энергии. Как отмечалось ранее [7, 14], почти во всех моделях наблюдается значительное расхождение расчетов и экспериментальных данных при слабых ветрах и незначительном волнении. При этом генерация турбулентности в среднем переносном течении не рассматривается.

Для учета влияния когерентных структур и трансформации кинетической энергии течения в турбулентность вследствие локальных сдвигов скорости в настоящей работе предложено в уравнение баланса турбулентной кинетической энергии ввести дополнительный член , который описывает генерацию турбулентности этими вихревыми образованиями. В таком виде (изменение структурной функции во времени) слагаемое записано с точки зрения соответствия размерности (м²/с³), физический смысл этого слагаемого – описание притока энергии к турбулентности в уравнении баланса турбулентной энергии вследствие неоднородности течения.

Система исходных уравнений будет выглядеть таким образом:

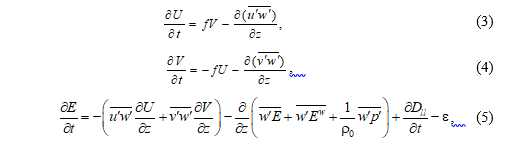
где: U и V – средние горизонтальные компоненты скорости вдоль осей x и y соответственно; f – параметр Кориолиса;  – пульсационные компоненты скорости;  – турбулентная кинетическая энергия; E^w – энергия поверхностного волнения;  – пульсации давления; ε – скорость диссипации. Замыкание системы осуществляется через соотношения, связывающие турбулентные потоки импульса с коэффициентом турбулентной вязкости:

где ν_t – коэффициент турбулентной вязкости; S_m – константа; l – турбулентный масштаб длины; ε – скорость диссипации. Масштаб l зависит от глубины как  z – глубина; z_b – обратное волновое число самых коротких обрушивающихся волн [6]; κ – постоянная Кармана; константа B = 16,6.

Начальные и граничные условия, как и метод решения, остаются такими же, как в работе [14]. На верхней границе

на нижней границе

                                                                                                                              ,   ,   .                                          

Структурная функция D_ll в модели параметризована обычной гармонической функцией с учетом эмпирических данных. Выписанная система уравнений (3)–(8) решалась численно методом прогонки.

Результаты

Относительно крупные когерентные структуры в приповерхностном слое моря наблюдаются на энергетических спектрах турбулентности. Пример Фурье-спектра среднеквадратических пульсаций скорости , осредненных по 5 мин, представлен на рис. 3. Исходные данные получены с дискретностью 100 Гц, затем обработаны фильтром верхних частот с порогом 1 Гц, чтобы исключить пульсации, связанные с поверхностным волнением. Спектры строились по методу Велча, при этом временной ряд разбивается на отрезки с перекрытием, они умножаются на временно́е окно Ханна, после чего осуществляется преобразование Фурье и последующее осреднение спектральных функций по всем отрезкам.

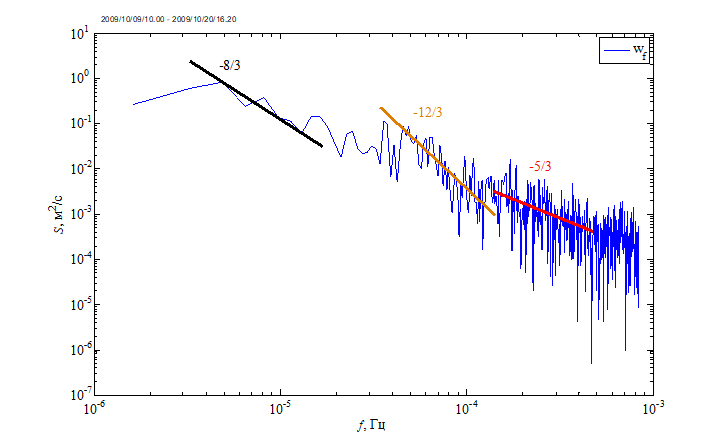
Р и с.  3. Спектр фильтрованных среднеквадратических пульсаций скорости, осредненных по 5 мин, в районе океанографической платформы, по данным измерений 9–20 октября 2009 г.

F i g.  3. Spectrum of filtered root-mean-square velocity fluctuations with 5-min averaging in the area of the oceanographic platform based on the measurement data obtained on October 9–20, 2009

Как видно из рисунка, спектр имеет сложную форму с различными наклонами в разных диапазонах. Как было показано в исследованиях атмосферной турбулентности [13, 15], когерентная турбулентность отличается от колмогоровской турбулентности более быстрым убыванием спектра (участки с наклоном −8/3 и −12/3), т. е. наличие таких участков в наших данных свидетельствует о существовании когерентных структур.

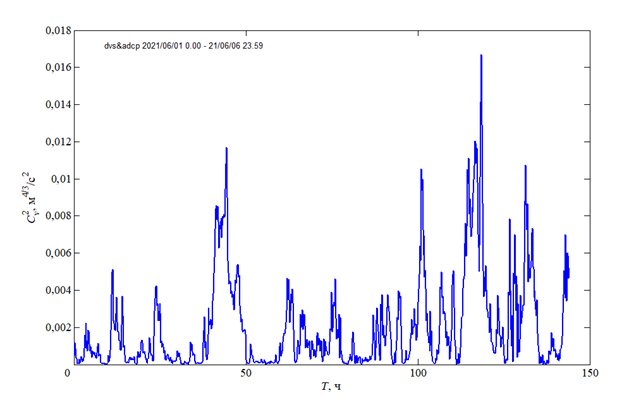
Р и с.  4. Продольный структурный параметр пульсаций скорости течения с осреднением по 10 мин на глубине 5 м в районе океанографической платформы 1–6 июня 2021 г.

F i g.  4. Longitudinal structural parameter of current velocity fluctuations with 10-min averaging at the 5 m depth in the area of the oceanographic platform on June 1–6, 2021

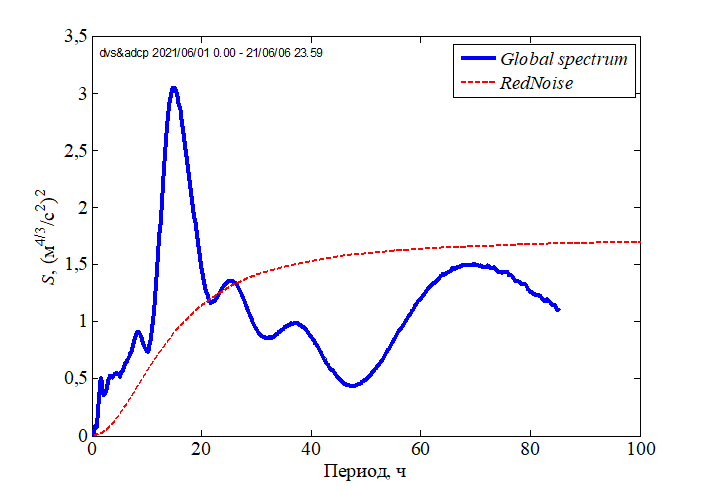
Р и с.  5. Глобальный спектр структурного параметра  за 1–6 июня 2021 г.

F i g.  5. Global spectrum of structural parameter for June 1–6, 2021

Основной массив данных, выбранных для анализа синхронных измерений скорости горизонтального течения в разнесенных точках и расчета структурных функций, получен в активный операционный период с 01.06.2021 по 06.06.2021 комплексами DVS-6000 и WorkНorse Monitor (3 и 8 на рис. 1). Фрагмент записей представлен выше на рис. 2. Структурные функции рассчитывались по соотношениям (1) и (2), во втором случае временной сдвиг варьировался от 5 мин до 1 ч. Изменчивость продольного структурного параметра  за указанный период приведена на рис. 4, глобальный спектр, рассчитанный с помощью вейвлет-анализа, – на рис. 5.

Как видно из рис. 5, в спектре существует ярко выраженный максимум на периоде ~ 15 ч, т. е. на отрезке времени протяженностью несколько суток такие структуры явным образом доминируют. Но если рассматривать менее длительные отрезки, в частности внутрисуточные колебания интенсивности пульсаций скорости, отчетливо прослеживаются масштабы с периодами 1,5 и 3,5 ч. Напомним, что значимыми на глобальном спектре считаются те максимумы, которые превышают уровень «красного шума». Вид спектра скорости течения отличается от спектра структурного параметра, что видно из рис. 6, где представлены нормированные на максимальное значение глобальные спектр  и спектр скорости течения, рассчитанный по значениям модуля скорости. Вклад течений в турбулизацию на бо́льших временны́х масштабах (пики ~ 40 и ~ 70 ч) был значительно ниже, чем на масштабе 15 ч, о чем можно судить по уровню спектральной функции.

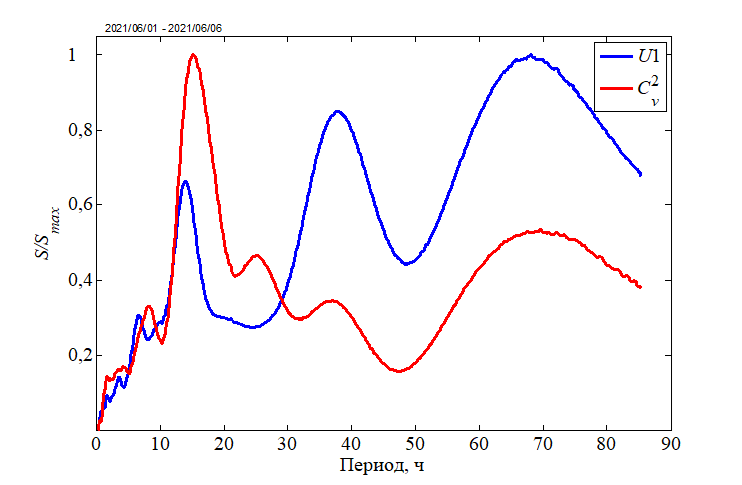
Р и с.  6. Нормированные глобальные спектры модуля скорости течения и структурного параметра за 1–6 июня 2021 г.

F i g.  6. Normalized global spectra of the current velocity module and structural parameter for June 1–6, 2021

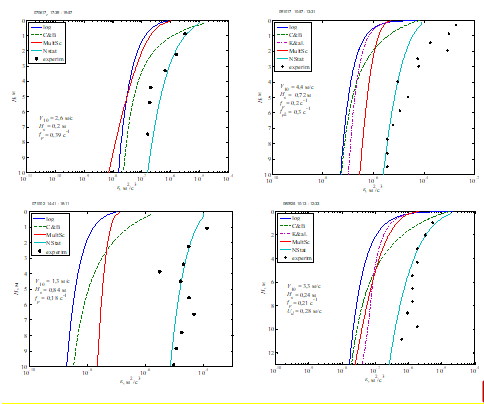
Р и с.  7. Модельные и экспериментальные значения скорости диссипации турбулентной энергии при слабом ветре. Обозначения: log – модель пристеночной турбулентности [4], C&B – модель [5], K&al. – модель [6]; MultSc – многомасштабная модель [7]; NStat – усовершенствованная нестационарная модель, точки – экспериментальные данные, V₁₀ – скорость ветра на высоте 10 м, H_S – высота значительных волн, f_p – частота спектрального пика волнения, U_d – скорость течения

F i g.  7. Model and experimental values of the turbulent energy dissipation rate at low wind. Designations: log is wall turbulence model [4], C&B is model [5], K&al. is model [6]; MultSc is multiscale model [7]; NStat is improved non-stationary model, points are experimental data, V₁₀ is wind speed at the 10 m height, H_S is height of significant waves, f_p is frequency of wave spectral peak, U_d is current velocity

Экспериментальные наблюдения, осуществляемые в течение ряда лет сотрудниками отдела турбулентности МГИ на океанографической платформе, позволили собрать обширные массивы информации о турбулентном режиме приповерхностного слоя в различных гидрометеорологических условиях. Данные о вертикальном распределении скорости диссипации турбулентной энергии дают хорошую возможность верификации различных моделей в широком диапазоне скорости ветра и разном характере волнения. Как уже говорилось, одним из недостатков моделирования вертикального турбулентного обмена в приповерхностном слое моря является расхождение рассчитанных и измеренных значений скорости диссипации при слабых ветрах. Сопоставление расчетов по усовершенствованной модели и натурных данных показало, что во многом эта проблема решается предложенным методом учета дополнительной турбулизации слоя с помощью структурной функции.

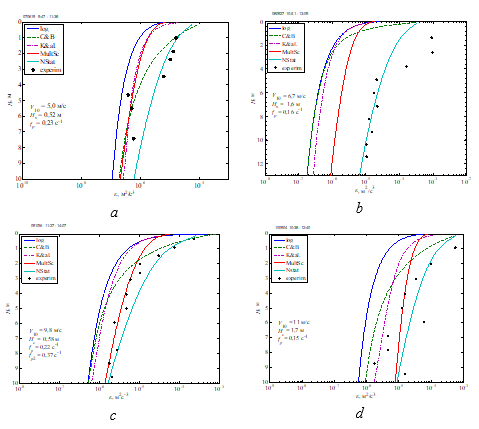
Р и с.  8. Модельные и экспериментальные значения скорости диссипации турбулентной энергии при умеренном (a, b) и сильном (c, d) ветре. Обозначения те же, что на рис. 7

F i g.  8. Model and experimental values of the rate of turbulent energy dissipation at moderate (a, b) and strong (c, d) winds. The designations are the same as in Fig. 7

На рис. 7 представлены экспериментальные данные о скорости диссипации при слабых ветрах и результаты расчетов по различным моделям, включая описанную в настоящей работе усовершенствованную нестационарную модель. Краткое описание моделей, использовавшихся для сопоставления, приведено в Приложении. Как видно из рисунков, введение дополнительного источника турбулентности через структурную функцию существенным образом улучшает соответствие расчетов и натурных измерений. На рис. 8 приведены примеры расчетов и экспериментальных данных при умеренных и сильных ветрах. Здесь для иллюстрации предпочтение было отдано случаям, когда другие модели недостаточно хорошо соответствовали экспериментам. Совпадение данных предложенной модели с результатами измерениями при таких условиях также вполне удовлетворительное.

Обсуждение

По современным представлениям, в турбулентных сдвиговых потоках характеристики переноса импульса, энергии и других величин определяются в большой степени крупномасштабным вихревым движением, а не хаотическим мелкомасштабным. Возникающие в турбулентном течении относительно крупные образования относят к когерентным структурам, называемым также детерминированными. По определению из работы [16, р. 307], «когерентная структура – это связанная турбулентная масса жидкости с мгновенно коррелированной по фазе завихренностью во всей ее пространственной области» . Важность параметризации этих структур обосновывается тем, что они могут переносить до 80 % от всей энергии турбулентного течения . В экспериментальных данных достаточно трудно разделить когерентную и некогерентную турбулентность, поскольку мелкомасштабная турбулентность (колмогоровская) присутствует и в самих когерентных структурах. На приведенном выше (см. рис. 3) спектре имеются участки, вполне точно соответствующие результатам работы [15], то есть наши измерения подтверждают сложный характер турбулентного течения и существование когерентных структур в исследуемом слое, поэтому описание турбулентного обмена требует дополнительного учета этого явления. Рассчитанная спектральная функция, на наш взгляд, достаточно объективно характеризует интенсивность турбулентности, обусловленную локальными неустойчивостями в морских течениях в прибрежной зоне.

Как следует из рис. 5, структуры с определенными масштабами могут доминировать в тех или иных условиях, что позволяет на данном этапе использовать модельное представление структурной функции достаточно простой зависимостью. В настоящей работе влияние когерентных структур на генерацию турбулентности параметризовано гармонической функцией с амплитудой и периодом, определенными по экспериментальным значениям продольной структурной функции (рис. 4), причем течение предполагалось однородным по вертикали. Происхождение и эволюция таких структур в зоне проведения экспериментов требует дальнейшего изучения, но весьма вероятно, что формирование вихрей в прибрежной зоне Крыма аналогично схеме, предложенной в работе [17]. По нашим оценкам, пространственные масштабы вихревых образований, влияющих значимым образом на генерацию турбулентности, составляют от нескольких сот метров до 4–6 км.

Выше отмечалось, что широко используемые модели для описания вертикального турбулентного обмена в верхнем пограничном слое моря сильно расходятся с наблюдениями при слабых и сильных ветрах, тогда как при умеренном ветре модели работают вполне удовлетворительно. При слабом ветре в наших экспериментах расхождения результатов расчетов по различным моделям и данных измерений могли составлять два порядка и более [7]. Расчет же по усовершенствованной нестационарной модели кардинально улучшает соответствие данных модели и результатов экспериментов для таких погодных условий (рис. 7).

Важно отметить, что приведенные экспериментальные данные собраны в различные годы и в различные сезоны, но в подавляющем числе экспериментов расхождения этих данных с модельными были незначительными. При умеренных и сильных ветрах модель также хорошо соответствует натурным измерениям (см. рис. 8), причем модельная константа для структурной функции оказалась достаточно универсальной, и модель хорошо работает примерно в 80 % рассмотренных случаев. Завышение модельных значений наблюдается при малой скорости течения 0,02–0,07 м/с, занижение – в отдельных случаях при штормовых условиях. Причины несоответствия требуют отдельного анализа всего комплекса гидрологических и метеорологических условий. Таким образом, можно сделать предварительный вывод, что влияние когерентных структур в турбулизации слоя становится доминирующим при слабом ветре, при умеренном и штормовом ветре их относительный вклад в генерацию турбулентности в самом верхнем слое моря уменьшается.

Заключение

Недостаточно полное описание сложных процессов обмена в верхнем пограничном слое моря влечет за собой неточности в прогнозировании таких важнейших параметров, как глубина перемешанного слоя и температура поверхности океана. В используемых в настоящее время климатических моделях рассматривается ограниченное число механизмов генерации турбулентности, определяющих интенсивность вертикального перемешивания, что нередко приводит к ощутимым различиям результатов расчетов и данных измерений.

В настоящей работе предложен усовершенствованный подход к описанию вертикального обмена в приповерхностном слое моря с введением в уравнение баланса турбулентной энергии члена, описывающего генерацию турбулентности когерентными структурами, образующимися в среднем течении. Физическим обоснованием такого подхода является представление о генерации турбулентности локальными неустойчивостями в потоке жидкости при больших числах Рейнольдса и сдвиговыми эффектами в относительно крупномасштабных вихревых структурах. Использование понятия структурной функции как характеристики трансформации энергии течения в турбулентность позволило получить весьма обнадеживающий результат, существенно улучшающий соответствие результатов расчетов и экспериментов в широком диапазоне гидрометеорологических условий. Количественное определение структурной функции и структурного параметра базируется на синхронном измерении скорости течения с помощью акустических измерителей в разнесенных по горизонтали точках. По глобальному спектру структурного параметра, рассчитанного с помощью вейвлет-анализа, выявлен доминирующий период колебаний интенсивности генерации турбулентности, который, по всей видимости, связан с существованием когерентных структур соответствующего масштаба в прибрежных морских течениях. Экспериментальные данные о временно́й изменчивости структурной функции параметризованы гармонической функцией, которая была встроена в модель.

Расчеты по предложенной модели показали кардинальное улучшение соответствия результатов расчетов с данными экспериментов при слабых ветрах, когда генерация турбулентности сдвигом скорости течения и поверхностным волнением незначительны. При умеренных и сильных ветрах модель также хорошо согласуется с натурными данными.

Приложение

Модели турбулентности, использовавшиеся для сопоставления

с предложенной нестационарной моделью

1. В модели, предложенной в работе [4], предполагается, что турбулентность под поверхностью океана аналогична турбулентности у твердой стенки. Скорость диссипации турбулентной энергии в этом случае рассчитывается в соответствии с формулой

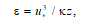
где  – динамическая скорость в воде; κ – постоянная  Кармана; z – глубина. Однако для применения такой аналогии, как отмечается в [4], необходимо правильно выбрать нулевую поверхность – фильтровать мелкие нерегулярные волны, а также правильно усреднять измеренные величины, чтобы получить структуру среднего течения, аналогичную турбулентному пограничному слою у плоской пластины. Часто эту модель называют логарифмической (по закону изменения скорости в турбулентном потоке вблизи твердой границы).

2. Одна из самых известных моделей турбулентности в приповерхностном слое разработана в работе [5], в которой для замыкания системы уравнений применяется гипотеза Прандтля о пути смешения. Эта модель показывает хорошее соответствие как натурным, так и лабораторным экспериментам [18, 19], причем результаты существенно зависели от величины параметра шероховатости z₀ и выбора масштаба турбулентности l. Слой у самой поверхности с повышенной скоростью диссипации трактовался как следствие потока турбулентной энергии от волн через поверхность.

В этой модели скорость диссипации и кинетическая энергия турбулентности определяются следующим образом:

где q – масштаб скорости; l – масштаб длины; B = 16,6 – константа; l = κ (z + z₀), z – глубина, z₀ – параметр шероховатости в воде, κ – постоянная Кармана. В модели получены как асимптотические аналитические решения, так и численные. Аналитически скорость диссипации выражается следующим образом:

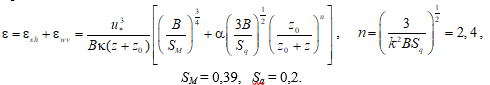
К настоящему времени эта модель является наиболее распространенной для описания турбулентности вблизи поверхности моря и часто используется для сопоставления с натурными и лабораторными экспериментами.

3. В модели Кудрявцева и соавторов [6] в качестве источников турбулентной энергии в самом верхнем слое моря принимаются сдвиг скорости и обрушение волн, в том числе и микрообрушения. Обрушение рассматривается как объемный источник энергии и импульса, зависящий от спектрального состава поверхностных волн. В уравнении баланса турбулентной энергии диффузией предлагается пренебречь. В отличие от модели из работы [5] параметр шероховатости z₀ в поверхностном слое в эту модель не входит. Численные расчеты по ней показали вполне удовлетворительное согласие с экспериментальными результатами из работы [20].

4. Многомасштабная модель турбулентности, разработанная автором [7], основана на разделении спектра турбулентности на участки, в которых генерация турбулентности происходит разными механизмами. Для каждого из участков составляется соответствующая система уравнений, основанная на k-ε модели. В качестве источников турбулентности рассматриваются сдвиг скорости дрейфового течения, нелинейные эффекты поверхностных волн и их обрушения. Для последних двух механизмов генерации предложены оригинальные параметризации. Предполагается также существование турбулентной диффузии волновой кинетической энергии. Модель показывает хорошее соответствие в широком диапазоне гидрометеорологических условий как собственным натурным данным, так и полученным другими авторами. Преимущество данной модели, по сравнению с другими аналогичными моделями, особенно наглядно проявляется в штормовых условиях.

1. A global perspective on Langmuir turbulence in the ocean surface boundary layer / S. E. Belch-er [еt al.] // Geophysical Research Letters. 2012. Vol. 39, iss. 18. L18605. https://doi.org/10.1029/2012GL052932

2. Sullivan P. P., McWilliams J. C. Dynamics of winds and currents coupled to surface waves // Annual Review of Fluid Mechanics. 2010. Vol. 42. P. 19–42. https://doi.org/10.1146/annurev-fluid-121108-145541

3. Csanady G. T. The free surface turbulent shear layer // Journal of Physical Oceanography. 1984. Vol. 14, iss. 2. P. 402–411. https://doi.org/10.1175/1520-0485(1984)014<0402:TFSTSL>2.0.CO;2

4. Benilov A. Yu., Ly L. N. Modelling of surface waves breaking effects in the ocean upper layer // Mathematical and Computer Modelling. 2002. Vol. 35, iss. 1–2. P. 191–213. https://doi.org/10.1016/S0895-7177(01)00159-5

5. Craig P. D., Banner M. L. Modeling of wave-enhanced turbulence in the ocean surface layer // Journal of Physical Oceanography. 1994. Vol. 24, iss. 12. P. 2546–2559. https:/doi.org/10.1175/1520-0485(1994)024<2546:MWETIT>2.0.CO;2

6. On the vertical structure of wind-driven sea currents / V. Kudryavtsev [et al.] // Journal of Physical Oceanography. 2008. Vol. 38, iss. 10. P. 2121–2144. https://doi.org/10.1175/2008JPO3883.1

7. Chukharev A. M. Multitime scale model of turbulence in the sea surface layer // Izvestiya, At-mospheric and Oceanic Physics. 2013. Vol. 49, iss. 4. P. 439–449. https://doi.org/10.1134/S0001433813040026

8. Langmuir turbulence and surface heating in the ocean surface boundary layer / B. Pearson [et el.] // Journal of Physical Oceanography. 2015. Vol. 45, iss. 12. P. 2897–2911. https://doi.org/10.1175/JPO-D-15-0018.1

9. Biases in structure functions from observations of submesoscale flows / J. Pearson [et al.] // Journal of Geophysical Research: Oceans. 2020. Vol. 125, iss. 6. e2019JCo15769. https://doi.org/10.1029/2019JC015769

10. Измерительный комплекс «Сигма-1» для исследования мелкомасштабных характеристик гидрофизических полей в верхнем слое моря / А. С. Самодуров [и др.] // Морской гид-рофизический журнал. 2005. № 5. С. 60–71. https:/doi.org/10.1007/s11110-006-0005-1

11. Астафьева Н. М. Вейвлет-анализ: основы теории и примеры применения // Успехи физи-ческих наук. 1996. Т. 166, № 11. С. 1145–1170. https:/doi.org/10.3367/UFNr.0166.199611a.1145

12. Колмогоров А. Н. Локальная структура турбулентности в несжигаемой вязкой жидкости при очень больших числах Рейнольдса // Доклады АН СССР. 1941. Т. 30, № 4. С. 299–303.

13. Атмосферная когерентная турбулентность / В. В. Носов [и др.] // Оптика атмосферы и океана. 2012. Т. 25, № 9. С. 753–759. EDN PCIOJL.

14. Chukharev A. M., Pavlov M. I. Turbulent Exchange in Unsteady Air–Sea Interaction at Small and Submesoscales // Izvestiya, Atmospheric and Ocean Physics. 2024. Vol. 60, iss. 1. P. 87–94. https://doi.org/10.1134/S0001433824700105

15. Причины проявления неколмогоровской турбулентности в атмосфере / В. П. Лукин [et el.] // Успехи современного естествознания. 2014. № 12. С. 369–377. EDN TENVOX.

16. Hussain A. K. M. F. Coherent structures and turbulence // Journal of Fluid Mechanics. 1986. Vol. 173. P. 303–356. https://doi.org/10.1017/S0022112086001192

17. Изменчивость поля течений в прибрежной зоне Черного моря по измерениям донной станции ADCP / А. Г. Зацепин [и др.] // Океанология. 2012. Т. 52, № 5. С. 629–642. EDN PCIKPJ.

18. Enhanced dissipation of kinetic energy beneath surface waves / Y. C. Agrawal [et al.] // Nature. 1992. Vol. 359. P. 219–220. https://doi.org/10.1038/359219a0

19. Cheung T. K., Street R. L. The turbulent layer in water at an air-water interface // Journal of Fluid Mechanics. 1988. Vol. 194. P. 133–151. https://doi.org/10.1017/S0022112088002927

20. Estimates of kinetic energy dissipation under breaking waves / E. A. Terray [et al.] // Journal of Physical Oceanography. 1996. Vol. 26, iss. 5. P. 792–807. https://doi.org/10.1175/1520-0485(1996)026<0792:EOKEDU>2.0.CO;2