УДК 574.58 Водные биоценозы
Цель. Разработка и применение комплексной математической модели для оценки экологическо-го воздействия устричной фермы на прибрежную акваторию Черного моря путем проведения модельных экспериментов, направленных на изучение процессов взаимодействия морских хо-зяйств с окружающей средой, – цель настоящего исследования. Методы и результаты. Имитационное моделирование устричной фермы в заливе Донузлав проводилось при помощи двухмерной химико-биологической объектно-ориентированной моде-ли морской экосистемы. В численных экспериментах имитировалось функционирование устрич-ной фермы мощностью ~ 100 т сырого веса и площадью 80 га, расположенной в центральной части зал. Донузлав. Расчеты для устриц первого, второго и третьего года культивирования проводились для периода с мая по октябрь. Показано, что при небольшой массе моллюсков на первом этапе культивирования (1,2–4,5 г сырого веса мягких тканей) влияние фермы на мор-скую экосистему незначительно. Во второй и третий годы выращивания регистрируется повы-шение объемов донных отложений, источником которых является устричная плантация. Выводы. Результаты моделирования свидетельствуют о необходимости расчета конфигурации фермы и количества выращиваемых моллюсков с целью снижения оказываемого негативного влияния на акваторию. Полученные качественные и количественные характеристики жизнедея-тельности плоской устрицы сопоставимы с данными из разработанной ранее одномерной модели роста моллюска и натурными данными мониторинга культивирования европейской устрицы в зал. Донузлав.
европейская устрица, залив Донузлав, химико-биологическая модель, прибрежная экосистема, индивидуум-ориентированное моделирование
Введение
Активное выращивание марикультуры поднимает большое количество вопросов, связанных с функционированием в прибрежной зоне морских экосистем, которые характеризуются большим числом физических, химических и биологических процессов. Как следствие, компоненты прибрежных экосистем взаимодействуют друг с другом и с морской средой посредством множества прямых и обратных связей. Успешность морского хозяйства определяется тем, насколько хорошо объекты марикультуры интегрируют в экосистему, сложившуюся в выбранном морском районе. Это значит, что обмен веществом и энергией между марикультурой и средой должен обеспечить устойчивый рост культуры и не только не ухудшить, но и по возможности улучшить состояние самой экосистемы. Оценить вышеуказанные процессы взаимодействия можно при помощи комплексных экологических моделей с физической, химической и биологическими составляющими. Рассмотрим ряд существующих моделей, которые имитируют функционирование марикультуры во взаимодействии с окружающей средой.
В работе [1] представлены результаты исследования влияния марикультуры мидии Mytilus galloprovincialis на морскую среду, полученные при помощи математического моделирования. Авторы использовали основанную на теории динамического бюджета энергии популяционную модель, дополнив ее натурными данными по содержанию сестона и химическому составу тканей мидий. Данные были получены в 2006–2007 гг. на трех мидийных фермах, расположенных на территории Италии и Словении в Адриатическом море. Динамику потоков углерода, азота и фосфора оценивали в течение 10-месячного срока выращивания. Расчеты показали, что количество азота и фосфора, выделяемое мидиями в процессе жизнедеятельности в виде фекалий и псевдофекалий, в два и пять раз больше зафиксированного в структуре моллюсков соответственно. Полученные результаты свидетельствуют о необходимости комплексного подхода к вопросам размещения марикультуры, учитывающего влияние морского хозяйства на окружающую среду.
Исследование [2] посвящено оценке влияния стока р. Апалачикола (Флорида, США) на популяцию гигантской устрицы Magallana gigas. Авторы использовали трехмерную гидродинамическую модель циркуляции и натурные данные, касающиеся жизненного цикла устрицы, для построения стохастических моделей. Результатом работы является определение ряда факторов среды, влияющих на динамику роста устриц. Было установлено, что главным фактором является гидрологический режим р. Апалачикола. Несмотря на детальное изучение процессов влияния морской среды на популяцию устриц, в исследовании остался неизученным вопрос о влиянии самой устричной фермы на экосистему акватории. Добиться более ясного понимания процессов, происходящих между марикультурой и средой, можно при объединении гидродинамической модели с биологической.
Работа [3] посвящена исследованию влияния устричной фермы на экосистему приливной зоны зал. Маренн-Олерон, Франция. Основное внимание уделено структуре пищевой цепи залива. Для исследования влияния устричной фермы на залив используется углеродная модель пищевой цепи. Анализ результатов показал, что присутствие устриц в экосистеме изменяет связи между бентосными и пелагическими организмами, что делает бентосных животных главными потребителями органического углерода. Увеличение площади устричной фермы в два раза привело к возрастанию вторичной продукции, которая стала пищей для молоди нектона. При помощи математического моделирования авторам удалось показать, как наличие марикультуры двустворчатых моллюсков в экосистеме может повлиять на видовой состав фауны приливной зоны. В процессе роста устрицы выделяют достаточно большие объемы аммония и фосфатов, однако в указанной работе не исследовалось прямое влияние этих соединений на экосистему.
Эффективность выращивания марикультуры часто оценивают при помощи показателя экологической емкости акватории. В работах [4–6] приведен ряд моделей, используемых для определения экологической емкости акватории, где расположены объекты марикультуры. В [4] представлена двухмерная физико-биогеохимическая модель, реализованная для зал. Сунго, Китай. Результаты [4, 7] и других работ были использованы при размещении морского хозяйства, выращивающего поликультуру в зал. Сунго. Несмотря на активную эксплуатацию залива в течение 60 лет, его экосистемы по-прежнему здоровы благодаря реализации научных рекомендаций по ведению морских хозяйств [8].
Анализ литературы показал широкое применение комплексных экологических моделей для исследования экосистем, включающих в себя марикультуру. Работы [1, 3, 6, 8] свидетельствуют о возможности применения таких моделей для оценки потоков нутриентов и углерода в экосистемах. Также комплексные экологические модели позволяют определять влияние гидрохимического режима на продуктивность культивируемых видов [2, 7, 9], прогнозировать экономическую прибыль [6, 8]. Анализ рассмотренных ранее моделей показал, что все они имеют географическую привязку и результаты моделирования существенно зависят от локальных условий. Перспективным является направление, при котором в качестве ядра биологического блока модели используется индивидуум-ориентированная модель культивируемого вида.
Цель исследования – разработка двухмерной модели морской прибрежной экосистемы с включением марикультуры европейской устрицы. На основе модели проводятся численные эксперименты для изучения и количественной оценки влияния устричной фермы на экосистему зал. Донузлав.
Материалы и методы
Предмет и объект исследования. Европейская устрица Ostrea edulis в прошлом веке являлась промысловым видом, однако ввиду большого сокращения численности утратила свое промысловое значение . Культивирование O. edulis представляет интерес в связи с актуальностью проблемы восстановления численности дикорастущей устрицы и выращивания в качестве марикультуры [10]. Объектом имитационного моделирования был выбран зал. Донузлав, в котором находится ряд действующих морских хозяйств по выращиванию мидии и устрицы [11]. Наличие натурных данных о динамике морфометрических характеристик плоской устрицы в этом районе 3 способствовало выбору зал. Донузлав в качестве района размещения модельной плантации.
Концепция модели. Двухмерная модель функционирования морской прибрежной экосистемы строится на принципах объектно-ориентированного моделирования (ООМ). Составляющими моделируемой экосистемы выступают морская среда, растительные и животные морские организмы. Ее компоненты моделируются в виде множества объектов или полей на регулярной сетке.
Объект ООМ определяется как совокупность идентичных организмов и их ближайшего жизненного пространства (БЖП), представленного, например, скоплением фитопланктона, небольшим участком дна, занятым макроводорослями определенного вида, коллектором мидий или садком устриц; БЖП – область, в которой протекают обменные процессы организмов и среды. Геометрически модельные объекты представляются в виде цилиндров, размеры которых соответствует реальным физическим размерам выделенного БЖП для совокупности морских организмов. Предполагается однородное распределение биомассы внутри объекта. Для цилиндра задается высота и радиус основания. Начальное положение объектов в пространстве модели можно выбирать или распределять случайным образом. При моделировании морских ферм объекты, которые имитируют выращиваемую марикультуру, располагаются в соответствии со схемой фермы. Объекты фитопланктона и фитобентоса распределяются случайным образом.
Размеры объектов могут изменяться с течением времени. Максимальный радиус горизонтальной проекции объекта задается равным шагу сетки. При превышении этого порогового значения происходит деление объекта на два новых, объем которых в сумме равен объему первоначального объекта. Масса делится поровну между новыми объектами.
Биомасса объекта может как увеличиваться в процессе роста, так и уменьшаться вследствие недостатка ресурсов. В целях экономии вычислительных мощностей в программе предусмотрена процедура удаления из расчетной области объектов с биомассой ниже порогового уровня. При этом биомасса объекта переходит в пул взвешенного органического вещества (POM).
Морская среда описывается совокупностью гидрофизических и гидрохимических полей, заданных на регулярной сетке. Управляющими переменными в модели выступают температура воздуха, скорость ветра и освещенность на поверхности моря. В модели рассчитываются концентрации неорганических соединений азота, фосфора и серы, POM и растворенного органического вещества (DOM), содержание в воде растворенного кислорода. Доступный объекту ресурс определяется как средневзвешенная величина значений в ячейках сетки, которые частично или полностью перекрывает горизонтальная проекция объекта. Весовые коэффициенты определяются пропорционально площади перекрытия объектом ячейки.
Разработанная имитационная модель функционирования прибрежной экосистемы позволяет получать количественные оценки характеристик среды и биологических объектов в любой момент времени. Такое представление дает возможность исследовать динамику всех параметров, которые определяют состояние прибрежной экосистемы, а также выявлять взаимосвязи между ее компонентами. Количественная оценка потоков вещества между компонентами экосистемы позволяет достаточно точно установить степень и характер влияния морского хозяйства на прибрежную экосистему.
ООМ морского хозяйства. На описанных выше принципах ранее была разработана двухмерная химико-биологическая объектно-ориентированная модель морского хозяйства [12]. Для имитации функционирования устричной фермы и процессов ее взаимодействия с морской средой в описание класса «Моллюски» был добавлен новый метод, разработанный на основе одномерной модели динамического энергетического баланса (ДЭБ) европейской устрицы [13], которая математически описывает процессы фильтрации, питания, дыхания, экскреции, роста и размножения устрицы. Результаты верификации модели показали хорошее соответствие значений расчетных величин линейного и весового роста устриц измеренным в ходе натурного эксперимента в зал. Донузлав в 2001–2003 гг. Рассмотрим более подробно структуру классов ООМ (рис. 1).
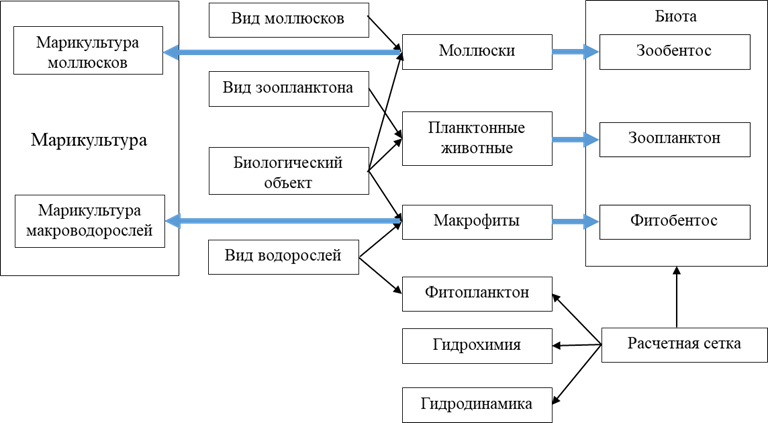
Р и с. 1. Схема классов химико-биологической объектно-ориентированной модели морской экосистемы. Черные стрелки обозначают наследование, голубые – включение множества объектов одного класса в свойства другого, более старшего класса
F i g. 1. Class diagram of the chemical-biological object-oriented model of marine ecosystem. Black arrows indicate heredity, blue ones – inclusion of multiple objects of one class into the properties of another higher class
«Расчетная сетка» – класс с координатами расчетной области и регулярной сеткой, в узлах которой задаются значения гидрофизических и гидрохимических переменных. Свойства класса: глубина водоема H, шаг сетки в dx (зональном) и dy (меридиональном) направлениях, размеры области Ndx ´ Mdy, границы водоема в пространстве, шаг по времени dt.
Класс «Гидродинамика» – наследник класса «Расчетная сетка». Основным методом класса является упрощенная интегральная модель верхнего слоя Черного моря [14, 15], которая описывает пространственно-временну́ю динамику температуры (T0, ℃) и глубины (h, м) верхнего перемешанного слоя, а также температуры нижнего слоя (Th, ℃). Указанные слои предполагаются однородными по плотности. Учитывая, что масштаб пространственной изменчивости полей ветра и температуры воздуха над морем (особенно в летний период) превышает размер расчетной области, используется одномерный вариант модели:
 ,
,
 ,
,
 (1)
(1)
 ,
,
где Г0 – поток тепла через поверхность; Гh-0 и Гh+0 – потоки тепла на нижней границе перемешанного слоя и верхней границе нижнего слоя соответственно; Та – температура воздуха (℃); a – коэффициент термического расширения воды; rw – плотность воды (кг/м3); G, D – интегральные генерация и диссипация энергии турбулентности;  – динамическая скорость трения в воде; t0 – напряжение трения ветра на поверхности; L – масштаб длины Монина – Обухова (м); L1 – масштаб толщины пограничного слоя (м); N = L/L1 – безразмерный параметр стратификации Казанского – Монина; Cg, а, а1, а2 – эмпирические коэффициенты.
– динамическая скорость трения в воде; t0 – напряжение трения ветра на поверхности; L – масштаб длины Монина – Обухова (м); L1 – масштаб толщины пограничного слоя (м); N = L/L1 – безразмерный параметр стратификации Казанского – Монина; Cg, а, а1, а2 – эмпирические коэффициенты.
Уравнение (1) определяет условие переключения между двумя режимами динамики верхнего слоя – вовлечения и антивовлечения части водной массы в верхний слой. Вовлечение происходит при G – D – 0,5rwaghГ0 > 0 (характеристики верхнего перемешанного слоя меняются, нижнего – нет). В обратном случае происходит антивовлечение (меняются характеристики нижнего слоя, верхний остается неизменным). Однако в результате газо- и теплообмена через поверхность температура и содержание кислорода в верхнем слое могут измениться. Таким образом, двухслойная модель с переменным во времени верхним слоем вносит дополнительное слагаемое в уравнения для гидрохимических переменных верхнего слоя [16]
и нижнего слоя
где Yi0 и Yih – переменные блока «Гидрохимия» в верхнем и нижнем слоях (мкМ); U, V – средние в слое скорости течения (м/с); Gi, Ai – функции источников (стоков), определяемые химическими и биологическими процессами соответственно; верхние индексы «0» и «h» определяют принадлежность члена верхнему или нижнему слою; H – глубина бассейна (м); Кх – коэффициент горизонтальной диффузии.
Класс «Гидрохимия» также является наследником класса «Расчетная сетка» и характеризуется следующими свойствами: концентрации нитратов, нитритов, фосфатов, растворенного кислорода, сероводорода, сульфатов, сульфитов, серы, растворенного и взвешенного органического азота в узлах регулярной сетки; коэффициенты в параметризациях химических реакций; коэффициенты диффузии для взвешенных и растворенных субстанций. Методы класса:
– одномерная химико-биологическая модель, совместно описывающая циклы азота и серы в аэробно-анаэробных условиях и разработанная для моделирования процессов в редокс-зоне Черного моря (обеспечивает задание функций Gi в уравнениях (2) и (3)). Уравнения химических реакций и значения параметров, использованных при расчетах, представлены в работе [17];
– процедура вычисления адвекции, диффузии и вертикального перемешивания на границе слоев с корректировкой гидрохимических переменных;
– процедура учета расхода и поступления растворенных и взвешенных веществ от биологических компонентов модели.
Класс «Фитопланктон» является наследником классов «Расчетная сетка» и «Вид водорослей». В настоящем варианте модели было использовано представление фитопланктона в виде пассивной примеси, что упрощает модель и экономит время счета при допустимой ошибке [18]. Основной метод этого класса – модель эволюции поля фитопланктона под воздействием внешних условий и взаимодействия с объектами марикультуры моллюсков. Она является двухмерным вариантом ранее разработанной и апробированной одномерной модели [19]:
 ,
,
где B – биомасса фитопланктона (мг/м3); t – время (сут); U, V – средние по вертикали скорости адвекции (м/с); m – максимальная удельная скорость валовой продукции фитопланктона (1/сут); Pr – реальная удельная скорость валовой продукции (1/сут); kr – коэффициент, определяющий затраты энергии на дыхание; ke – коэффициент выделения органического вещества (экссудации); m – скорость отмирания клеток фитопланктона (1/сут); QN и QP – внутреннее содержание азота и фосфора соответственно в клетках фитопланктона (пмоль/кл.); QNmax, QNmin, QPmax, QPmin – максимальное и минимальное содержание азота и фосфора в клетках фитопланктона (пмоль/кл.); [NO3], [NH4], [P] – концентрация нитратов, аммония и фосфора в воде (мкМ);
QN и QP – внутреннее содержание азота и фосфора соответственно в клетках фитопланктона (пмоль/кл.); QNmax, QNmin, QPmax, QPmin – максимальное и минимальное содержание азота и фосфора в клетках фитопланктона (пмоль/кл.); [NO3], [NH4], [P] – концентрация нитратов, аммония и фосфора в воде (мкМ);  ,
,  ,
,  – скорости изъятия нитратов, аммония и фосфора из воды (пмоль/(кл. сут));
– скорости изъятия нитратов, аммония и фосфора из воды (пмоль/(кл. сут));  ,
,  ,
,  – максимальные скорости изъятия нутриентов (пмоль/(кл. сут);
– максимальные скорости изъятия нутриентов (пмоль/(кл. сут);  ,
,  ,
,  – константы полунасыщения (мкМ);
– константы полунасыщения (мкМ);  – сумма воздействий на поле фитопланктона со стороны объектов устричной фермы. Число клеток фитопланктона в единице объема легко вычислить, зная содержание углерода в клетке QC, поскольку эта величина, в отличие от QN и QP, полагается постоянной. Для диатомовых QC = 12 пмоль/кл., B мг С/м3 = 0,083 ммоль С/м3, тогда число клеток
– сумма воздействий на поле фитопланктона со стороны объектов устричной фермы. Число клеток фитопланктона в единице объема легко вычислить, зная содержание углерода в клетке QC, поскольку эта величина, в отличие от QN и QP, полагается постоянной. Для диатомовых QC = 12 пмоль/кл., B мг С/м3 = 0,083 ммоль С/м3, тогда число клеток  .
.
Использованные в работе числовые параметры фитопланктона вида Thalassiosira pseudo представлены в табл. 1.
Т а б л и ц а 1
T a b l e 1
Значения параметров фитопланктона
Numerical values of phytoplankton parameters
|
Параметр / Parameter |
Thalassiosira pseudo |
|
QNmax, пмоль/кл. / QNmax, pmol/cell |
0,286 |
|
QNmin, пмоль/кл. / QNmin, pmol/cell |
0,050 |
|
QPmax, пмоль/кл. / QPmax, pmol/cell |
0,020 |
|
QPmin, пмоль/кл. / QPmin, pmol/cell |
0,001 |
|
|
0,257 |
|
|
0,744 |
|
|
0,210 |
|
|
0,580 |
|
|
0,860 |
|
|
0,200 |
|
kr, 1/сут / kr, 1/day |
0,150 |
|
ke, 1/сут / ke, 1/day |
0,250 |
|
m, 1/сут / m, 1/day |
0,250 |
|
Pmax, мг O2/г сух. вес/ч / Pmax, mg O2/g DW/h |
1,250 |
|
Rd, мг O2/г сух. вес/ч / Rd, mg O2/g DW/h |
0,310 |
|
α |
0,110 |
Свойствами класса «Биологический объект» являются координаты объекта в пределах области моделирования, вертикальный и горизонтальный размер, масса объекта, интервал возможных вариаций плотности и размеров объекта.
Свойства класса «Вид моллюсков» включают все необходимые параметры для описания энергетического баланса различных видов моллюсков. Класс «Моллюски» является дочерним по отношению к классам «Вид моллюсков» и «Биологический объект» и, таким образом, содержит полное описание носителя (коллектор или плот) с группой культивируемых моллюсков, включая набор параметров модели ДЭБ, которая описывает их рост на носителе и взаимодействие с окружающей средой. Основным методом класса «Моллюски» является модель ДЭБ соответствующего вида моллюсков [13]:
 ,
,
 ,
,
где Kd – калорийность тканей моллюска (кал/(г сух. вес)); Wd – сухой вес мягких тканей (г); Psom – энергетические затраты на рост соматических тканей (кал/ч); Pgen – энергетические затраты на рост генеративных тканей (кал/ч); Psh – энергетические затраты на рост раковины (кал/ч); R – энергия, затрачиваемая на дыхание моллюска (кал/ч); Ex – экскретируемая энергия (кал/ч); F – скорость фильтрации (л/ч); Kc – калорийность кормовой взвеси (кал/мг); С – концентрация кормовой взвеси (мг/л); Ae – коэффициент ассимиляции пищи.
В настоящий вариант экологической модели включены два варианта ДЭБ: для черноморской мидии Mytilus galloprovincialis и плоской устрицы Ostrea edulis. Таким образом, модель позволяет имитировать функционирование нескольких плантаций разных моллюсков в одном районе. Подробные модели ДЭБ, использованные для описания роста устриц и мидий, а также аппроксимации процессов жизнедеятельности, приведены в [13, 20].
Множество объектов класса «Моллюски» входит в состав класса «Марикультура». Этому классу присущи общие и интегральные характеристики морской плантации: ее конфигурация в пространстве, длина, объем, расположение коллекторов относительно поверхности, общая масса выращиваемых моллюсков, их продукционные характеристики, количество потребленных и выделенных веществ.
Аналогично объект класса «Моллюски» может описывать группу идентичных особей двустворчатых моллюсков, которая занимает фиксированную площадь дна с известными размерами и координатами. В этом случае множество таких объектов будет составлять массив «Зообентос».
Класс «Планктонные животные» является наследником классов «Биологический объект» и «Вид зоопланктона». Множество таких объектов («Зоопланктон» на рис. 1) вместе с массивами «Фитобентос» и «Зообентос» включается в класс «Биота», наследник класса «Расчетная сетка». В свойствах этого класса фигурируют поля всех биологических компонентов экосистемы на двухмерной сетке, а также средние или интегральные характеристики, необходимые для анализа поведения системы. Методы этого класса позволяют рассчитать все перечисленные характеристики и преобразовать представления в виде объектов в привычные двухмерные поля, удобные для анализа и визуализации.
Класс «Макрофиты» является наследником классов «Вид водорослей» и «Биологический объект» и, соответственно, в свойствах объектов этого класса содержится вся необходимая информация для расчета продукционных и метаболических процессов макроводорослей определенного вида. Основным методом класса «Макрофиты» является модель ДЭБ, разработанная в [21, 22]. Для макрофитов и микроводорослей используется практически одна и та же модель с некоторыми отличиями, обусловленными особенностями имеющихся натурных данных, на основе которых построены следующие уравнения:




 ,
,
где E0 (мкмоль фотон/м2/с) – фотосинтетически активная радиация (ФАР) на поверхности воды, E – на глубине z (м); Bm – биомасса объекта макрофитов (г сух. вес/м3); Pr – удельная скорость роста (1/сут); P(E) – скорость фотосинтеза (мг O2/г сух. вес/ч); Pmax – максимальная скорость фотосинтеза; α – наклон PЕ-кривой при малых значениях светового потока; Rd (мг О2/г сух. вес/ч) – темновое дыхание (характеризует количество кислорода, затраченного на дыхание в отсутствие потока ФАР); QN и QP (мкмоль/г сух. вес) – концентрации фосфора и азота в тканях водоросли; QNmax, QNmin, QPmax, QPmin (мкмоль/г сух. вес) – минимальные и максимальные концентрации фосфора и азота в тканях водоросли;  ,
,  ,
,  – скорости изъятия нитратов, аммония и фосфора из воды (мкмоль/г сух. вес/ч);
– скорости изъятия нитратов, аммония и фосфора из воды (мкмоль/г сух. вес/ч);  ,
,  ,
,  – максимальные скорости изъятия нутриентов;
– максимальные скорости изъятия нутриентов;  ,
,  ,
,  – константы полунасыщения (мкМ); m – коэффициент отмирания; ke – скорость экссудации; kDW – коэффициент пересчета мг О2 в мг С.
– константы полунасыщения (мкМ); m – коэффициент отмирания; ke – скорость экссудации; kDW – коэффициент пересчета мг О2 в мг С.
Использованные в работе числовые параметры фитобентоса, состоящего из двух видов морских трав (Zostera noltii и Ruppia maritima), представлены в табл. 2.
Множество объектов класса «Макрофиты» образует массив «Фитобентос», который является свойством класса «Биота». По аналогии с классом «Моллюски», множество объектов класса «Макрофиты» может входить в объект класса «Марикультура», который описывает плантацию выращиваемых макроводорослей. Самый старший класс «Экосистема» включает в себя экземпляры классов «Гидродинамика», «Гидрохимия», «Фитопланктон», «Марикультура», «Биота».
Т а б л и ц а 2
T a b l e 2
Значения параметров фитобентоса
Numerical values of phytobenthos parameters
|
Параметр / Parameter |
Zostera noltii |
Ruppia maritima |
|
QNmax, мкмоль/г сух. вес / QNmax, μmol/g DW |
4507 |
4507 |
|
QNmin, мкмоль/г сух. вес / QNmin, μmol/g DW |
755 |
755 |
|
QPmax, мкмоль/г сух. вес / QPmax, μmol/g DW |
118 |
118 |
|
QPmin, мкмоль/г сух. вес / QPmin, μmol/g DW |
30 |
30 |
|
|
3,0 |
14,1 |
|
|
19,4 |
75,0 |
|
|
2,42 |
9,30 |
|
|
1,5 |
1,5 |
|
|
7,0 |
9,2 |
|
|
12,3 |
12,3 |
|
ke, 1/ч / ke, 1/h |
0,1 |
0,1 |
|
m, 1/сут / m, 1/day |
0,005 |
0,005 |
|
Pmax, мг O2/г сух. вес/ч / Pmax, mg O2/g DW/h |
6,85 |
15,94 |
|
Rd, мг O2/г сух. вес/ч / Rd, mg O2/g DW/h |
1,70 |
1,43 |
|
α |
0,046 |
0,060 |
Результаты и обсуждение
Конфигурация модельной фермы подбиралась в соответствии с рекомендациями по ведению устричного хозяйства в зал. Донузлав 2. Общая площадь, занимаемая устричной плантацией, составляет ~ 80 га. Садки с устрицами подвешиваются на плоты. Каждый плот рассчитан на удержание 500 кг сырой массы устриц (включая раковину) товарного размера. Плоты последовательно соединены по 8 единиц в блок. Модельная устричная ферма состоит из 24 блоков, объем товарной продукции составляет ~ 100 т.
Начальные условия интегрирования: средний сухой вес мягких тканей одной устрицы и общий сухой вес всех культивируемых моллюсков на одном плоту (носителе), вертикальный профиль температуры воды, поля гидрохимических элементов (нитратов, нитритов, аммония, фосфатов, POM и DOM), биомасса фитопланктона. Поля соединений химических элементов формировались как случайные величины с заданным средним и дисперсией. Средние концентрации были взяты из работы [11]: [NH4] = 3,6 мкМ; [NO3] = 3,0 мкМ; [PO4] = 0,25 мкМ; [POM] = 5 мкмоль N/л; [DOM] = 5 мкмоль N/л; B = 200 мг/м3. В узлах сетки с дискретностью три часа были заданы векторы средних по вертикали скоростей течений, предварительно рассчитанные с использованием гидродинамической нелинейной сигма-координатной модели циркуляции вод в приближении гидростатики [23]. В данном варианте модели были выключены блоки зоопланктона и зообентоса.
На каждом шаге интегрирования вычислялись результаты процессов обмена объектов со средой. Фитопланктон и макроводоросли изымают из среды соединения углерода, азота и фосфора, выделяют кислород и DOM. Устрицы поглощают из среды фитопланктон и POM, а выделяют фосфаты, аммоний, DOM и РОМ (часть которого возвращается в пул взвешенного вещества в столбе воды, другая часть поступает в биоотложения (SDM)). Каждый последующий объект вычисляет доступные ресурсы на основе измененного состояния экосистемы, обусловленного предыдущими вычислениями. Таким образом имитируется конкуренция за ресурсы, и, если объекты пересекаются или накладываются друг на друга, потребление ресурсов предыдущими объектами на том же шаге по времени может оказаться значительным и часть объектов будет испытывать нехватку питательных веществ для роста. Очередность вычислений на каждом шаге интегрирования определялась для каждого объекта случайным образом, что предотвращало ситуацию, когда часть объектов находится в заведомо худших трофических условиях, чем остальные объекты.
Начальные и граничные условия. Шаг интегрирования различался для биологического, химического и динамического блоков. Динамика состояния биологических объектов и уравнения химических реакций рассчитывались с шагом три часа, адвекция и диффузия полей – с шагом 36 мин. На открытых границах расчетной области задавались условия равенства нулю градиента по нормали к границе.
Поле фитопланктона задавалось как множество объектов диатомовых микроводорослей с высокой скоростью роста. Управляющими переменными модели являлись освещенность на поверхности воды, температура воздуха и скорость ветра (рис. 2). Временной ряд освещенности поверхности задавался в соответствии со средними оценками инсоляции над Черным морем [24]. Суточная изменчивость моделировалась синусоидой, температура воздуха и скорость ветра – по данным ERA–Interim (2007 г.) с дискретностью три часа. Длительность интегрирования составила 5 мес с мая по октябрь – период активного роста устриц.
Время достижения устрицей товарного размера от момента ее посадки в садок для выращивания составляет 27–33 мес 2, поэтому расчеты проводились для двух размерных групп устриц, соответствующих второму и третьему годам культивирования с начальным сырым весом мягких тканей 2,3 г и 18,4 г (высота раковины 22 мм и 48 мм соответственно). Влияние устричной плантации на экосистему оценивали по динамике обменных процессов между устрицами и морской средой. В работе вычислялись средние по ферме высота устричной раковины, масса мягких тканей устрицы, скорости фильтрации, потребления, затраты на метаболизм, выделение, масса экскретируемых аммония и фосфатов, средние значения полей гидрохимических компонентов во всей расчетной области и в районе расположения устричной фермы.
Рассмотрим условия модельной морской среды, в которой выращиваются устрицы (рис. 2, 3). На рис. 3, a показано, как меняется вертикальный профиль температуры воды под воздействием прогрева и напряжения трения ветра. Профиль в соответствии с моделью ВКС определялся переменными T0, Th и h. Постепенно прогрев увеличивается, перемешивание достигает дна, после чего двухслойная структура фактически перестает существовать, устанавливаются условия однородности по всей глубине модельного водоема. Лишь при резком усилении ветра на короткое время возникает новый ВКС, который быстро исчезает. На рис. 3, b показаны динамика средней по расчетной области концентрации кормовой взвеси и соотношение между ее составляющими фитопланктоном и взвешенным органическим веществом (РОМ). Как видим, фитопланктон составляет примерно половину рациона моллюсков.
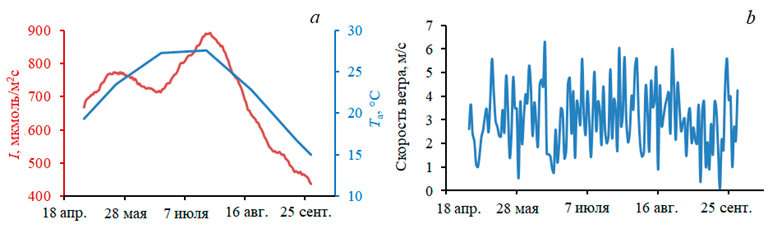
Р и с. 2. Управляющие переменные модели: инсоляция в полдень (красная кривая), максимальная за сутки температура воздуха (синяя кривая) (а); скорость ветра (b)
F i g. 2. Control variables of the model: insolation at midday (red curve), diurnal maximum air temperature (blue curve) (a); wind speed (b)

Р и с. 3. Условия морской среды: температура верхнего (синяя кривая) и нижнего (зеленая кривая) слоев воды, толщина верхнего слоя (а); концентрация кормовой взвеси и соотношение между составляющими рациона моллюсков – фитопланктоном и взвешенным органическим веществом (b)
F i g. 3. Marine environment conditions: temperature of the upper (blue curve) and lower (green curve) layers, thickness of the upper layer (a); concentration of suspended food, and ratio between the mollusc diet components: phytoplankton and suspended organic matter (b)
Численные эксперименты. Модель была верифицирована по данным из работы 3, полученным на устричной ферме в зал. Донузлав в 2002–2003 гг. При этом внешние условия эксперимента (температура воды и концентрация кормовой взвеси) примерно соответствовали реальным значениям. На рис. 4 показаны результаты сравнения натурных данных и модельных расчетов в периоды активного роста моллюсков второго и третьего годов культивирования.
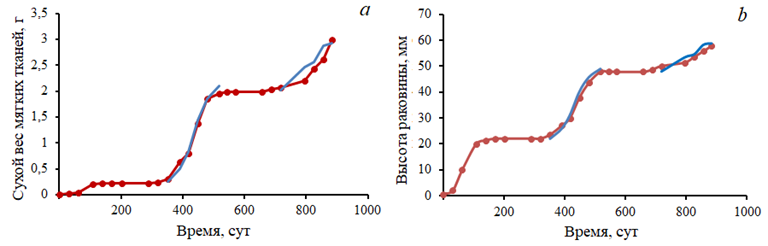
Р и с. 4. Сравнение модельных (синяя кривая) и натурных (согласно 3) (красная кривая) данных по двум показателям – сухому весу мягких тканей устрицы (а) и высоте раковины (b)
F i g. 4. Comparison of model (blue curve) and field (red curve) 3 data by two indicators: dry weight of oyster soft tissues (a) and shell height (b)
Все приведенные далее графики относятся к расчетам для третьего года культивирования, когда изменения в экосистеме более наглядны. Приведем средние по расчетной области значения основных гидрохимических характеристик, а также модельные данные о росте в течение 5 мес общей массы культивируемых устриц и соответствующего количества биоотложений (рис. 5). Как видно, концентрации в воде соединений азота и фосфора, как органических, так и неорганических, имеют определенные квазистационарные значения, которые слабо отличаются от полученных в расчете динамики экосистемы в отсутствие фермы. В районе непосредственного расположения фермы концентрации различаются на 10–20 %, а если рассматривать расчетную область в целом, то отличие не превышает 1–2 %. Различия в концентрациях химических компонентов наиболее заметны для органического вещества, поскольку неорганические соединения быстро поглощаются растительными составляющими экосистемы, а РОМ и DОМ остаются как следы функционирования автотрофов.
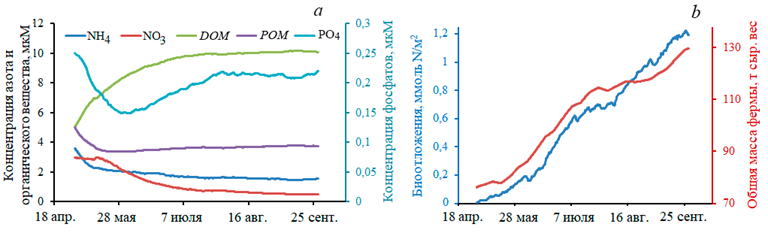
Р и с. 5. Графики динамики: гидрохимических характеристик для третьего года культивирования устриц (a), биоотложений и общей массы культивируемых устриц (b)
F i g. 5. Dynamic graphs of hydrochemical characteristics for the third year of oyster cultivation (a), biodeposits and total mass of cultivated oysters (b)
Функционирование устричной плантации общей массой ~ 100 т приводит к росту биоотложений и заиливанию дна не только непосредственно под фермой, но и на значительном удалении от нее (рис. 6).
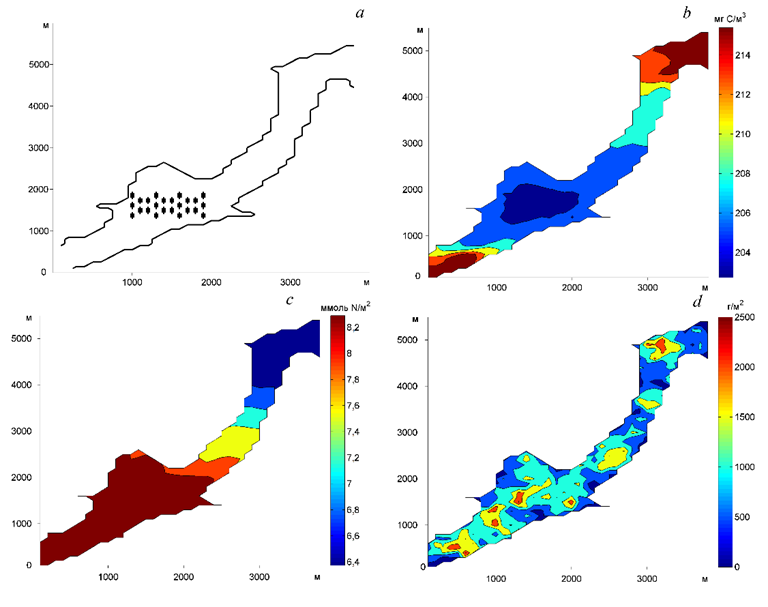
Р и с. 6. Схема устричной плантации (а), биомасса фитопланктона (b), биоотложения (c), биомасса фитобентоса (d). Поля показаны по состоянию на последний день расчета 30.09.2007 г.
F i g. 6. Oyster farm scheme (a), phytoplankton biomass (b), biodeposits (c), phytobenthos biomass (d). The submitted fields correspond to the last day of calculation on 30.09.2007
Как и следовало ожидать, в районе фермы биомасса фитопланктона ниже, чем в смежной акватории, однако это расхождение незначительно. Масса биоотложений растет к юго-западу, что, вероятно, обусловлено особенностями динамики вод.
Изучалось влияние фитобентоса на рост устриц и экологическое состояние акватории. Для этого сравнивались два расчета: при наличии фитобентоса (морские травы Ruppia maritima и Zostera noltii со средней общей биомассой 770 г сырого веса/м2) и в его отсутствие. Результаты представлены на рис. 7. Как показано, наличие донной растительности существенно снижает концентрацию неорганических соединений азота и фосфора, DOM и POM в акватории. При этом биомасса продукции фермы и количество биоотложений незначительно уменьшаются.
Положительное влияние зарослей морских трав на экологическое состояние прибрежных акваторий, особенно с затрудненным водообменом с открытым морем, хорошо известно. В первую очередь, фитобентос обеспечивает достаточное снабжение донных организмов кислородом, который расходуется на дыхание и окисление POM, оседающего на дно. Как показывают графики на рис. 7, он также снижает концентрацию соединений азота и фосфора в толще воды.
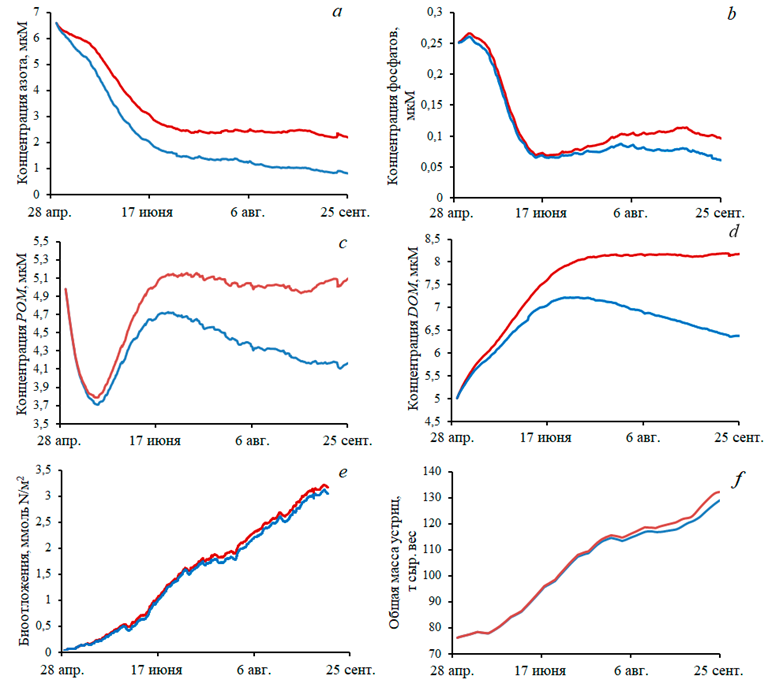
Р и с. 7. Сравнение двух численных экспериментов – с включением макрофитобентоса (синяя кривая) и без него (красная кривая): концентрация суммы аммония и нитратов в воде (а), фосфатов (b), РОМ (с), DOM (d), биоотложений в единицах азота (е), масса культивируемых на ферме устриц (f)
F i g. 7. Comparison of two numerical experiments – with (blue curve) and without (red curve) inclusion of macrophytobenthos: concentration of the sum of ammonium and nitrates in water (a), phosphates (b), POM (c), DOM (d), biodeposits in nitrogen units (e), mass of oysters cultivated at the farm (f)
Количество выделяемого устрицами азота в виде аммония составляет от 0,3 до 0,83 мг N/(г сух. вес сут), фосфора в виде фосфатов от 0,06 до 0,1 мг/(г сух. вес сут), органических соединений азота 0,03 мг N/(г сух. вес сут). На всей устричной ферме количество выделяемого азота составляет 0,33–1,35 кг N/сут и фосфора 0,04–0,18 кг Р/сут. В периоды нереста данные показатели удваиваются.
Заключение
Предложенная модель дает результаты, соответствующие натурным данным мониторинга выращивания плоской устрицы в зал. Донузлав и данным одномерной модели (линейной и весовой скорости роста, рациона, затрат на дыхание, экскрецию, продукцию). Динамика указанных характеристик определяется внешними условиями среды, такими как температура воды и концентрация кормовой взвеси, включающая РОМ и фитопланктон. Анализ результатов моделирования позволяет установить характер взаимодействия плантации моллюсков с акваторией и определить количественные характеристики обменных процессов. Устричная ферма включается в циклы углерода, азота и фосфора экосистемы, моллюски потребляют кормовую взвесь и выделяют детрит, аммоний и фосфаты. Модельные данные показывают, что в первый год культивирования (при среднем сыром весе мягких тканей моллюсков 1,2–4,5 г) влияние на экосистему незначительно. Однако при размерах моллюсков более 45 мм (17 г сырого веса мягких тканей) влияние фермы на экосистему становится заметным и усиливается по мере роста особей.
Концентрации растворенных соединений превышают фоновые в районе расположения фермы на ~ 10–20 %, однако в целом по заливу различия незначительны. Основное влияние устричной фермы – заиливание дна в результате осаждения биоотложений, таких как фекалии и псевдофекалии моллюсков. Область заиливания распространяется за пределы плантации, ее размеры и конфигурация определяются скоростью и направлением преобладающих течений. Фитобентос оказывает положительное влияние на качество воды в заливе, снижая концентрации аммония и фосфатов и конкурируя с фитопланктоном за питательные вещества, что подтверждается результатами численного моделирования.
1. An individual-based population dynamic model for estimating biomass yield and nutrient fluxes through an off-shore mussel (Mytilus galloprovincialis) farm / D. Brigolin [et al.] // Estuarine, Coastal and Shelf Science. 2009. Vol. 82, iss. 3. P. 365–376. https://doi.org/10.1016/j.ecss.2009.01.029
2. Modelling Oyster Population Response to Variation in Freshwater Input / R. J. Livingston [et al.] // Estuarine, Coastal and Shelf Science. 2000. Vol. 50, iss. 5. P. 655–672. https://doi.org/10.1006/ecss.1999.0597
3. Modeling the impact of oyster culture on a mudflat food web in Marennes-Oléron Bay (France) / D. Leguerrier [et al.] // Marine Ecology Progress Series. 2004. Vol. 273. P. 147–162. https://doi.org/10.3354/meps273147
4. Mathematical modelling to assess the carrying capacity for multi-species culture within coastal waters / P. Duarte [et al.] // Ecological Modelling. 2003. Vol. 168, iss. 1–2. P. 109–143. https://doi.org/10.1016/S0304-3800(03)00205-9
5. Review of recent carrying capacity models for bivalve culture and recommendations for re-search and management / C. W. McKindsey [et al.] // Aquaculture. 2006. Vol. 261, iss. 2. P. 451–462. https://doi.org/10.1016/j.aquaculture.2006.06.044
6. Ferreira J. G., Hawkins A. J. S., Bricker S. B. Management of productivity, environmental effects and profitability of shellfish aquaculture – the Farm Aquaculture Resource Management (FARM) model // Aquaculture. 2007. Vol. 264, iss. 1–4. P. 160–174. https://doi.org/10.1016/j.aquaculture.2006.12.017
7. A model for sustainable management of shellfish polyculture in coastal bays / J. P. Nunes [et al.] // Aquaculture. 2003. Vol. 219, iss. 1–4. P. 257–277. https://doi.org/10.1016/S0044-8486(02)00398-8
8. Polyculture of scallop Chlamys farreri and kelp Laminaria japonica in Sungo Bay / F. Jian-guang [et al.] // Chinese Journal of Oceanology and Limnology. 1996. Vol. 14, iss. 4. P. 322–329. https://doi.org/10.1007/BF02850552
9. Катрасов С. В., Бугаец А. Н., Жариков В. В. Оценка пространственной неоднородности условий культивирования тихоокеанской устрицы Magallana gigas (Thunberg, 1793) с помощью модели управления марифермами FARM в бухте Воевода (Японское море) // Биология моря. 2023. Т. 49, № 1. С. 37–44. EDN LRWITV. https://doi.org/10.31857/S0134347523010059
10. К вопросу организации крупномасштабного культивирования устриц в озере Донузлав / А. П. Золотницкий [и др.] // Труды ЮгНИРО. 2008. Т. 46. С. 48–54. EDN VSMAHB.
11. Современные гидрологический и гидрохимический режимы залива Донузлав / Н. Н. Дьяков [и др.]. Севастополь : Росгидромет, 2021. 464 с. EDN SYFWYC.
12. Vasechkina E. F. Coupled physical biological model of shellfish mariculture // Proceedings of the 13th International MEDCOAST Congress on Coastal and Marine Sciences, Engineering, Management and Conservation. MEDCOAST 2017. 2017. P. 381–392. EDN YVZFCD.
13. Филиппова Т. А., Васечкина Е. Ф. Имитационная модель роста устрицы Ostrea edulis L. в условиях культивирования // Экологическая безопасность прибрежной и шельфовой зон моря. 2023. № 4. С. 87–100. EDN NZYAOP.
14. Kraus E. B., Turner J. S. A One-Dimensional Model of the Seasonal Thermocline. II. The General Theory and Its Consequences // Tellus A: Dynamic Meteorology and Oceanography. 1967. Vol. 19, iss. 1. P. 98–106. https://doi.org/10.3402/tellusa.v19i1.9753
15. Васечкина Е. Ф., Тимченко И. Е., Ярин В. Д. Интегральная динамико-стохастическая модель деятельного слоя океана // Морской гидрофизический журнал. 1988. № 1. С. 16–22.
16. Моделирование интегральных процессов в морских экосистемах / В. Н. Еремеев [и др.] // Морской экологический журнал. 2007. № 1. С. 5–30. EDN UIQHCB.
17. Якушев Е. В., Михайловский Г. Е. Моделирование химико-биологических циклов в Бе-лом море. Расчет сезонной изменчивости фосфора, азота и кислорода // Океанология. 1993. Т. 33, № 5. С. 695–702.
18. Васечкина Е. Ф., Ярин В. Д. Сравнительный анализ экспериментов по моделированию морской экосистемы с использованием объектно-ориентированного подхода // Морской гидрофизический журнал. 2009. Т. 19, № 1. С. 26–35. EDN VOAIWT.
19. Vasechkina E. F. Nonlinear relationships between phytoplankton nutrient utilization traits and environmental factors // Ecological Modelling. 2020. Vol. 433. 109233. https://doi.org/10.1016/j.ecolmodel.2020.109233
20. Васечкина Е. Ф., Казанкова И. И. Математическое моделирование роста и развития ми-дии Mytilus galloprovincialis на искусственном субстрате // Океанология. 2014. Т. 54, № 6. С. 816–824. EDN TCJANB. https://doi.org/10.7868/S0030157414060112
21. Vasechkina E. Object-Based Modeling of Marine Phytoplankton and Seaweeds // Journal of Marine Science and Engineering. 2020. Vol. 8, iss. 9. 685. https://doi.org/10.3390/jmse8090685
22. Васечкина Е. Ф., Филиппова Т. А. Имитационное моделирование донного фитоценоза в прибрежной зоне Крыма // Морской гидрофизический журнал. 2020. Т. 36, № 3. С. 342–359. EDN NKQHDO. https://doi.org/10.22449/0233-7584-2020-3-342-359
23. Фомин В. В., Иванов В. А. Объединенная численная модель течений, волнения и транс-порта наносов озера Донузлав // Морской гидрофизический журнал. 2006. № 2. С. 43–65. EDN YOFQJN.
24. Изменчивость фотосинтетических параметров фитопланктона в поверхностном слое Черного моря / З. З. Финенко [и др.] // Океанология. 2002. Т. 42, № 1. С. 60–75. EDN ZVNYZV.




























