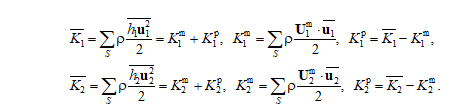Введение

Крупномасштабная циркуляция вод в Черном море, как считается, достаточно хорошо изучена научным сообществом. Период инструментальных наблюдений за течениями составляет более ста лет. Схема течений, основным элементом которой является меандрирующее Основное Черноморское течение (ОЧТ), расположенное по периметру глубоководной части моря, была впервые описана советским ученым Н. М. Книповичем в 1932 г. . Он предположил наличие внутри большого круговорота ОЧТ двух отдельных крупномасштабных циклонических вихрей, благодаря которым схема получила красивое название «очки Книповича». С тех пор эта схема циркуляции не подвергалась значительным изменениям, лишь уточнялась [1].

Кроме ОЧТ, элементами крупномасштабной циркуляции в Черном море являются вихревые образования – в основном антициклоны, которые формируются в ложбинах меандров между ОЧТ и берегом. Обычно их пространственный размер составляет 30–150 км. В научной литературе эти вихревые образования называются мезомасштабными вихрями, а ОЧТ – крупномасштабным течением. Однако, согласно классификации А. С. Монина , мезомасштабные вихри соответствуют процессам синоптической изменчивости, а ОЧТ – сезонной. Наиболее часто антициклонические вихри справа от ОЧТ, известные как квазистационарные Батумский и Севастопольский антициклоны [1], наблюдаются у восточного берега моря и к западу от Крымского п-ова.

Необходимо отметить, что все вышеперечисленные элементы крупномасштабной циркуляции существуют только в слое воды над главным пикноклином [2]. Перемещения водных масс, расположенных ниже пикноклина до самого дна, которые образуют глубинную циркуляцию, несмотря на длительный период наблюдений, изучены крайне слабо, поскольку проведение прямых измерений течений на больших глубинах и на длительный срок весьма трудоемко и дорого.

Отсутствие достаточного количества наблюдений привело к возникновению различных, часто противоречивых гипотез о силе и направлении глубинных течений. Одни из них предполагали полное их отсутствие, другие – разнонаправленность. Справедливости ради стоит отметить, что эпизодические измерения параметров течений на больших глубинах все же проводились. Результаты обработки данных наблюдений, собранных за много лет в Банке океанографических данных Морского гидрофизического института (БОД МГИ), можно найти в работе [3], из выводов которой следует, что в глубине Черного моря могут существовать течения переменного направления со скоростями до 25 см/с.

Научный прогресс не стоит на месте, и в XXI в. появились новые методы исследования глубоководных течений в Черном море. Во-первых, это буи Argo, которые запускают в Черном море с 1999 г. Они не измеряют непосред-ственно параметры течений, но позволяют рассчитать их траектории и средние скорости по перемещениям на определенной глубине.

После обработки большого массива данных буев Argo [4] был получен результат, который свидетельствует о том, что в среднем глубоководные течения движутся в циклоническом направлении вдоль изобат со скоростью 4–6 см/с. С учетом толщины слоя воды ниже пикноклина переносимая этими течениями масса воды оказывается больше массы, переносимой ОЧТ. Данное обстоятельство свидетельствует о том, что глубинные течения нельзя считать слабыми.

В 2016 г. учеными Института океанологии РАН и Морского гидрофизического института РАН на материковом склоне Черного моря была установлена долговременная буйковая станция, на которой в течение года с помощью доплеровского измерителя течений (ADCP) проводились измерения параметров течений в одной точке на глубине 1700 м [5]. Согласно этим измерениям, амплитуда колебаний горизонтальных составляющих скорости течений в глубине Черного моря составила ±15 см/с, что позволяет предположить наличие в поле течений волновых процессов.

Еще одним важным источником информации о течениях в Черном море являются результаты математического моделирования. Существует множество численных расчетов черноморской циркуляции, выполненных с помощью различных моделей [6–13]. Большинство из них успешно воспроизводят основные особенности крупномасштабной и мезомасштабной динамики моря в слое, расположенном выше главного пикноклина. Однако, когда речь заходит о глубинных течениях, полученных в численных моделях, авторы не всегда подробно их описывают и анализируют. При этом результаты, полученные разными авторами, могут существенно различаться как по величине скорости течений, так и по направлению глубинной циркуляции [11]. Кроме того, большое влияние на конечный результат может оказывать использование в моделях процедуры усвоения данных натурных наблюдений.

В работах [14–16], посвященных моделированию глубинной циркуляции в Черном море с помощью модели МГИ, основное внимание уделяется течениям над материковым склоном вдоль Кавказского побережья. В этой узкой области, расположенной на периферии глубинного слоя, периодически наблюдаются узкие струйные течения, направленные против основной циклонической циркуляции. При этом глубоководные течения в центральной части моря в этих работах описаны недостаточно полно, хотя скорости течений и толщина вовлеченного в движение слоя воды в этих областях значительно больше, чем на периферии.

Цель данной работы заключается в подробном описании и анализе полей глубинных течений, которые получаются в результате численного моделирования с использованием двухслойной вихреразрешающей модели, учитывающей реальный рельеф дна [17, 18]. Расчеты, проведенные с помощью данной модели, показали хорошее совпадение с реально наблюдаемой крупномасштабной циркуляцией в верхнем слое моря. Это объясняется тем, что в Черном море существует большой перепад плотности воды между поверхностными и глубинными водными массами, что позволяет рассматривать море как двухслойное [2]. Поскольку фактическая плотность воды в слое ниже основного пикноклина в Черном море меняется слабо [1], есть основания полагать, что глубинная циркуляция, рассчитанная с помощью двухслойной модели, может быть близка к реальной.

Одной из особенностей модели является учет рельефа дна, который оказывает значительное влияние на формирование глубинной циркуляции. Кроме того, упрощенная модель позволяет получить статистически равновесное решение, которое можно использовать для получения средних по времени оценок циркуляции и энергетических параметров течений.

Материалы и методы

Двухслойная модель. Выбор параметров. В модели рассматривается замкнутый водный бассейн, состоящий из двух однородных слоев жидкости с различной плотностью (ρ₁ < ρ₂). Уравнения двухслойной модели получаются интегрированием в пределах верхнего и нижнего слоя «примитивных» уравнений движения и неразрывности в декартовой системе координат с вертикальной осью Z, направленной вниз:

что позволяет ввести интегральную функцию тока ψ при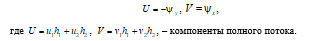 

Граничные условия на поверхности моря, поверхности раздела слоев и на дне учтены при выводе уравнений (1) – (4). На боковых границах задаются условия равенства нулю обеих компонент скорости течения (прилипание) и условие равенства нулю лапласиана скорости:

Параметр Кориолиса рассматривается в приближении β-плоскости. В модели учитываются придонное трение, трение между слоями и горизонтальная турбулентная вязкость, заданная бигармоническим оператором. Движение в модели возбуждается только касательным напряжением ветра. Потоки плавучести на поверхности моря и боковых границах не задаются, но баланс плавучести в модели учитывается наличием двух слоев различной плотности (граница между слоями имитирует постоянный пикноклин).

Конечно-разностная аппроксимация уравнений модели реализована на прямоугольной сетке B по терминологии Аракавы. Дивергентные члены в уравнениях движения и неразрывности аппроксимируются центральными разностями. Для интегрирования по времени используется полунеявная схема [19].

В экспериментах, результаты которых были использованы в данной работе, горизонтальный шаг сетки и шаг интегрирования по времени составили Δx = Δy = 2 км, Δt = 120 с соответственно. При заданном временном шаге интегрирования коэффициент бигармонической турбулентной вязкости A_B = = 1,5∙10⁸ м⁴/с обеспечивал устойчивость численной схемы.

Другие эмпирические параметры модели были заданы в соответствии с реальными параметрами Черного моря. Редуцированное ускорение свободного падения  , определяющее перепад плотности в слоях, соответствовало разнице в солености верхнего и нижнего слоев (ΔS = 4 ‰) и составило 0,032 м/с². Толщина верхнего слоя в состоянии покоя h₀ = 100 м.

Придонное трение принималось пропорциональным квадрату скорости течения, коэффициент трения определялся таким образом, чтобы скорости глубинных течений в модели соответствовали скоростям, приведенным в работах [4, 5].

Модельные поля касательного напряжения ветра на поверхности моря рассчитывались с помощью эмпирических формул, учитывающих особенности пространственной и временной изменчивости реальных полей ветра [20]. При этом среднегодовые значения завихренности касательного напряжения ветра попадали в диапазон значений, известных по наблюдениям [1].

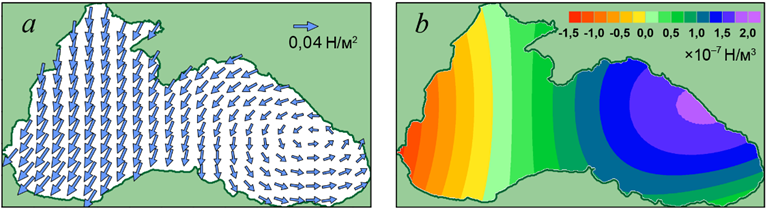
В качестве характеристик, позволяющих отслеживать ход численного эксперимента, использовались средние по акватории моря значения кинетической энергии в верхнем ⟨K₁⟩ и нижнем ⟨K₂⟩ слоях, которые определялись по формулам

 ,

где угловые скобки означают осреднение по площади всего моря; (u₁, v₁), (u₂, v₂) – горизонтальные составляющие скорости течений в верхнем и нижнем слое соответственно; h₁, h₂ – толщины слоев; ρ – средняя плотность воды в море.

Результаты численных экспериментов

Анализ пространственно-временной изменчивости полей глубинных течений осуществлялся по результатам трех численных экспериментов, проведенных с помощью описанной выше двухслойной модели. Эксперименты, обозначенные в работе как E1, E2, E3, различались между собой только величиной и периодичностью ветрового воздействия на морскую поверхность. Во всех экспериментах расчет начинался из состояния покоя, при котором уровень моря и граница раздела слоев считались горизонтальными, скорости течений равнялись нулю.

В эксперименте E1 поле касательного напряжения ветра задавалось стационарным по времени, но учитывающим особенности его пространственного распределения [20]. Как было показано в работе [21], эти особенности играют значимую роль для адекватного формирования крупномасштабной циркуляции. Цель эксперимента Е1 состояла в том, чтобы проследить этапы формирования циркуляции из состояния покоя до выхода решения в режим статистического равновесия. Кроме того, в результате экспериментов установлено, что при стационарных внешних условиях модель быстрее достигает режима статистического равновесия. Алгоритмически стационарное поле τ (x, y) = (τ^x, τ^y) рассчитывалось с помощью формул

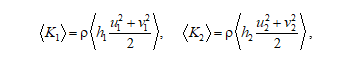             (1)

где  –  постоянные амплитудные значения;  – коэффициент, определяющий распространение зоны антициклонической завихренности на восток;  – параметр, определяющий временную изменчивость.

На рис. 1 приведены карты полей τ и rot_Z τ в эксперименте Е1. Для расчета τ в формуле (1) использовались значения , α = 0,85, S = 0,4. Согласно этому рисунку, завихренность τ имеет положительный максимум (соответствует циклону) в восточной части моря. В западной части моря расположена область с отрицательной (антициклонической) завихренностью τ.

Р и с.  1. Стационарные поля τ (a) и rot_Z τ (b) в эксперименте Е1

F i g.  1. Stationary fields τ (a) and rot_Z τ (b) in experiment E1

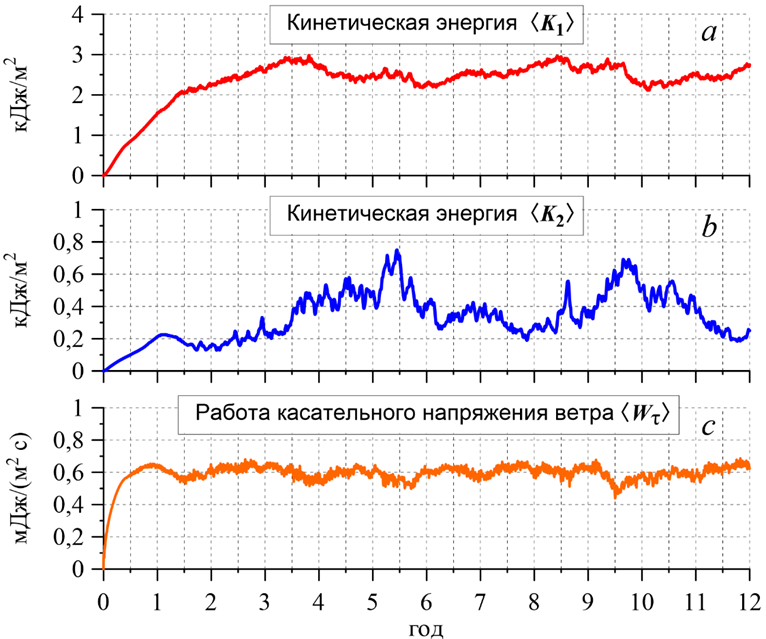
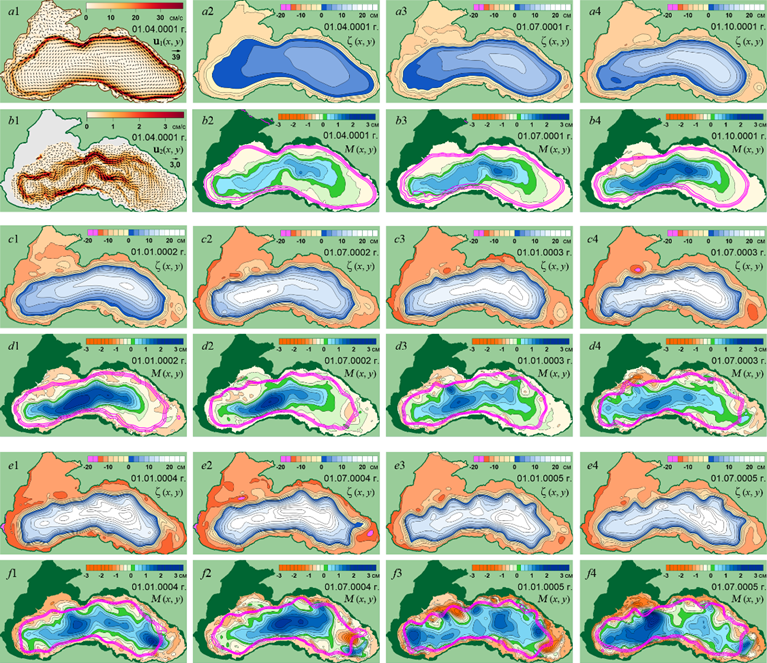
На графиках временной изменчивости ⟨K₁⟩ и ⟨K₂⟩, построенных для эксперимента Е1 (рис. 2, a, b), видно, что в течение первого года от начала расчетов кинетическая энергия течений растет как в верхнем, так и в нижнем слое моря. В это время под действием ветра с циклонической завихренностью в верхнем слое происходит формирование струи ОЧТ, которая располагается левее границы распространения нижнего (глубоководного) слоя (рис. 3, a1). В нижнем слое вследствие экмановской накачки [22] образуются течения, направленные преимущественно вдоль изобат (рис. 3, b1).

Р и с.  2. Зависимость от времени ⟨K₁⟩ (a), ⟨K₂⟩ (b), ⟨W_τ⟩ (с) в эксперименте Е1

F i g.  2. Time dependence of ⟨K₁⟩ (a), ⟨K₂⟩ (b) and ⟨W_τ⟩ (с) in experiment E1

Рядом с полями скорости течений (рис. 3, a1, b1) приведены соответствующие им поля уровня моря ζ и функции M (рис. 3, a2, b2). Функция  (аналогичная потенциалу Монтгомери в метеорологии) определяет давление воды в нижнем слое, так же как ζ определяет давление воды в верхнем слое.

Скалярные поля ζ и M удобно использовать для визуализации течений вместо векторных полей u₁, u₂, поскольку геострофическое равновесие позволяет рассматривать изолинии ζ в качестве линий тока течений верхнего слоя, а изолинии M – в качестве линий тока течений нижнего слоя. Течения направлены таким образом, чтобы более высокие значения ζ и M находились справа по направлению потока. Скорость течений при этом обратно пропорциональна расстоянию между изолиниями ζ, M.

Для удобства сопоставления течений в верхнем и нижнем слое на картах М розовым цветом показаны изолинии ζ, соответствующие стрежню ОЧТ.

Р и с.  3. Мгновенные поля u₁ (a1), u₂ (b1), ζ (a2 – a4, c1 – c4, e1 – e4), М (b2 – b4, d1 – d4, f1 – f4) в эксперименте Е1

F i g.  3. Instantaneous fields u₁ (a1), u₂ (b1), ζ (a2 – a4, c1 – c4, e1 – e4) and М (b2 – b4, d1 – d4, f1 – f4) in experiment E1

Карты ζ (x, y) и М (x, y) с датами 01.07.0001–01.01.0002 (рис. 3, a3, a4, b3, b4, c1, d1) показывают, что течения в верхнем (ОЧТ) и нижнем слоях усиливаются во время первого года, вызывая рост значений ⟨K₁⟩ и ⟨K₂⟩ (рис. 2, a, b).

Во второй год усиление ОЧТ (рис. 3, c2 – с4) и рост ⟨K₁⟩ продолжаются, а в нижнем слое, наоборот, происходит ослабление циркуляции (рис. 3, d2 – d4) и уменьшение ⟨K₂⟩. Такое поведение течений и кинетических энергий объясняется ослаблением работы касательного напряжения ветра ⟨W_τ⟩ после достижения его максимума в конце первого года (рис. 2, c). В результате, подъем границы раздела слоев, вызываемый экмановской накачкой, замедляется. Уменьшение ⟨W_τ⟩, в свою очередь, связано со спрямлением струи ОЧТ на востоке моря и ее перемещением из зоны с максимальной завихренностью касательного напряжения ветра (рис. 3, a4).

К концу второго года приток в море энергии от ветра стабилизируется и до конца расчетов остается в определенных пределах (рис. 2, c), что характерно для статистически-равновесного режима. К стабилизации ⟨W_τ⟩ приводят рост скорости поверхностных течений и неустойчивость ОЧТ, проявляющаяся в его меандрировании. Неустойчивость возникает в середине первого года и развивается в течение второго и третьего годов (рис. 3, a3, a4, с1 – с4).

Усиление неустойчивости ОЧТ приводит к образованию на периферии нижнего слоя (под ОЧТ) вихревых образований (ВО)  которые перемещаются над материковым склоном и материковым подножием в циклоническом направлении синхронно с меандрами ОЧТ (рис. 3, d1 – d4, f1 – f4). Наиболее интенсивно данный процесс происходит в северной половине моря.

В течение третьего и четвертого годов кинетическая энергия течений в двух слоях увеличивается (рис. 2, a, b). В нижнем слое рост энергии происходит за счет увеличения количества и размеров вихревых образований, формирующихся над материковым склоном и материковым подножием. К началу пятого года вихреобразование в нижнем слое достигает максимального развития (рис. 3, f3), соответствующего уровню поступающей в море ветровой энергии в режиме статистического равновесия.

Вихревые образования, образующиеся в нижнем слое моря, представляют собой возмущения в поле течений, перемещающиеся в пространстве, т. е. волны. По характеру проявления эти волны относятся к классу градиентно-вихревых [23], которые образуются вследствие выполнения закона сохранения потенциального вихря [24], имеющего для нижнего слоя двухслойной жидкости следующий вид:

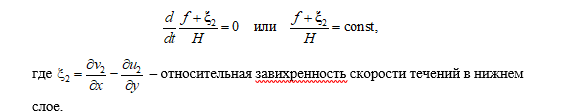
Согласно этому закону, если при перемещении водной массы происходит изменение параметра Кориолиса f и/или глубины моря H (x, y), то это приводит к изменению относительной завихренности движущейся воды ξ₂. В первом случае формируются планетарные волны Россби, во втором – захваченные наклонным дном волны (разновидность топографических волн Россби). В роли наклонного дна выступают материковый склон и материковое подножие.

Далее на примере экспериментов E2, E3 рассмотрим особенности формирования глубинной циркуляции в статистически равновесном режиме. В этих экспериментах использовалось поле касательного напряжения ветра τ (x, y, t), имитирующее кроме его пространственной неоднородности и сезонную изменчивость, для чего параметр S в формулах (1) задавался в виде функции от времени

 ,

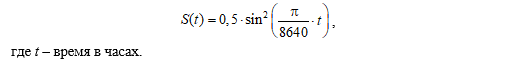Интенсивность ветрового воздействия регулировалась использованием в выражениях (1) различных амплитудных значений  . В эксперименте E2 они задавались равными 0,02 Н/м², что обеспечивало величину средней по площади моря и за год завихренности  . В эксперименте Е3 были заданы значения , равные 0,015 Н/м², при которых  . В обоих экспериментах α = 0,75.

Использование в экспериментах Е2 и Е3 ветра разной интенсивности объясняется наличием двух возможных режимов крупномасштабной циркуляции в Черном море. В работе [25] было продемонстрировано, что в зависимости от интенсивности ветрового воздействия в Черном море могут формироваться два различных режима крупномасштабной циркуляции. Первый режим устанавливается при превышении среднегодовой величины завихренности касательного напряжения ветра над всей акваторией моря   некоторого порогового значения Τ_пор. В данном режиме ОЧТ постоянно распространяется над материковым склоном, охватывая глубоководную область Черного моря по периметру. В случае, если   оказывается ниже порогового значения Τ_пор, формируется второй режим циркуляции. В этом режиме восточная ветвь ОЧТ периодически (один раз в 7–10 лет) отходит от береговой линии и перемещается в западном направлении, что вызывает смещение основного кольца циркуляции в западную половину Черного моря.

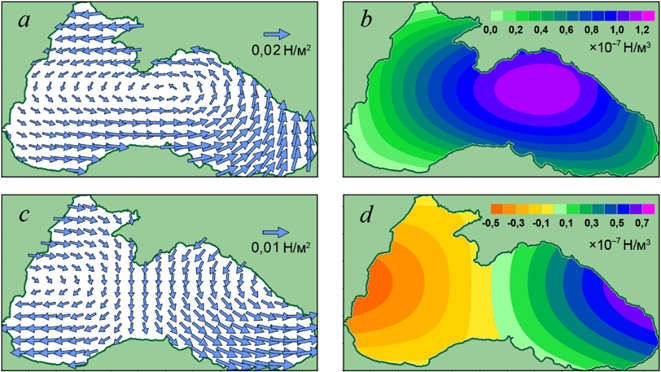
Р и с.  4. Поля τ и rot_Z τ в январе (a, b) и в июле (c, d) в эксперименте Е2

F i g.  4. Fields τ and rot_Z τ in experiment E2 in January (a, b) and July (c, d)

Поля τ и rot_Z τ для 1 января и 1 июля в эксперименте E2 показаны на рис. 4. Зимой над всем морем действует циклоническая завихренность τ с максимумом в восточной половине моря. Затем в течение первой половины года этот максимум смещается на восток, а над западной половиной моря устанавливается область с антициклонической завихренностью τ. Во второй половине года изменение τ и rot_Z τ происходит в противоположном направлении.

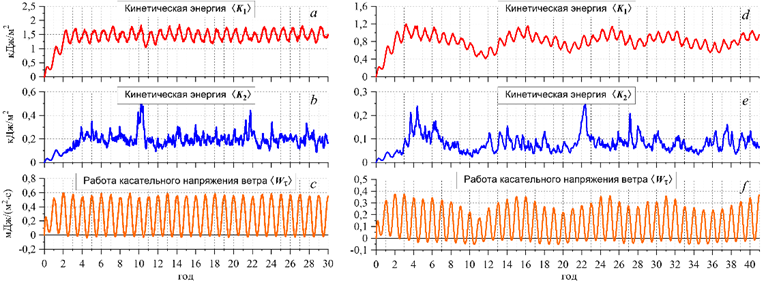
Временная изменчивость ⟨K₁⟩(t), ⟨K₂⟩(t), ⟨W_τ⟩(t) в эксперименте Е2 в виде графиков приведена на рис. 5, a, b, c. Видно, что сезонная изменчивость поля касательного напряжения ветра вызывает колебания притока ветровой энергии ⟨W_τ⟩ и интенсивности циркуляции в верхнем слое, индикатором которой служит ⟨K₁⟩. Сезонный ход ⟨K₁⟩ отстает от ⟨W_τ⟩ примерно на три месяца, что объясняется инерционностью динамической системы.

Р и с.  5. Графики кинетической энергии и работы касательного напряжения ветра в экспериментах Е2 (a, b, c) и Е3 (d, e, f)

F i g.  5. Graphs of kinetic energy and work of wind tangential stress in experiments E2 (a, b, c) and E3 (d, e, f)

Средняя по акватории моря кинетическая энергия течений в нижнем слое характеризуется сильной изменчивостью (рис. 5, b); при этом многие всплески ⟨K₂⟩ приходятся на моменты максимумов ⟨W_τ⟩. Однако однозначно связать ⟨K₂⟩ с сезонным ходом ⟨W_τ⟩ или ⟨K₁⟩ было бы необоснованно. Кроме того, сопоставляя графики временной изменчивости ⟨K₁⟩ и ⟨K₂⟩ (рис. 5, a, b), необходимо учитывать разницу в масштабах шкал и тот факт, что рассматриваются осредненные характеристики.

Динамику циркуляции в верхнем и нижнем слоях можно проследить по последовательным полям ζ (x, y) и М (x, y), приведенным на рис. 6. Изображения в двух горизонтальных верхних рядах соответствуют зимнему сезону, в двух нижних – летнему. На рисунках, которые отображают поля М, дополнительно нанесены изолинии ζ положения стрежня ОЧТ. Видно, что ОЧТ в верхнем слое моря более устойчиво в зимний период. Об этом можно судить по количеству и размеру меандров, которых в июле больше, чем в январе.

В нижнем слое в январе наблюдается усиление течений в центральной части глубоководной котловины моря по сравнению с июлем (рис. 6, b1 – b4, d1 – d4), что, вероятно, вызвано усилением экмановской накачки в зимний период. Другая причина может быть связана с перемещением над материковым подножием вдоль северо-восточного материкового склона более интенсивных вихревых образований, которые изначально образуются в юго-восточной части моря в районе Трабзона. По мере продвижения в сторону Крымского п-ова они постепенно ослабевают, но за ним снова активизируются, усиливая течения в западной части глубоководной котловины моря (рис. 6, b3, b4).

Р и с.  6. Мгновенные поля ζ (x, y) и М (x, y) в эксперименте Е2

F i g.  6. Instantaneous fields ζ (x, y) and М (x, y) in experiment E2

В летний период генерация, перемещение и трансформация вихревых образований вдоль северного материкового склона происходят аналогичным образом, но с меньшей интенсивностью (рис. 6, d3, d4).

При визуальном сравнении положения струи ОЧТ с вихревыми образованиями в нижнем слое (рис. 6, b1 – b4, d1 – d4) между ними обнаруживается согласованность. В большинстве случаев над циклоническими ВО струя ОЧТ направлена от берега в сторону моря, над антициклоническими – наоборот. Фазовые скорости перемещения меандров ОЧТ и ВО оказываются одинаковыми.

В эксперименте E3, как уже говорилось, использовалось поле касательного напряжения ветра, у которого средняя по акватории моря и за год завихренность была меньше порогового значения Τ_пор. В результате в модели возникали колебания интенсивности циркуляции с периодом 7–9 лет, которые хорошо видны на рис. 5, d. На графике ⟨K₂⟩ (рис. 5, e) подобные ⟨K₁⟩ колебания не наблюдаются, но имеются значительные амплитудные всплески, которые возникают чаще в зимний период. Причина колебаний ⟨K₁⟩ объясняется в работе [25] и заключается в изменении притока ветровой энергии ⟨W_τ⟩ вследствие перемещения струи ОЧТ от восточного берега на запад. Максимальные значения ⟨K₁⟩ наблюдаются в то время, когда ОЧТ распространяется по всему периметру глубоководной зоны моря, а минимумы ⟨K₁⟩ соответствуют периодам прохождения ОЧТ через центральную часть моря.

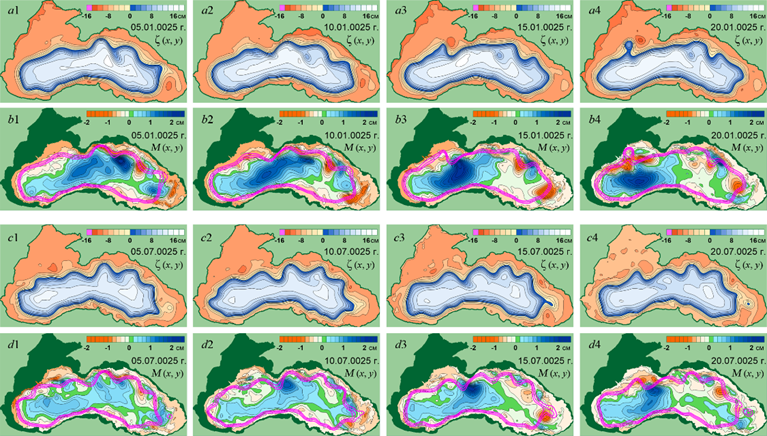
На рис. 7 показаны мгновенные поля ζ (x, y) и М (x, y), полученные в эксперименте Е3. Поля в двух горизонтальных верхних рядах характерны для периода, когда ⟨K₁⟩ достигает максимальных значений. В это время характер циркуляции в целом похож на наблюдаемый в эксперименте Е2 (рис. 6, d1 – d4).

В третьем и четвертом рядах рис. 7 приведены поля, которые формируются в периоды с минимальными значениями ⟨K₁⟩. В это время ОЧТ проходит через центр восточной части моря, соединяя турецкий берег с Новороссийском. При этом вследствие смещения ОЧТ из зоны материкового склона на востоке и северо-востоке моря циркуляция в нижнем слое ослабевает и прекращается генерация вихревых образований в юго-восточной части моря.

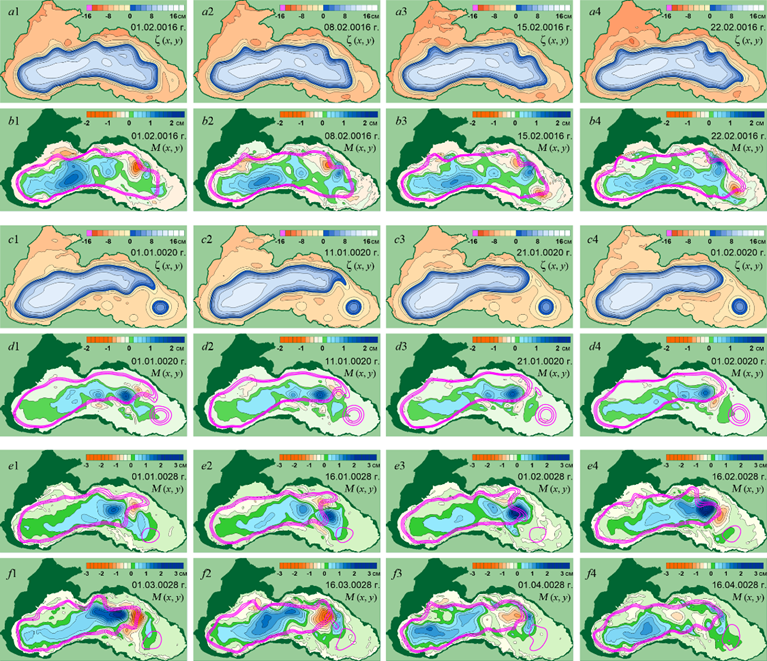
Р и с.  7. Мгновенные поля ζ (x, y) и М (x, y) в эксперименте Е3

F i g.  7. Instantaneous fields ζ (x, y) and М (x, y) in experiment E3

Поля ζ (x, y) и М (x, y), соответствующие резкому усилению ⟨K₂⟩ в начале февраля 28-го года от начала расчетов (рис. 5, e), представлены в двух нижних рядах на рис. 7. Данный всплеск ⟨K₂⟩ связан с образованием и интенсификацией мощного циклонического вихря над материковым подножием возле Кавказского побережья (рис. 7, e3, e4). После достижения максимума вихревое образование продолжило свое перемещение вдоль материкового подножия, что привело к усилению циклона в западной части глубоководной котловины моря.

Всплески ⟨K2⟩, вызванные интенсификацией вихревых образований, отмечались во всех рассматриваемых экспериментах, они характеризуют динамику нижнего слоя. Их проявление есть следствие гидродинамической неустойчивости крупномасштабных течений. Описанию механизмов генерации циркуляции в нижнем слое будет посвящена следующая работа.

Отметим, что полученные в двухслойной модели особенности пространственного распределения течений в нижнем слое моря достаточно хорошо согласуются с результатами моделирования, приведенными в работах [14, 15]. Однако в этих работах не проводится анализ динамики глубинных течений, не уделяется достаточное внимание объяснению причин возникновения вихревых образований в глубине моря.

Средние и «вихревые» течения

Для лучшего понимания динамических процессов в море использовался статистический метод, который заключается в разделении реальных (мгновенных) течений на средние и отклонения от этих средних (пульсации). Визуально пульсации течений чаще всего имеют вихревую структуру, поэтому их еще называют «вихревыми» течениями. Важным моментом при разделении течений на средние и «вихревые» является выбор периода осреднения, который определяется исходя из поставленных задач и конкретной динамики моря. Анализируя средние и «вихревые» течения, необходимо помнить, что такое разделение является условным, а в реальности существуют только суммарные течения.

Рассмотрим результаты применения статистического метода для эксперимента Е2. Течение в слоистой модели определяется как поток, равный произведению скорости течения на толщину слоя. В верхнем слое это , в нижнем . Тогда средние течения имеют вид , , а отклонения от средних (пульсации) Черта сверху означает осреднение по времени, верхний индекс «m» используем для обозначения средних течений, «p» – для пульсаций. Период осреднения задаем достаточно большой (не менее 20 лет), чтобы гарантированно исключить временную изменчивость средних течений.

На рис. 8 приведены поля средних и «вихревых» течений в верхнем слое (первый горизонтальный ряд) и нижнем слое (третий ряд) и соответствующие им поля ζ (второй ряд) и M (четвертый ряд). Средние поля  расположены в первом столбце, в столбцах со второго по четвертый расположены «вихревые» поля .

Видно, что в верхнем слое моря средние течения распространяются в области материкового склона, но не следуют изобатам. Направление потока соответствует изолиниям уровня моря, что является следствием геострофического баланса. Скорости средних течений в стрежне потока достигают 20 см/с, а ширина потока составляет 30–50 км. При выбранном периоде осреднения (20 лет) средние течения практически стационарны в верхнем и нижнем слоях.

Визуально пульсации течений в верхнем слое представляют собой чередующиеся циклонические и антициклонические вихри, перемещающиеся вдоль стрежня среднего ОЧТ в направлении против часовой стрелки (циклоническое вращение). В северной половине моря амплитуда этих вихрей значительно больше, чем в южной. Причина возникновения вихрей та же, что и причина образования меандров ОЧТ, – неустойчивость крупномасштабного течения.

Р и с.  8. Средние поля (a1), (b1), (c1),  (d1), мгновенные поля (a2 – a4), (b2 – b4), (c2 – c4), (d2 – d4) в эксперименте Е2

F i g.  8. Мean fields  (a1),  (b1),  (c1) and (d1), and instantaneous fields  (a2 – a4),  (b2 – b4),  (c2 – c4), and  (d2 – d4) in experiment E2

В нижнем слое моря на средние течения большое влияние оказывает рельеф дна, в результате чего линии тока средних течений, в качестве которых выступают изолинии , оказываются близки к изобатам.

Пульсационная («вихревая») составляющая глубинных течений также представляет собой чередующиеся мезомасштабные вихревые образования, распространяющиеся в циклоническом направлении над материковым склоном и материковым подножием. Вероятными причинами образования данных вихрей являются неустойчивость ОЧТ, топографический и планетарный β-эффект.

Визуально поля «вихревых» и мгновенных течений в нижнем слое имеют значительное сходство, что указывает на большой вклад вихревой составляющей течений в суммарный поток. Для подтверждения этого умозаключения рассчитаем среднюю по времени кинетическую энергию средних  и «вихревых»  течений в слоях:

После осреднения по площади получим следующие значения:

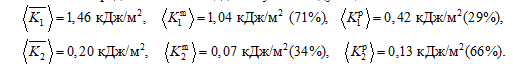
Таким образом, в верхнем слое бóльшая часть энергии содержится в средних течениях (71 %), меньшая – в «вихревых» (29 %); в нижнем слое, наоборот, на «вихревые» течения приходится 66 % кинетической энергии, на средние – только 34 %.

Интересно отметить, что в результате разделения течений на средние и «вихревые» в верхнем слое удается выделить вихревые образования на месте меандров ОЧТ. В нижнем слое, наоборот, процедура осреднения позволяет выявить наличие средних течений, близких к изобатам, которые визуально не видны в мгновенных полях.

Параметры волновых колебаний глубинных течений

Для определения дисперсионных характеристик волновых процессов в поле глубинных течений были построены диаграммы временной изменчивости характеристик течений вдоль траектории распространения волн.

Поскольку градиентно-вихревые волны представляют собой колебания вектора течений в горизонтальной плоскости, было бы логично использовать для построения диаграмм поперечную составляющую скорости течений. Но поскольку для крупномасштабных и мезомасштабных динамических процессов выполняется геострофический баланс, то в качестве исходных данных были использованы поля М (x, y, t), полученные в эксперименте E2.

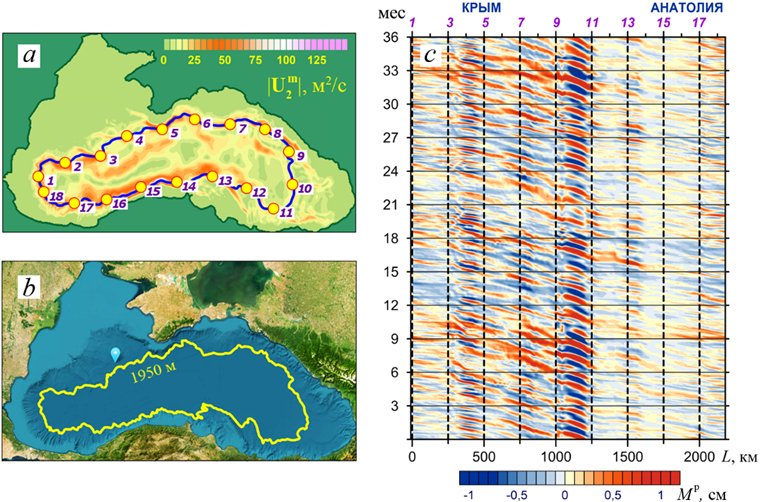
За отсчетный уровень был выбран стрежень среднего течения – линия тока с максимальными значениями потока (рис. 9, a). В силу геострофичности средних течений в качестве линии тока использовалась соответствующая стрежню потока нулевая изолиния  (рис. 8, d1), которая оказалась близка к изобате H = 1950 м (рис. 9, b). Необходимо заметить, что вследствие влияния рельефа дна в поле средних потоков оказалось несколько стрежней.

Для того, чтобы в дальнейшем было возможно сопоставить временную диаграмму с картой Черного моря, на ней через равные расстояния были отмечены контрольные точки (рис. 9, a).

Диаграмма временной изменчивости с дискретностью 1 сут функции  вдоль нулевой изолинии  для трехлетнего временного интервала (23-й – 25-й годы) приведена на рис. 9, с. Вертикальные штриховые линии, пронумерованные над верхней осью, соответствуют контрольным точкам, показанным на рис. 9, а.

Р и с.  9. Модуль среднего потока в нижнем слое  (a), изобата H = 1950 м (b), временная диаграмма M ^p вдоль изолинии M ^m (c)

F i g.  9. Modulus of average flow in the lower layer  (a), isobath H = 1950 m (b), and time diagram M ^p along isobaths M ^m (c)

На диаграмме хорошо видно перемещение знакопеременных пульсаций , соответствующих прохождению волн вдоль выбранной траектории в направлении против часовой стрелки. По наклону линий, соединяющих одинаковые фазы колебаний, можно судить о фазовой скорости волн, которая отличается на различных отрезках траектории. Наиболее быстро волны движутся между точками 18–11, расположенными в южной части маршрута.

Согласно диаграмме, между точками 11–9 на востоке моря происходит интенсификация волновых процессов. Ранее уже говорилось, что в этом районе происходит генерация топографических волн (рис. 6, 8). Также заметно усиление амплитуды колебаний между точками 5 и 3 на отрезке траектории, который начинается южнее Крымского п-ова и простирается на запад.

Второй этап определения дисперсионных характеристик волновых колебаний заключался в использовании диаграммы (рис. 9, с) для построения двухмерного волнового спектра с помощью алгоритма быстрого преобразования Фурье (БПФ). Временная диаграмма представляет собой массив данных из 1080 реализаций суточных значений функции M вдоль траектории L с дискретностью 2 км.

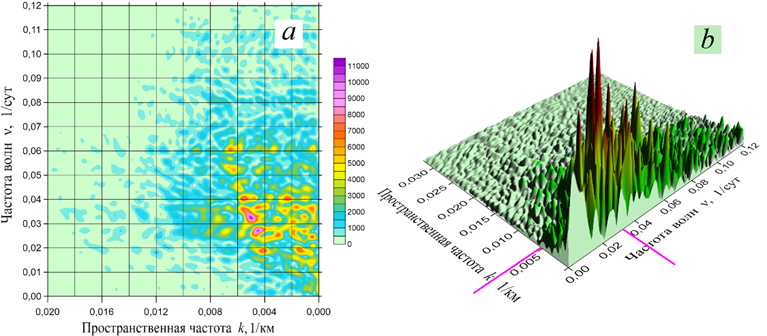
Построенный двухмерный (по частоте и пространственной частоте) спектр S = f (ν, k) показан на рис. 10 в форматах 2D и, для наглядности, 3D.

Согласно рис. 10, волновые процессы в поле глубинных течений попадают в диапазоны 0,01–0,06 1/сут по частоте и 0,005–0,08 1/км – по пространственной частоте, что соответствует волнам с периодами 17–100 сут и длинами 12–200 км. Такие волны принято считать длинными, поскольку наименьшая в интервале длина волны в несколько раз превосходит глубину моря.

Р и с.  10. Двухмерный спектр волновых колебаний в поле глубинных течений в форматах 2D (a), 3D (b)

F i g.  10. Two-dimensional spectrum of wave oscillations in the field of deep currents in 2D (a) and 3D (b) formats

Большой разброс дисперсионных характеристик волн можно объяснить изменяющимся наклоном дна вдоль траектории их перемещения и наличием различных механизмов генерации этих волн. Тем не менее полученные дисперсионные характеристики вместе с внешними проявлениями волн (вихревой характер, направление движения, зависимость от рельефа) соответствуют диагностируемым ранее волнам, захваченным материковым склоном с учетом планетарного β-эффекта.

В полученном спектре наибольший вес приходится на волну с частотой ν = 0,033 1/сут и пространственной частотой k = 0,0051 1/км, что соответствует волне с длиной λ = 196 км и периодом T = 30 сут, которая движется вдоль выбранной траектории (рис. 9, a) с фазовой скоростью C_ф = 0,078 м/с. Подобные дисперсионные характеристики волн ранее встречались в работе [26] и относились к меандрам ОЧТ, наблюдаемым в районе Геленджика.

Нужно отметить, что рассмотренный спектр (рис. 10) отражает характеристики волн только вдоль одной траектории. Очевидно, что для других траекторий результаты спектрального анализа могут отличаться. Различные дисперсионные характеристики волн также могут быть получены для разных участков одного маршрута.

Заключение

Подводя итоги проделанной работы и учитывая результаты анализа проведенных численных экспериментов, можно предположить, что глубинная циркуляция в Черном море представляет собой комбинацию знакопеременных вихревых образований и средних течений, направленных примерно вдоль изобат. Вихревые образования распространяются по периметру глубоководной части моря в циклоническом направлении в виде длинных волн, дисперсионные характеристики которых соответствуют волнам, захваченным наклонным дном, в качестве которого выступают материковый склон и материковое подножие.

Главным элементом глубинной циркуляции следует считать вихревые образования, поскольку они содержат бо́льшую часть (2/3) кинетической энергии глубинных течений. Для сравнения, в верхнем слое «вихревые» течения обеспечивают только 1/3 часть кинетической энергии.

Генеральное направление глубинной циркуляции циклоническое – против часовой стрелки. В этом направлении распространяются фазы захваченных волн и переносится вода средними течениями. Фазовые скорости длинных волн больше, чем скорости средних течений.

Можно предположить два возможных источника генерации глубинных течений в Черном море. Одним из них является экмановская накачка – ветровой механизм генерации геострофических течений. В двухслойной модели экмановская накачка проявляется в подъеме поверхности раздела слоев, что приводит к возникновению течений в нижнем (глубоководном) слое. Другой вероятный источник – неустойчивость ОЧТ, вследствие которой могут генерироваться вихревые возмущения как в верхнем, так и в нижнем слое моря.

Согласно полученным результатам, в Черном море выделяются два района, в которых происходит образование и/или усиление длинных волн. Один такой район расположен на востоке моря возле Трабзона, другой – к юго-западу от Крымского п-ова.

В ходе исследования глубинной циркуляции возник ряд вопросов, которые не были в достаточной мере освещены в настоящей работе, но имеют несомненный интерес с научной точки зрения. Один вопрос относится к пространственному распределению дисперсионных характеристик длинных волн. Два других связаны с механизмами генерации глубинных течений и оценкой степени влияния на образование вихревых волн в глубине моря факторов неустойчивости ОЧТ, планетарного и топографического β-эффекта. Данные вопросы будут рассмотрены в следующих работах.

Еще один вопрос касается соответствия представленной здесь схемы течений в нижнем слое реальной циркуляции в глубине Черного моря. Он может быть решен только с помощью проведения соответствующих натурных экспериментов.

1. Иванов В. А., Белокопытов В. Н. Океанография Черного моря. Севастополь : МГИ НАН Украины, 2011. 212 c.

2. Коновалов С. К., Видничук А. В., Орехова Н. А. Пространственно-временные характерис-тики гидрохимической структуры вод глубоководной части Черного моря // Система Черного моря. / [А. П. Лисицын, Н. В. Короновский, Ал. А. Шрейдер и др. ; ответ-ственный редактор: А. П. Лисицын]. М. : Научный мир, 2018. C. 106–118. EDN IPZOJH. https://doi.org/10.29006/978-5-91522-473-4.2018.106

3. Статистические характеристики глубинных течений в Черном море по данным инстру-ментальных измерений / В. А. Иванов [и др.] // Фундаментальная и прикладная гидрофизи-ка. 2019. Т. 12, № 4. С. 49–58. EDN JCGBIR. https://doi.org/10.7868/S2073667319040063

4. Маркова Н. В., Багаев А. В. Оценка скоростей глубоководных течений в Черном море по данным дрейфующих буев-профилемеров Argo // Морской гидрофизический журнал. 2016. № 3. С. 26–39. EDN WNAFSV. https://doi.org/10.22449/0233-7584-2016-3-26-39

5. Энергетический спектр скорости течения в глубокой части Чёрного моря / А. А. Клю-виткин [и др.] // Доклады Академии наук. 2019. Т. 488, № 5. C. 550–554. EDN RUPYJT. https://doi.org/10.31857/S0869-56524885550-554

6. Построение поля течений в Черном море на основе вихреразрешающей модели с асси-миляцией климатических полей температуры и солености / С. Г. Демышев [и др.] // Экологическая безопасность прибрежной и шельфовой зон и комплексное исполь-зование ресурсов шельфа. 2007. № 15. C. 215–226. EDN YMTPYD.

7. Numerical model of the circulation of the Black Sea and the Sea of Azov / V. B. Zalesny [et al.] // Russian Journal of Numerical Analysis and Mathematical Modelling. 2012. Vol. 27, iss. 1. P. 95–112. https://doi.org/10.1515/rnam-2012-0006

8. Залесный В. Б., Гусев А. В., Мошонкин С. Н. Численная модель гидродинамики Черного и Азовского морей с вариационной инициализацией температуры и солености // Известия РАН. Физика атмосферы и океана. 2013. Т. 49, № 6. С. 699–716. EDN RFWNGV. https://doi.org/10.7868/S000235151306014X

9. Коротенко К. А. Моделирование мезомасштабной циркуляции Черного моря // Океанология. 2015. Т. 55, № 6. С. 909–915. EDN UVEPDV. https://doi.org/10.7868/S0030157415060076

10. Дорофеев В. Л., Сухих Л. И. Анализ изменчивости гидрофизических полей Черного моря в период 1993–2012 годов на основе результатов выполненного реанализа // Морской гидро-физический журнал. 2016. № 1 (187). С. 33–48. EDN VTPCZH. https://doi.org/10.22449/0233-7584-2016-1-33-48

11. Коршенко Е. А., Дианский Н. А., Фомин В. В. Воспроизведение глубоководной циркуля-ции Черного моря с помощью модели INMOM и сопоставление результатов с данными буев ARGO // Морской гидрофизический журнал. 2019. Т. 35, № 3 (207). С. 220–232. EDN WDPFVK. https://doi.org/10.22449/0233-7584-2019-3-220-232

12. Rim current and coastal eddy mechanisms in an eddy-resolving Black Sea general circulation model / J. V. Staneva [et al.] // Journal of Marine Systems. 2001. Vol. 31, iss. 1–3. P. 137–157. https://doi.org/10.1016/S0924-7963(01)00050-1

13. Gunduz M., Özsoy E., Hordoir R. A model of Black Sea circulation with strait exchange (2008–2018) // Geoscientific Model Development. 2020. Vol. 13, iss. 1. P. 121–138. https://doi.org/10.5194/gmd-13-121-2020

14. Численные эксперименты по реконструкции глубинных течений в Черном море / С. Г. Демышев [и др.] // Морской гидрофизический журнал. 2016. № 2. С. 38–52. EDN VWXGZH. https://doi.org/10.22449/0233-7584-2016-2-38-52

15. Дымова О. А., Миклашевская Н. А., Маркова Н. В. Особенности глубоководной циркуля-ции Черного моря летом 2013 // Экологическая безопасность прибрежной и шельфовой зон моря. 2019. № 1. С. 40–47. EDN ZCJLSX. https://doi.org/10.22449/2413-5577-2019-1-40-47

16. Маркова Н. В., Дымова О. А. Условия формирования глубоководных противотечений в северо-восточной части Черного моря // Известия РАН. Механика жидкости и газа. 2023. № 5. С. 25–36. EDN TSHOAY. https://doi.org/10.31857/S1024708423600057

17. Двухслойная вихреразрешающая модель ветровых течений в Черном море / А. А. Павлу-шин [и др.] // Морской гидрофизический журнал. 2015. № 5. С. 3–22. EDN VHEWTL. https://doi.org/0.22449/0233-7584-2015-5-3-22

18. Павлушин А. А., Шапиро Н. Б., Михайлова Э. Н. Роль рельефа дна и β-эффекта в динамике Черного моря // Морской гидрофизический журнал. 2017. № 6. С. 27–39. EDN QHQKPF. https://doi.org/10.22449/0233-7584-2017-6-27-39

19. Михайлова Э. Н., Шапиро Н. Б. Трехмерная негидростатическая модель субмаринной разгрузки в прибрежной зоне моря // Морской гидрофизический журнал. 2014. № 4. С. 28–50. EDN TEVDNJ.

20. Ефимов В. В., Юровский А. В. Формирование завихренности поля скорости ветра в ат-мосфере над Черным морем // Морской гидрофизический журнал. 2017. № 6. С. 3–12. EDN YLLPWD. https://doi.org/10.22449/0233-7584-2017-6-3-12

21. Павлушин А. А., Шапиро Н. Б., Михайлова Э. Н. Влияние сезонной изменчивости завих-ренности ветра на структуру циркуляции в Черном море // Морской гидрофизический журнал. 2018. Т. 34, № 5. С. 373–388. EDN VLBKLC. https://doihttps://doi.org/10.22449/0233-7584-2018-5-373-388

22. Бассейновая циркуляция и мезомасштабная динамика Черного моря под ветровым воз-действием / А. Г. Зацепин [и др.] // Современные проблемы динамики океана и атмосферы: сб. статей, посвященный 100-летию со дня рождения проф. П. С. Линейкина / Под ред. А. В. Фролова, Ю. Д. Реснянского. М. : Триада ЛТД, 2010. С. 347–368. EDN TVXEMZ.

23. Белоненко Т. В., Захарчук Е. А., Фукс В. Р. Градиентно-вихревые волны в океане. СПб. : Изд-во С.-Петерб. ун-та, 2004. 212 с.

24. Жмур В. В., Новоселова Е. В., Белоненко Т. В. Потенциальная завихренность в океане: подходы Эртеля и Россби с оценками для Лофотенского вихря // Известия РАН. Физика атмосферы и океана. 2021. Т. 57, № 6. С. 721–732. EDN SRKASA. https://doi.org/10.31857/S0002351521050151

25. Павлушин А. А. Автоколебания интенсивности крупномасштабной циркуляции в Черном море // Морской гидрофизический журнал. 2022. Т. 38, № 6. С. 605–619. EDN UFLDYX. https://doi.org/10.22449/0233-7584-2022-6-605-619

26. О влиянии изменчивости течения в глубоководной зоне Черного моря на динамику вод узкого северокавказского шельфа / А. Г. Зацепин [и др.] // Морской гидрофизический журнал. 2016. № 3. С. 16–25. EDN WNAFSL. https://doihttps://doi.org/10.22449/0233-7584-2016-3-16-25