Россия
УДК 532.59 Волновое движение
Цель. Определены частоты резонансных колебаний уровня водной поверхности Азовского моря. Методы и результаты. Вычислительные эксперименты проводились на математической моде-ли, основанной на системе уравнений длинных волн в однородной жидкости. В качестве внешней силы выступал ветер переменного направления или переменной силы, а также колебание атмо-сферного давления. Задача решалась конечно-разностными методами с использованием неявных разностных схем. Получены значения длины периодов, при которых наступает резонансный эф-фект. Значения частоты колебаний определялись с помощью вычисления полной энергии осцил-ляций как суммы потенциальной и кинетической энергии. Установлено совпадение значений резонансной частоты (или периодов) колебаний уровня воды в условиях переменной ветровой нагрузки и изменяющегося атмосферного воздействия. Установлено, что устойчивые резонанс-ные колебания могут наступать уже после четырех – семи периодов действия внешней периоди-ческой силы, после чего колебательные движения стабилизируются. Выводы. Используемая математическая модель позволяет проводить вычислительные экспери-менты для исследования процесса образования резонансных колебаний уровня воды в Азовском море. Результаты исследования адекватно описывают периодическое слабое внешнее воздей-ствие на водную поверхность Азовского моря. Результаты расчетов резонансных частот согла-суются с результатами, полученными другими авторами.
уравнения мелкой воды, резонанс, резонансные колебания, сейша, вычислительный эксперимент
Введение
Колебательные движения воды в замкнутых или полузамкнутых водоемах могут возникать при довольно слабом физическом воздействии на водную поверхность, если это воздействие попадает в резонанс с собственными колебаниями водоема. К подобным водоемам вполне относится Азовское море. Приводя в движение всю массу воды Азовского моря, созданные колебания влияют на его гидрологический режим. Во многих работах такие резонансные колебания отождествляются с сейшами и моделируются путем приложения возмущающей силы к поверхности водоема с последующим анализом свободных колебаний поверхности после прекращения воздействия. Возмущения могут задаваться как ветровым воздействием, так и колебаниями водной поверхности, индуцированными изменениями атмосферного давления. Для определения сейш проводится расчет вынужденных колебаний с целью определения резонанса с собственными колебаниями водоема.
При совпадении внешних воздействий, даже малой амплитуды, с собственными частотами колебаний водоема, могут возникать сейши, представляющие значительные риски для антропогенной инфраструктуры и экосистем В работе [1] проведен анализ многолетней динамики и повторяемости опасных и неблагоприятных колебаний уровня Азовского моря, приводящих к катастрофическим подъемам уровня воды, разрушению берегов, затоплению кос Должанской, Ейской, Чумбурской, Очаковской и разрушению прибрежных строений.
Методом математического моделирования в [2] исследовано влияние неоднородных перемещающихся полей атмосферного давления на течения, свободные и вынужденные колебания уровня Азовского моря, вызываемые действием постоянного ветра, а также барическими возмущениями. Исследование свободных и вынужденных колебаний в Азовском море выполнено методом математического моделирования с помощью трехмерной сигма-координатной модели POM (Princeton Ocean Model).
В работе [3] для Азовского моря в качестве вынуждающей силы задаются колебания уровня воды (нагона) у Керченского пролива. Резонансная частота устанавливается по максимальному значению полной энергии, наблюдаемому при изменении частоты возбуждающих колебаний. Общая энергия определялась как сумма кинетической и потенциальной энергии.
В работе [4] для Балаклавской бухты задаются колебания уровня воды и скорости течения. В начальный момент времени жидкость находится в состоянии покоя. Затем на открытой границе бассейна начинает действовать периодическое возмущение. Ставится задача определить периоды собственных колебаний бассейна, изучить структуру полей уровня и течений при полученных значениях периодов.
Целью работы [5] является нахождение в линейном приближении аналитического решения задачи о сейшах для прямоугольного бассейна постоянной глубины, которое позволяет рассчитать периоды мод сейшевых колебаний, отклонения свободной поверхности и скорости волновых течений. На основе полученного решения исследуются сейшевые и сейшеобразные колебания. Решение ищется в виде периодических по времени функций. Расчеты были проведены для прямоугольного бассейна длиной 450 км, шириной 250 км, глубиной 10 м, являющегося приближенной моделью Азовского моря, имеющей его характерные размеры.
В работе [6] свободные колебания уровня моря моделировались гидродинамически с учетом массовых сил, включая силу Кориолиса и донное трение. В качестве исходной системы уравнений использовалась нелинейная система уравнений мелкой воды. Над морем с нулевыми начальными значениями уровня и течений задавался однородный и постоянный ветер разных направлений. Через 10 ч ветер отключался и исследовались свободные колебания уровня.
Подобный подход к изучению свободных колебаний уровня воды в Азовском море, возникающих после прекращения действия постоянного ветра, представлен в [7]. В данной работе используется сигма-координатная модель, с помощью которой определяются характеристики сейшеобразных колебаний.
В работе [8] скорость и время движения барического поля выбраны в предположении, что волны генерируются с максимальными амплитудами. Это возможно, когда период вынуждающей силы приближается к периоду собственных колебаний бассейна. Время перемещения фронта над всей акваторией моря задается равным времени наибольшего подъема уровня Азовского моря, который происходит в течение половины периода старшей моды свободных колебаний.
На основании анализа результатов численного моделирования в работе [9] исследованы сейшеобразные колебания уровня Азовского моря в поле возмущений атмосферного давления. При этом период возмущающих давлений равен периоду собственных колебаний жидкости в бассейне.
Целью данной работы является численное исследование возникновения резонансных колебаний водной поверхности Азовского моря в результате слабых периодических внешних воздействий. Такими вынуждающими силами может быть слабый ветер переменных направлений или переменной силы, а также меняющееся с определенным периодом атмосферное давление. Вычислительные эксперименты проводились на математической модели, созданной в Южном научном центре РАН [10].
Материалы и методы
Расчеты колебаний уровня в Азовском море основываются на решении системы уравнений для длинных волн в однородной несжимаемой жидкости в поле силы Кориолиса с учетом атмосферного давления, как это сделано в работе [11]:
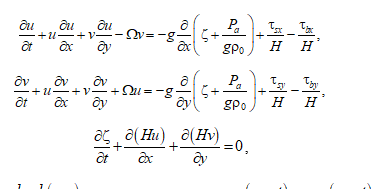

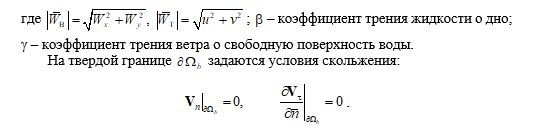 .
.
Задача решается конечно-разностными методами на равномерной сетке с использованием неявных разностных схем. Конвективные члены уравнения количества движения аппроксимировались разностями против потока. Перепад уровня воды определяется из соответствующего разностного аналога. Шаг сетки составлял ∆x = 660 м и ∆y = 685 м с числом узлов 524 ×354. После индексации ячеек в расчетной области число неизвестных по каждой переменной стало примерно 83 000. Аналитическая оценка допустимого шага по времени в используемых разностных схемах не проводилась, но численные расчеты показали устойчивость счета при Δt < 120. Программа написана на языке FORTRAN, численная реализация модели осуществлялась на высокопроизводительных вычислительных системах в среде MPI с использованием пакета параллельных подпрограмм Aztec.
Резонансная частота собственных и вынужденных колебаний определялась с помощью вычисления средней за период полной энергии как суммы кинетической и потенциальной
энергии. Расчет полной энергии проводился по методике [3]:
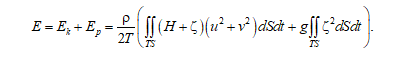
Здесь r – плотность морской воды (принятая в модели постоянной и равной 1000 кг/м3); Т – период колебаний; S – площадь области расчета. При построении графиков рассматривался натуральный логарифм полной энергии .
Результаты и обсуждение
Исследован диапазон изменения периода вынужденных колебаний от 2 до 30 ч. Резонанс наблюдался при тех частотах, при которых полная энергия имела локальный максимум. Рассмотрены следующие основные сценарии возникновения резонансных колебаний уровня воды в Азовском море:
- направление ветра меняется с СВ на ЮЗ при неизменной скорости 2 м/с;
- действие восточного ветра скоростью 2 м/с чередуется со штилем;
- атмосферное давление на восточной и западной границах Азовского моря поочередно колеблется от 750 до 770 мм рт. ст.
Кроме этих основных сценариев, были рассмотрены направления ветра СЗ – ЮВ и С – Ю.
Шаг изменения периода вынужденных колебаний (изменения ветровой нагрузки или давления) равнялся 0,2 ч. Для получения более устойчивой картины резонанса для каждого периода внешнее воздействие изменялось 15 раз.
Наиболее сильно выделяющийся локальный максимум энергии наблюдался несколько раз – для значений периода 6,4; 15,2; 19,2 и 26 ч (рис. 1). Это наблюдалось и при ветрах СВ – ЮЗ, и при смене восточного ветра на штиль, и при колебаниях атмосферного давления. Кроме того, можно выделить еще несколько небольших всплесков энергии. Данные частоты наблюдались для всех румбов ветра, что соответствовало как продольным, так и поперечным воздействиям на поверхность моря. Отличалась только величина полной энергии.
Была рассмотрена ситуация, когда ветер скоростью 2 м/с менял направление с ЮВ на СЗ, а также чередовал восточное направление со штилем. Наиболее выраженные локальные максимумы энергии наблюдались для значений периода 6,4; 15,2 и 26 ч, что не противоречит результатам, полученным другими авторами. Так, в работе [14] указано, что в колебаниях уровня Азовского моря можно выделить три моды колебаний – 23; 14,5 и 6–8 ч. Более высокие моды колебаний менее значительны и не характерны для всего моря. Колебания с периодом 23,7 ч указаны в работе [3], но автор их относит к двухузловой сейше.
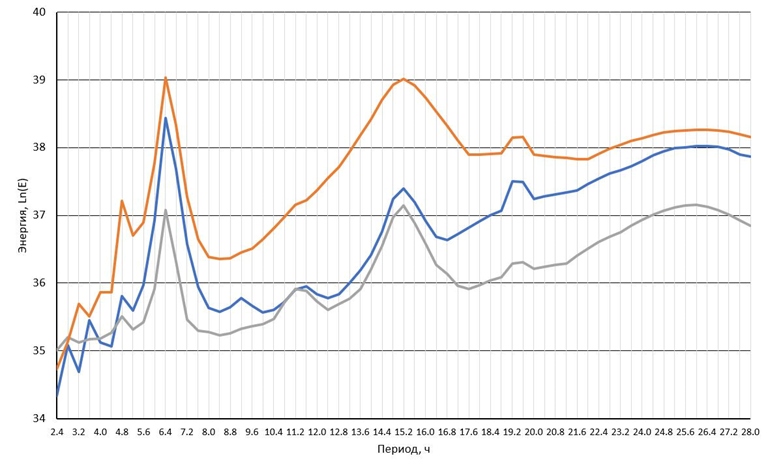
Р и с. 1. Зависимость логарифма энергии от частоты ветрового воздействия при смене направления постоянного ветра скоростью 2 м/с с СВ на ЮЗ (синяя кривая) (а); при чередующемся воздействии восточного ветра скоростью 2 м/с и штиля (серая кривая) (b); при колебаниях атмосферного давления на восточной и западной границах Азовского моря в диапазоне 750–770 мм рт. ст. (оранжевая кривая) (с)
F i g. 1. Dependence of the energy logarithm on wind impact frequency at: changing the direction of constant wind (speed 2 m/s) from NE to SW (blue curve) (a), alternating action of east wind (speed 2 m/s) and calm (gray curve) (b), and fluctuations in atmospheric pressure at the eastern and western boundaries of the Azov Sea in the range 750–770 mm Hg (orange curve) (c)
На приведенных ниже рисунках показано распределение уровней водной поверхности моря при максимальном значении полной энергии.
При периоде колебаний ветра 26 ч движение воды в Азовском море имеет циркуляционный характер с образованием нескольких зон циркуляции как в самом Азовском море, так и в Таганрогском заливе. На рис. 2 показано распределение уровня водной поверхности и линии тока с максимумом в Таганрогском заливе (0,85 м) и минимумом у Арабатской Стрелки (−0,15 м), которые сменяются на минимум в Таганрогском заливе (−0,74 м) и максимум у Арабатской Стрелки (0,31 м). Узловая линия сейши проходит примерно от основания Должанской косы к Бердянску. Подобный результат описан в работе [9].
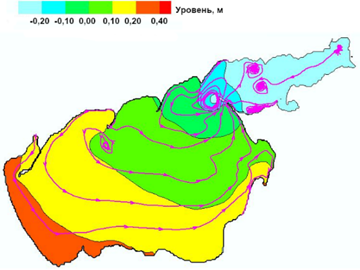
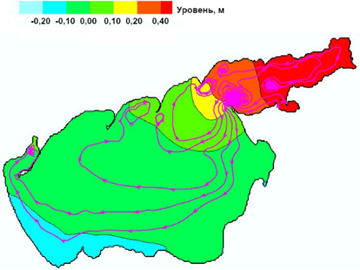
2. Резонансные колебания при смене ветром скоростью 2 м/с направления с СВ на ЮЗ: а – в конце периода Т = 26.0 ч; b – в конце полупериода Т/2 = 13,0 ч
F i g. 2. Resonant oscillations at changing wind (speed 2 m/s) direction from NE to SW at the end of: а – period T = 26.0 h, and b – semi-period T/2 = 13.0 h
Наблюдения с метеостанций и гидропостов за колебаниями уровня воды показали, что чаще всего действуют колебания с периодом примерно 24 ч. Такие колебания уровня воды с периодом 23–25 ч описаны в работах [5, 7]. В работе [7] указано, что доминирующие продольные собственные колебания первой моды уровня Азовского моря имеют период, приблизительно равный 24 ч. Структура этой моды такова, что одна ее вершина находится в Таганрогском заливе, а противоположная – вблизи Геническа. Такая ситуация очень близка к полученной нами картине, представленной на рис. 2.
При периоде колебаний ветра 19,2 ч движение воды в Азовском море также имеет циркуляционный характер с образованием нескольких зон циркуляции, как и в случае с периодом 26 ч. Однако амплитуда колебаний в этом случае меньше и равна 0,25 м для максимума и −0,45 м для минимума.
При колебаниях ветра с периодом 15,2 ч движение воды в Азовском море имеет в основном поступательный характер (рис. 3), прослеживается двухуз-ловая сейша. В этом случае наблюдаются два максимума уровней – в Таганрогском заливе (0,39 м) и Утлюкском лимане (0,42 м) – и минимум в районе Приморско-Ахтарска (−0,44 м), которые сменяются соответственно на максимум в районе Приморско-Ахтарска и два минимума в Таганрогском заливе и Утлюкском лимане. Одна узловая линия соединяет район Керченского пролива с Бердянским заливом. Вторая узловая линия соединяет район Ейска с Белосарайской косой.
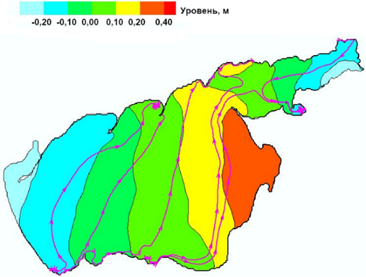
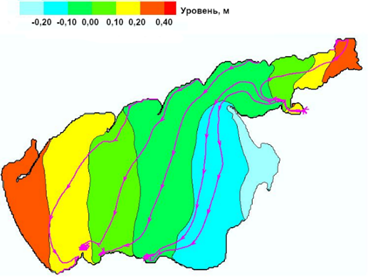
Р и с. 3. Резонансные колебания при смене ветром скоростью 2 м/с направления с СВ на ЮЗ: а – в конце периода Т = 15,2 ч; b – в конце полупериода Т/2 = 7,6 ч
F i g. 3. Resonant oscillations at changing wind (speed 2 m/s) direction from NE to SW at the end of: а – period T = 15.2 h, and b – semi-period T/2 = 7.6 h
При периоде ветровых колебаний 6,4 ч (рис. 4) основные колебания уровня воды происходят в самом Азовском море. Максимальный уровень регистрируется в районе Приморско-Ахтарска и Обиточном заливе (0,85–1,0 м), минимальный – в районе устья Кубани и у Арабатской Стрелки (−0,55 м). Через половину периода (3,2 ч) пространственное распределение экстремумов уровня инвертируется. Одна узловая линия проходит через центр Азовского моря из района Приморско-Ахтарска к Бирючему Острову. Остальные две узловые линии находятся на границе Таганрогского залива и в его центральной части.
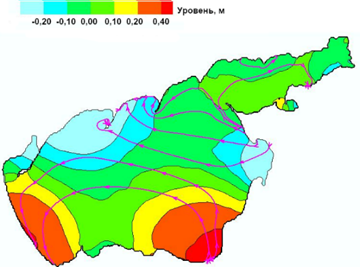
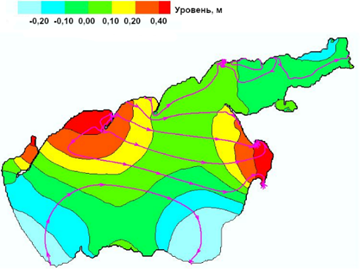
Р и с. 4. Резонансные колебания при смене ветром скоростью 2 м/с направления с СВ на ЮЗ: а – в конце периода Т = 6,4 ч; b – в конце полупериода Т/2 = 3,2 ч
F i g. 4. Resonant oscillations at changing wind (speed 2 m/s) direction from NE to SW at the end of: а – period T = 6.4 h, and b – semi-period T/2 = 3.2 h
Дальнейшее исследование колебаний при пиковых частотах показало, что при частоте колебаний ветра с периодом 26 ч резкое увеличение полной энергии начинает наблюдаться уже в четвертом периоде действия вынуждающего воздействия. Различие в значениях полной энергии для последующих периодов не превышает 1 %. Для колебаний с периодом 15,2 ч резкое увеличение полной энергии начинает наблюдаться в шестом периоде, а для колебаний с периодом 6,4 ч – в седьмом периоде.
При дальнейшем внешнем колебательном воздействии на поверхность моря с периодами 6,4; 15,2; 26, а также 19,2 ч значение полной энергии продолжает устойчиво увеличиваться, что говорит о возможном наступлении резонанса (рис. 5). Заметим, что частота при периоде 19,2 ч ранее не была рассмотрена как резонансная. Для частот с периодом колебаний 2,8; 4,8 ч дальнейшее внешнее воздействие приводит к уменьшению полной энергии, что говорит о затухании колебаний.
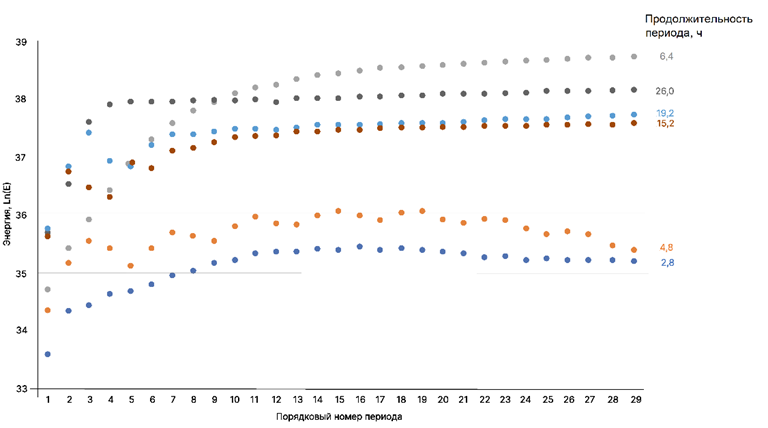
Р и с. 5. Полная энергия для пиковых значений периодов (ч) колебаний при ветровом воздействии на поверхность Азовского моря
F i g. 5. Total energy for peak values of oscillation periods (h) under wind impact on the Azov Sea surface
В случае, когда происходит чередование действия ветра со штилем, картины распределения уровней поверхности воды в Азовском море подобны наблюдавшимся в предыдущей ситуации.
Генерация вынужденных колебаний уровня воды в Азовском море проводилась также с помощью колебаний атмосферного давления. Предполагалось, что ветровая нагрузка полностью отсутствует. На западной (Арабатская Стрел-ка) и восточной (устья рукавов Дона) границах моря задавались разные значения давления, связанные линейной зависимостью. Атмосферное давление задавалось равным 750 мм рт. ст. на одном конце Азовского моря и 770 мм рт. ст. на другом конце. Пиковые значения полной энергии, предсказуемо, соответствуют частотам изменения давления, совпадающим с частотами колебаний ветровой нагрузки (см. рис. 1): с периодами 6,4; 15,2; 19,2 и 26 ч. Отличительной особенностью является отсутствие всплесков полной энергии для периодов 9,2 и 11,6 ч, а также аномальное поведении энергии на периодах, меньших 6,4 ч.
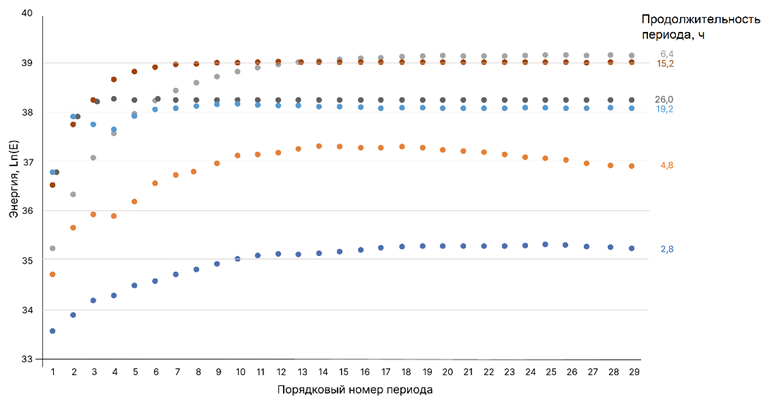
Р и с. 6. Полная энергия для пиковых значений периодов (ч) колебаний при воздействии атмосферным давлением на поверхность Азовского моря
F i g. 6. Total energy for peak values of oscillation periods (h) under the influence of atmospheric pressure on the Azov Sea surface
При дальнейшем воздействии атмосферного давления на поверхность моря с пиковыми частотами для периодов 6,4; 15,2; 19,2; и 26 ч значение полной энергии стабилизируется, а для периодов 2,8; 4,8 ч полная энергия уменьшается (рис. 6). Это подтверждает тот факт, что пиковые всплески полной энергии для периодов 2,8; 4,8 ч не являются резонансными.
Выводы
Проведенное численное исследование показало, что значительные колебания уровня воды в Азовском море могут вызываться довольно слабым внешним воздействием на водную поверхность. При этом колебания имеют не обязательно резонансный характер, а значительные возмущения водной поверхности наблюдаются уже в первые четыре – семь периодов колебаний внешней силы. При ветровом воздействии и при воздействии атмосферным давлением на поверхность Азовского моря получаются аналогичные результаты.
Результаты, полученные в представленной работе, согласуются с результатами, полученными другими авторами, хотя и не имеют точного с ними совпадения. Это объясняется применением разных математических моделей, а также отличием в аппроксимации самого Азовского моря, что влияет на значения собственных колебаний модели исследуемого объекта.
1. Опасные штормовые нагоны и разрушение берегов Азовского моря / Л. А. Беспалова [и др.] // Наука Юга России. 2019. Т. 15, № 2. С. 29–38. EDN JRLJAH. https://doi.org/10.7868/S25000640190204
2. Черкесов Л. В., Шульга Т. Я. Исследование влияния параметров барических образований на свободные и вынужденные колебания уровня и течения в Азовском море // Морcкой гидрофизический журнал. 2016. № 4. С. 13–26. EDN WINRBD. https://doi.org/10.22449/0233-7584-2016-4-13-26
3. Матишов Г. Г., Инжебейкин Ю. И. Численные исследования сейшевых колебаний уров-ня Азовского моря // Океанология. Физика моря. 2009. Т. 49, № 4. С. 485–493. EDN KWIFHR.
4. Фомин В. В., Лазоренко Д. И., Иванча Е. В. Численное моделирование сейш в Балаклав-ской бухте // Экологическая безопасность прибрежной и шельфовой зон моря. 2017. № 3. С. 32–39. EDN ZMZFVV.
5. Манилюк Ю. В., Черкесов Л. В. Исследование свободных колебаний жидкости в ограниченном бассейне, представляющем приближенную модель Азовского моря // Морской гидрофизический журнал. 2016. № 2. С. 16–26. EDN TSADQW. https://doi.org/10.22449/0233-7584-2016-2-16-26
6. Филиппов Ю. Г. Свободные колебания уровня Азовского моря. // Метеорология и гид-рология. 2012. № 2. С. 78–82. EDN OPLEGT.
7. Иванов В. А., Черкесов Л. В., Шульга Т. Я. Исследование свободных колебаний уровня Азовского моря, возникающих после прекращения длительного действия ветра // Мор-ской гидрофизический журнал. 2015. № 2. С. 15–25. EDN VDVDCJ. https://doi.org/10.22449/0233-7584-2015-2-15-25
8. Иванов В. А., Шульга Т. Я. Численный анализ влияния параметров перемещающихся атмосферных фронтов на течения, свободные и вынужденные колебания уровня Азов-ского моря // Прикладная механика и техническая физика. 2018. Т. 59, № 5 (351). С. 166–177. https://doi.org/10.15372/PMTF20180519. EDN XZIYAX.
9. Черкесов Л. В. Шульга Т. Я. Численный анализ влияния перемещающихся барических полей на течения, свободные и вынужденные колебания уровня в Азовском море // Эко-логический вестник научных центров Черноморского экономического сотрудничества. 2016. Т. 13, № 2. С. 99–110. EDN WDKVXZ.
10. Сгонно-нагонные колебания уровня воды устьевой области Дона: численное моделиро-вание и сценарии изменения / А. Л. Чикин [и др.] // Наука Юга России. 2017. Т. 13, № 3. С. 39–49. EDN ZFIGHD. https://doi.org/10.23885/2500-0640-2017-13-3-39-49
11. Luettich R. A., Westerink J. J. Formulation and numerical implementation of the 2D/3D ADCIRC. Finite element model version 44.XX. Notre Dame, 2004. 74 p.
12. Расчет и анализ морских наводнений в дельте р. Дон / В. В. Фомин, Д. В. Алексеев, Е. М. Лемешко, Д. И. Лазоренко // Метеорология и гидрология. 2018. № 2. С. 45–54. EDN YPPJNA.
13. Филиппов Ю. Г. Об одном способе расчета морских течений // Труды Государственного океанографического института. 1970. № 103. С. 87–94.
14. Филиппов Ю. Г. Моделирование сейшевых колебаний уровня Азовского моря // Труды Государственного океанографического института. 2011. № 213. С. 146–154. EDN PXRVDZ.

















