Россия
Россия
Россия
Россия
УДК 551.2.02 Практическая и экспериментальная работа
УДК 551.556.8 Действие на водную поверхность
УДК 551.553.8 Штормы
Цель. Поле ветровых волн нестационарно из-за изменчивости факторов волнообразования, та-ких как ветровое воздействие и непрерывно протекающие процессы нелинейных взаимодействий волн. Однако во многих практических задачах предполагается, что процесс волнения, описывае-мый некоторой временно́й записью волнения, является квазистационарным. В мировой практи-ке нет общепринятой длины волновой записи, для которой бы выполнялись условия однородно-сти и стационарности поля волн. Поэтому основной целью работы является оценка промежутка стационарности поля волн на основе данных натурных прямых контактных измерений, прове-денных на Черном море в различные годы и сезоны на глубокой воде и в прибрежной зоне. Методы и результаты. Для анализа использовались данные двух натурных долговременных экспериментов, проведенных в Черном море. Волнение в открытом море измерялось с помо-щью Directional waverider buoy, в прибрежной зоне буем Spoondrifter spotter и контактным струнным волнографом резистентного типа, установленным на специализированной морской эстакаде у берега. Применялись методы спектрального анализа. В качестве характеристики од-нородности ветрового волнения рассматривалась ширина спектрального пика, определенная как параметр пиковатости. Волновые записи с повышенными значениями параметра пиковатости, характеризующиеся узкополосным спектральным распределением, были отнесены к случаям квазистационарного волнения с однородным спектральным составом, приближающимся к регу-лярному волновому процессу. В результате были получены характерные временны́е интервалы, для которых возможно принять поле волн однородным и близким к стационарному. Выводы. Вне зависимости от условий волнообразования промежуток стационарности волнения в Черном море может быть принят равным 8–12 мин. Эти оценки совпадают для глубоководной и прибрежной частей моря и качественно соответствуют теоретическим.
ветровые волны, параметры волн, длина записи волнения, однородность поля волн, спектр волн, промежуток стационарности
Введение
Знание основных параметров ветрового волнения и закономерностей их пространственно-временно́й изменчивости является актуальным для широкого круга задач, связанных с вопросами прогноза волнения, оценки воздействия на гидротехнические объекты в прибрежной зоне, минимизации возможных эксплуатационных рисков при проведении морских операций и пр. Поле ветровых волн нестационарно из-за изменчивости факторов волнообразования, прежде всего таких, как ветровое воздействие и непрерывно протекающие процессы нелинейных взаимодействий волн. Однако во многих практических задачах, чтобы определить статистические свойства волн, делаются предположения, что процесс волнения, описываемый временно́й записью волнения, является стационарным (или квазистационарным). Это означает, что статистические свойства волнения не зависят от начала времени измерения. Требование стационарности необходимо, например, для описания распределения вероятности высот волн, представляющего собой долю времени, в течение которого высоты волн, измеренные во временно́м ряду, не превышаются. Временной промежуток стационарности волнения важен также при верификации спутниковых измерений волн по контактным данным в условиях несовпадения момента пролета спутника и времени регистрации волн. Однако в действительности волнение можно считать стационарным только в течение ограниченного периода в месте сбора данных. Как отмечается в международном «Руководстве для береговых инженеров», ветровые волны можно считать приблизительно стационарными только в течение нескольких часов (3 ч или меньше), после чего их свойства, как ожидается, изменятся .
На временно́м промежутке стационарности характеристики записи волнения не должны сильно меняться, если запись была немного короче или длиннее и выборка была начата на некоторую долю времени раньше или позже. Если приведенные выше предположения не выполняются, это означает, что волнение нестационарно и не может быть охарактеризовано простым статистическим описанием.
С точки зрения статистического описания реальное нерегулярное волновое поле полностью характеризуется двумерным частотно-направленным спектром [1]. Спектр морской поверхности не имеет строгой математической формы, однако в практике океанографических исследований применяются различные эмпирические модели, аппроксимирующие спектр волнения. Они называются параметрическими моделями спектра и полезны для обычных инженерных приложений. Одной из наиболее удачных и широко применяемых аппроксимаций частотного спектра поверхностного волнения является спектр JONSWAP, предложенный в 1973 г. по результатам натурных наблюдений в Северном море и в обобщенном виде записывающийся в виде [2]
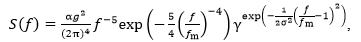
где 
– постоянная Филлипса ( = 0,0081); fm – частота максимума спектра; 
– параметр формы (peak enhancement coefficient). Параметр является крайне важной характеристикой спектра, контролирующей его форму и обусловливающей распределение волновой энергии в частотном диапазоне.
На рис. 1 приведен пример спектров поверхностного волнения и соответствующих JONSWAP-аппроксимаций. Экспериментальные спектры получены на Черном море волнографом Datawell Waverider [3]. Для ветровых волн, спектры которых представлены на рис. 1, а и b, значительные высоты волн hs и частоты пика спектра fp одинаковы (~ 2,6 м и 0,15 Гц соответственно), но параметры формы различаются (2,6 и 5,1).
Другими словами, из рис. 1 следует, что при одинаковых интегральных характеристиках волнения (hs и fp) распределение спектральной энергии по частотам существенно различается. Можно сказать, что при большем параметре наблюдается концентрация волновой энергии в области основного максимума спектра. При отсутствии одиночных аномальных по высоте волн в записи волнения это означает, что волнение однородно по спектральному составу, так как имеет преимущественно одну частоту и может рассматриваться как близкое к регулярному стационарному волнению. Приведенный пример также показывает, что высота или период не могут служить показателями регулярности (однородности, стационарности) волнения, так как ничего не говорят о его спектральном составе. Ширина спектра, косвенно характеризующаяся параметром формы является достаточно информативным показателем и используется, например, при оценке распределения высот волн [4]. Заметим, что при спектральном анализе записи волнения важно, чтобы эта запись удовлетворяла также предположениям стационарности поля волн. Например, «Руководство для береговых инженеров» 1 рекомендует использовать для спектрального анализа волновые записи длиной от 17 до 68 мин.
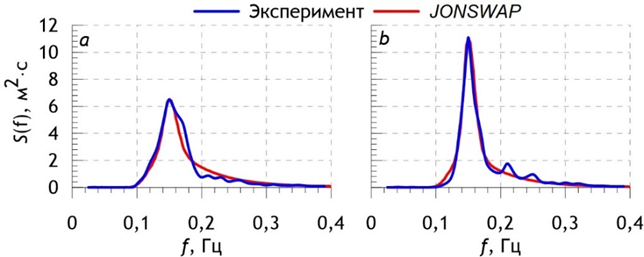
Р и с. 1. Экспериментальные спектры ветрового волнения и их аппроксимации спектром JONSWAP при hs = 2,6 м, fp = 0,15 Гц, 
= 2,6 (a) и = 5,1 (b)
F i g. 1. Experimental spectra of wind waves and their approximations by the JONSWAP spectrum at hs = 2.6 m, fp = 0.15 Hz, = 2.6 (a) and = 5.1 (b)
В международной инженерной практике существует понятие «промежуток квазистационарности» волнового процесса, принимаемый равным 20 мин и соответствующий неизменным внешним факторам волнообразования Термин устоявшийся и широко используемый при проведении инструментальных наблюдений за параметрами ветрового волнения. Большинство специализированных морских волнографов регистрируют именно 20-минутные записи возвышений свободной поверхности, по которым в дальнейшем рассчитываются основные параметры волнения и проводятся статистические обобщения. Однако эти рекомендации традиционно касаются только волн на глубокой воде. Корректность использования термина «промежуток квазистационарности» для ветрового волнения в прибрежной зоне остается под вопросом. Отметим, что в некоторых случаях программное обеспечение волномерных буев может рассчитывать волновые статистики на основе более длинных, 30-минутных серий измерений (например, буй Datawell). В научной литературе, помимо 20-минутного ряда наблюдений, при построении спектральных и статистических характеристик волнения используют ряды волновых записей длиной 5, 6, 10 и 15 мин, поскольку считается, что более длинные ряды могут быть нестационарными [5–7]. По теоретическим оценкам, интервал квазистационарности составляет от 10 до 100 характерных временны́х масштабов периодов волны τ, где 1 < τ < 10 c [5].
Помимо длины записи, точность спектральных оценок также зависит от дискретности записи (шага по времени) и метода стягивания спектрального окна в целях соблюдения баланса между степенью сглаженности спектра и детализацией его основных составляющих. При этом выбор самой формы спектрального окна оказывает незначительное влияние [8].
Как было отмечено выше, гипотеза о стационарности служит теоретической основой для оценки волновой статистики по данным натурных измерений. Неявно предполагается, что она выполняется и действительна для любого состояния моря. Однако детальная проверка на практике этого предположения по большому массиву натурных данных, соответствующих разным условиям волнообразования, никогда не проводилась. Поэтому основной целью работы является оценка промежутка стационарности поля волн на основе данных натурных прямых контактных измерений, проведенных на Черном море в различные годы и сезоны на глубокой воде и в прибрежной зоне.
Натурные данные и методы исследования
Для анализа использовались данные двух натурных экспериментов, проведенных в разное время в Черном море. Первый эксперимент проводился с 1996 по 2003 г. и охватывал все сезоны. Измерения параметров ветрового волнения были выполнены в рамках международной программы NATO TU‑WAVES. Буй Directional waverider был установлен в открытом море в районе г. Геленджика. Координаты точки установки 44°30¢40 с. ш., 37°58¢70 в. д. Глубина места 85 м, что для всех наблюдавшихся волн (исключая высоты аномальных волн) соответствует условиям глубокой воды. Каждые три часа, а при превышении значительной высоты волн отметки в 1,5 м каждый час буй передавал 20-минутные записи возвышений уровня свободной поверхности с дискретностью 1,28 Гц. Диапазон измеренных высот волн изменялся от 0,1 до 12 м, периодов – от 2,5 до 11,4 с. Более подробное описание отдельных этапов этого эксперимента и полученных результатов можно найти в [9]. В апреле 1998 г. работа буя была переключена в режим непрерывной записи, составившей 70 ч. Эта запись была использована для детального анализа.
Второй эксперимент был проведен в сентябре – октябре 2016 г. в береговой зоне Черного моря в пос. Шкорпиловцы вблизи г. Варны. Волнение измерялось с помощью трех буев Spoondrifter spotter. Буй Spoondrifter spotter ведет запись хронограмм трех компонент его смещения с частотой 2,5 Гц. Одновременно велись измерения решеткой из четырех контактных струнных волнографов резистентного типа, установленной на специализированной морской эстакаде на расстоянии 200 м от берега.
Для анализа были использованы данные буя, заякоренного в точке 42°95¢85 с. ш. и 27°90¢35 в. д. на глубине 12 м, и данные струнного волнографа, расположенного на конце эстакады (глубина 4,5 м) (рис. 2). Диапазон измеренных во время эксперимента высот волн составлял от 0,1 до 3 м, периодов – от 2,5 до 10 с.
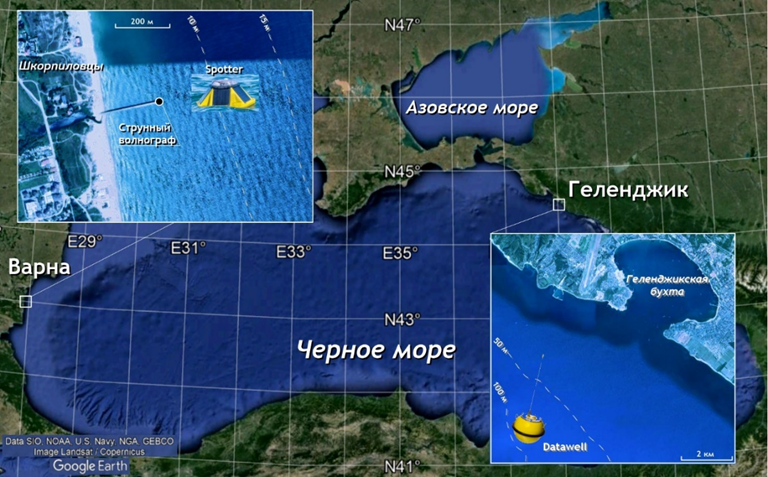
Р и с. 2. Положение волновых регистрирующих приборов
F i g. 2. Location of wave recording devices
Основные параметры волнения определялись в результате анализа частотных спектров и соответствующих моментов. Спектральные моменты представляются в виде
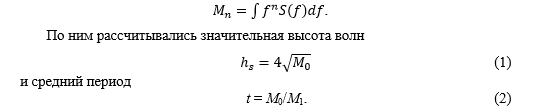
В качестве характеристики нерегулярности ветрового волнения рассматривалась ширина спектрального пика, определяемая в руководстве как
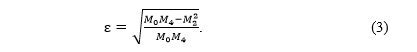
Значения параметра 
изменяются от 0 (соответствует узкому спектру регулярного волнения) до 1, что характерно для широкого спектра, представленного нерегулярным волновым полем. Поскольку ширина спектра в формуле (3) сильно зависит от качества исходных данных, в работе [10] в качестве альтернативы был предложен параметр пиковатости спектра (peakedness parameter), определяемый соотношением
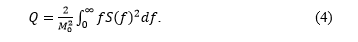
Значения параметра пиковатости Q больше единицы. Чем больше значение Q, тем более узкополосный спектр.
Как уже отмечалось во введении, узкий спектр свидетельствует о достаточно однородном по спектральному составу поле волн, близком к регулярному волнению, обладающим свойством стационарности.
Для построения спектра были использованы параметрический метод спектрального анализа (волны на глубокой воде) и построение спектра методом Уэлча с окном Хэмминга (волны в береговой зоне) [11]. Метод Уэлча усредняет спектральные оценки по перекрывающимся сегментам волновой записи. Таким образом, частотное разрешение полученных спектральных оценок определяется длиной этих отрезков. В проведенном исследовании оно было постоянным, равным 0,02 Гц и не зависело от длины волновой записи. Такое же разрешение по частоте было выбрано для параметрического метода. Были сделаны оценки влияния метода построения спектра на получаемые спектральные характеристики.
Проведенный анализ показал, что спектральные оценки практически не зависят от метода построения спектра, в частности от формы окна сглаживания, но существенно зависят от частотного разрешения. Это полностью соответствует теоретическим представлениям, изложенным в [8]. Например, частотное разрешение 0,1 Гц не дает различий в спектральных оценках при любой длине записи, так как получаемый спектр будет слишком сглаженным, широким и иметь практически одну и ту же форму. Как отмечено в [8, 11], выбор параметров спектрального оценивания определяется компромиссом между разрешающей способностью и сглаживанием спектра с учетом целевых характеристик исследуемого процесса. В нашем исследовании разрешение 0,02 Гц было выбрано таким образом, чтобы на спектре четко выявлялась вторая нелинейная гармоника, определяющая многие динамические процессы в береговой зоне моря [12].
Дополнительно для условий береговой зоны были выполнены оценки изменчивости высших волновых моментов, которые являются своеобразными показателями нелинейных взаимодействий в волнах и часто используются в инженерных и прогностических моделях, например при определении направления и величины расхода донных отложений наносов в береговой зоне [13–15] или для оценки вероятности аномально высоких волн [16].
Рассматривались третьи волновые моменты – асимметрия относительно вертикальной оси Аs (англ. asymmetry), асимметрия относительно горизонтальной оси Sk (англ. skewness) – и четвертый волновой момент K (англ. kurtosis), вычисляемые по формулам, предложенным в [16; 17, p. 1726]:
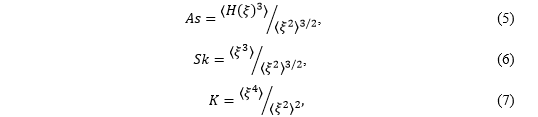
где ξ – хронограммы возвышений свободной поверхности (волны); Н – преобразование Гильберта; угловые скобки означают осреднение по времени.
Результаты и обсуждение
Однородность поля волн во времени на глубокой воде
Проанализируем непрерывную 70-часовую запись буя Datawell. На ее основе сформируем сто сорок 30-минутных серий возвышений свободной поверхности. Для каждой 30-минутной реализации вначале берутся первые 5 минут и для этой 5-минутной записи рассчитываются спектральные характеристики. Далее будем увеличивать длину L хронограммы волнения до 30 мин с шагом 1 мин. Пример обработки одной 30-минутной записи приведен на рис. 3.
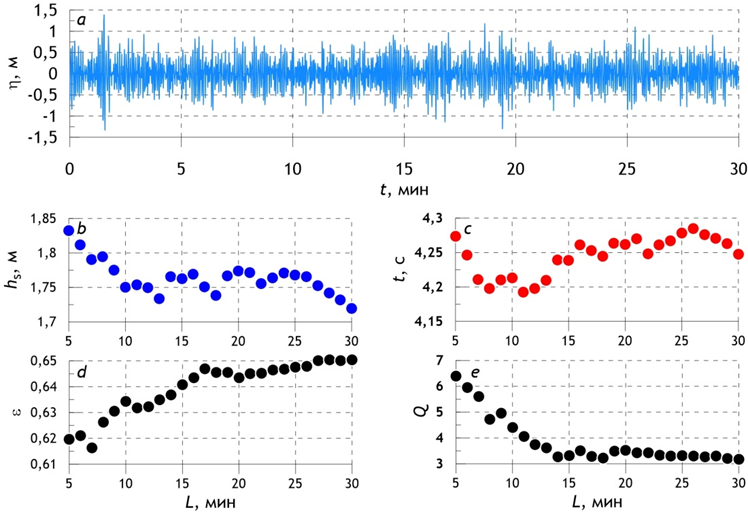
Р и с. 3. Возвышение свободной поверхности (а), значительные высоты волн (b), средние периоды (c), ширина спектра (d) и параметр пиковатости (e) для последовательных хронограмм длиной L
F i g. 3. Free surface elevation (a), significant wave heights (b), average periods (c), spectrum width (d), and peakedness parameter (e) for successive chronograms of L length
Как видно из рис. 3, увеличение длины хронограммы с 5 до 30 мин несущественно влияет на рассчитанные значительные высоты волн (1) и средние периоды (2). Ширина спектра (3) (рис. 3, d) вначале увеличивается, а после L = 17 мин становится практически постоянной. При этом в абсолютном выражении параметр меняется довольно незначительно. По сравнению с ним параметр Q немного увеличивается при длине хронограммы L, равной 8–9 мин, и опять уменьшается при увеличении длины хронограммы до 14 мин. При увеличении длины хронограммы L с 14 до 30 мин значение параметра пиковатости почти не меняется.
Такие особенности показаны только для одной конкретной серии наблюдений. Для получения статистически значимых результатов было сделано обобщение по всем имеющимся записям (сто сорок 30-минутных хронограмм волнения).
На рис. 4, а приведены графические оценки, демонстрирующие положение среднего значения для ширины спектра, а также 10, 25, 75 и 90%-ный квантили распределений. На рис. 4, b показаны средние значения и 95%-ные доверительные интервалы для среднего значения (серая область). Хорошо видно, что статистические характеристики ширины спектра не зависят от длины реализации (рис. 4). Можно сказать, что ширина спектра, определяемая формулой (3), для наших целей малоинформативна и не пригодна для анализа нерегулярности волнения.
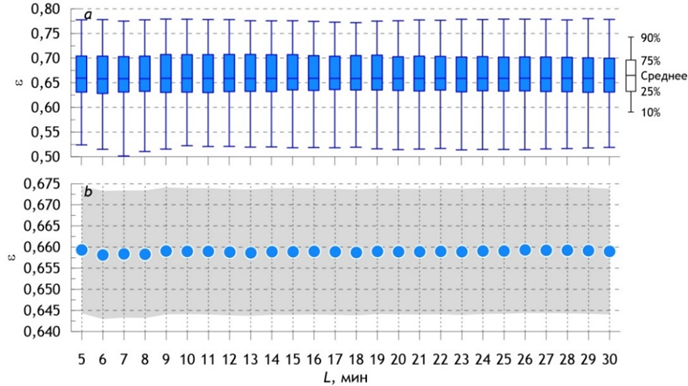
Р и с. 4. Статистические характеристики распределений значений ширины спектра (а), а также средние значения ширины спектра (b) для последовательных серий возвышений свободной поверхности длиной L
F i g. 4. Statistical characteristics of the distributions of spectrum width values (a) as well as the average spectrum width values (b) for successive series of free surface elevations of L length
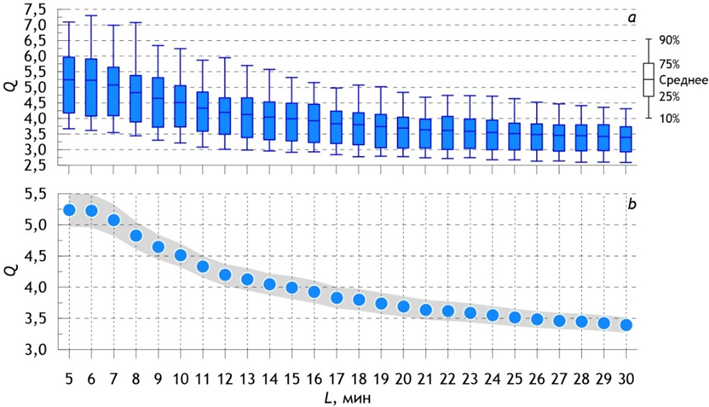
Р и с. 5. Статистические характеристики распределений значений параметра пиковатости (а), а также средние значения ширины спектра (b) для последовательных серий длиной L, равной 5, 6, …, 30 мин
F i g. 5. Statistical characteristics of the distributions of peakedness parameter values (a) as well as the average spectrum width values (b) for successive series of L length equal to 5, 6, …, 30 min
На рис. 5 представлены аналогичные графики для параметра пиковатости Q, вычисленные по формуле (4). Как видно из рис. 5, на участке, где длина хронограммы L увеличивается с 6 до 12 мин, наблюдается достаточно резкое уменьшение среднего значения параметра пиковатости. При длине хронограммы L > 12 мин параметр Q также уменьшается, но гораздо медленнее. При длине хронограммы L > 22 мин Q почти не изменяется, что, по-видимому, связано с увеличением ширины спектра, не позволяющим детализировать его форму. Отметим также небольшой размах 95%-ных доверительных интервалов (серая область на рис. 5, b) для среднего значения.
Для расширения статистической базы исследования используем архивные данные 20-минутных записей возвышений свободной поверхности за 1998 г., которые охватывают весь диапазон наблюдаемых состояний ветрового волнения – от слабого до штормового. Общее число таких записей – 1100.
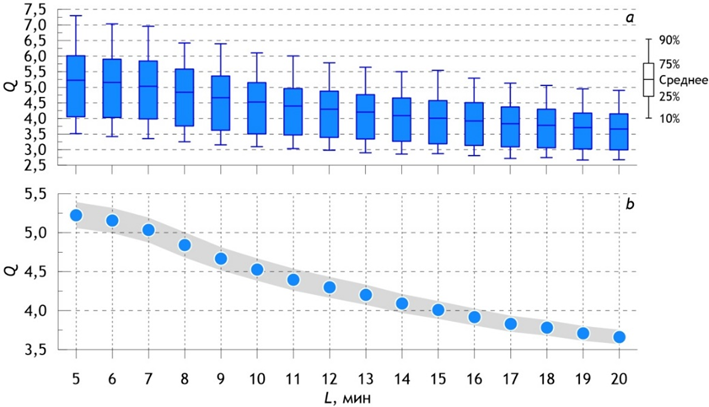
Р и с. 6. Статистические характеристики распределений значений параметра пиковатости (а), а также средние значения ширины спектра (b) для последовательных серий возвышений свободной поверхности длиной L
F i g. 6. Statistical characteristics of the distributions of peakedness parameter values (a) as well as the average spectrum width values (b) for successive series of free surface elevations of L length
На рис. 6 представлены результаты анализа всех этих записей. Анализ показывает, что с увеличением длины хронограммы от 7 до 20 мин параметр пиковатости уменьшается, причем этот процесс имеет двухстадийный характер: при увеличении длины хронограммы от 7 до 12 мин наблюдается быстрое убывание параметра, а при дальнейшем увеличении до 20 мин – более медленное, что согласуется с закономерностями, выявленными для непрерывной записи (рис. 6). Значения параметра Q остаются относительно высокими для длины записи примерно до 8 мин, что свидетельствует об узком спектре, позволяющем рассматривать волны как близкие к регулярным. Исходя из этого, можно заключить, что волновое поле может считаться однородным по спектральному составу за промежуток времени до 8 мин. Учитывая, что при увеличении длины записи до 12 мин значения параметра Q хотя и уменьшаются, но остаются еще высокими, можно предположить, что поле волн будет близким к однородному не более 12 мин.
Таким образом, параметр пиковатости позволяет достаточно эффективно исследовать спектральную структуру волнения с точки зрения его нерегулярности. При этом записи возвышений свободной поверхности длиной до 12 мин могут быть отнесены к случаям квазиоднородного по спектральному составу волнения и условно рассматриваться как близкие к стационарному волнению. Заметим, что полученные результаты не зависят от условий волнообразования и степени развития ветрового волнения.
Однородность поля волн во времени в береговой зоне моря
Результаты, полученные в предыдущем разделе для волн на глубокой воде, полностью подтверждаются для волн в береговой зоне моря. Рассмотрим их на примере двух суточных хронограмм. Для того чтобы подробнее оценить влияние условий волнообразования были выбраны две 24-часовые записи волнения, соответствующие увеличению (3–4 ноября 2018 г.) и уменьшению (7–8 ноября 2018 г.) высоты волн (рис. 7).
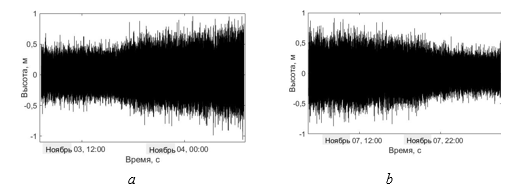
Р и с. 7. Используемые для анализа хронограммы волнения, зарегистрированные буем Spoondrifter в береговой зоне Черного моря 3–4 (а) и 7–8 (b) ноября 2018 г.
F i g. 7. Wave chronograms recorded by the Spoondrifter buoy in the Black Sea coastal zone on November 3–4 (a) and 7–8 (b) in 2018, and used for analysis
Поскольку буй меняет свое положение относительно якоря в зависимости от направления ветра и течения, то для оценки влияния его подвижности на получаемые данные были использованы синхронные записи возвышений свободной поверхности стационарного струнного волнографа, расположенного на конце эстакады на глубине 4,5 м, за 7–8 ноября 2018 г.
На рис. 8 представлены изменения значительной высоты волн, среднего периода и параметра Q в зависимости от длины записи, используемой для оценки, для буя и стационарного волнографа.
Видно, что увеличение длины записи слабо влияет на получаемые значения высоты волн и среднего периода. При увеличении длины записи более 12 мин различия минимальны. Так же, как и для волн на глубокой воде, параметр пиковатости спектра резко уменьшается с увеличением длины записи примерно с 7–9 до 12 мин и далее изменяется незначительно. Наблюдающиеся изменения при длине записи менее 8 мин (рис. 8, а и b) могут быть связаны с особенностями этой конкретной записи. Возможно, ее длина слишком мала, чтобы минимизировать влияние подвижности буя, поскольку такие изменения не наблюдаются для измерений струнным волнографом. Эти отклонения не наблюдаются и при осреднении по всем реализациям.
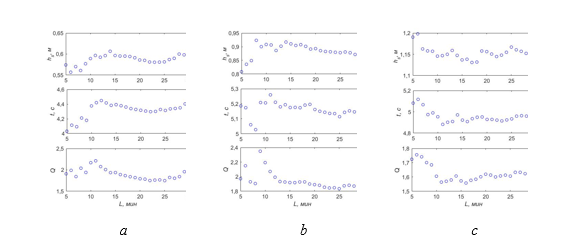
Р и с. 8. Зависимости значительной высоты волн, среднего периода и параметра пиковатости спектра от длины хронограммы L по данным буя 3 (а) и 7 (b) ноября 2018 г. и стационарного волнографа 7 ноября 2018 г. (с)
F i g. 8. Dependences of significant wave height, average period and spectrum peakedness parameter on the chronogram length L based on the buoy data from November 3 (a) and 7 (b), 2018 and the stationary wave recorder data from November 7, 2018 (c)
Средние значения параметра пиковатости для выбранных 24-часовых записей приведены на рис. 9.
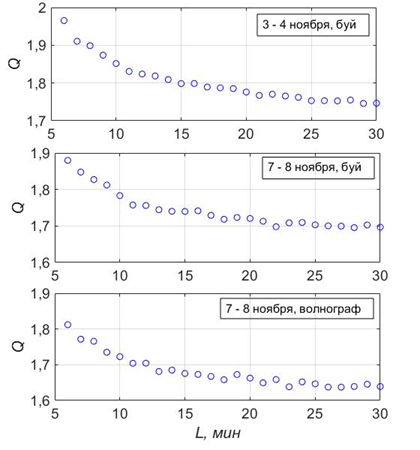
Р и с. 9. Зависимость средних значений параметра пиковатости спектра Q от длины L последовательных серий возвышений свободной поверхности в береговой зоне моря
F i g. 9. Dependence of the average values of spectrum Q peakedness parameter upon the L length of successive series of free surface elevations in the Black Sea coastal zone
Как и в случае волн на глубокой воде (см. рис. 6), уменьшение параметра пиковатости с увеличением длины хронограммы происходит на двух основных временны́х отрезках: быстрое убывание при увеличении длины записи от 6 до 12 мин и более медленное при дальнейшем увеличении длины записи до 20 мин. Абсолютные значения параметра Q остаются относительно высокими (узкий спектр) для записей длиной менее 8 мин, что позволяет считать волновое поле однородным по спектральному составу примерно 8 мин или квазиоднородным не более 12 мин. Увеличение длины записи до более чем 20 мин не позволяет выявить особенности формы спектра и дает почти одинаковые значения параметра Q.
Таким образом, независимо от условий волнообразования и распространения волн (глубокая вода или береговая зона) приблизительное время однородности и, следовательно, стационарности записи возвышений свободной поверхности будет около 8 мин. Длину записи до 12 мин можно приближенно считать однородной (квазистационарной). Полученные оценки полностью соответствуют теоретическим [5]. Действительно, так как рассмотренные волновые условия имели характерный временной период (период пика спектра) от 5 до 7 с, то, согласно теоретическим оценкам, максимальное время квазистационарности будет составлять 100 характерных периодов, или от 500 до 700 с, т. е. примерно от 8 до 12 мин.
Анализ высших спектральных моментов
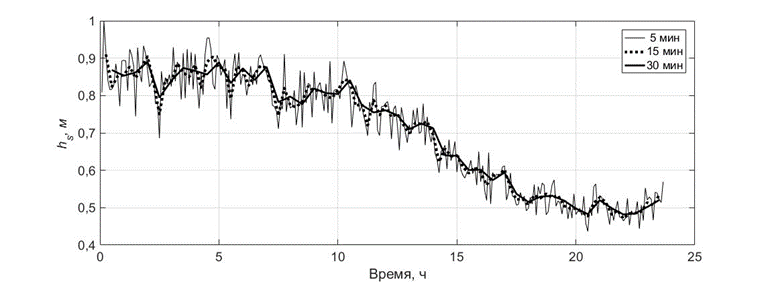
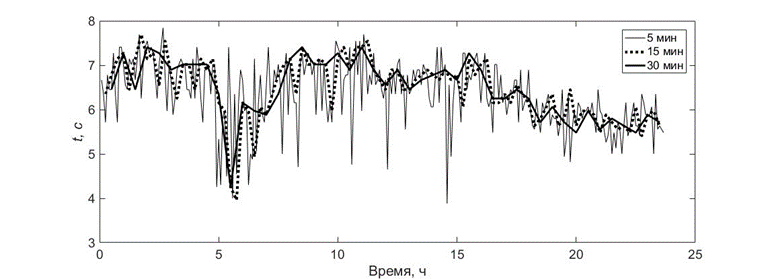
Рассмотрим, как влияет длина записи на получаемые оценки высоты волн, среднего периода и значения высших волновых моментов, определяющих форму волн, на примере суточной записи затухающего волнения, сделанной буем 7–8 ноября 2018 г. (рис. 10, 11).
a
b
Р и с. 10. Изменение значительной высоты волны (а) и среднего периода волнения (b) по хронограммам разной длины для 24-часовой записи 7–8 ноября 2018 г.
F i g. 10. Changes in significant wave height (a) and average wave period (b) based on the chronograms of different lengths for a 24-hour record made on November 7–8, 2018
В целом тенденции изменения выбранных волновых параметров за 24 ч, полученные по хронограммам разной длины, одинаковые. Однако чем меньше длина хронограммы, выбранной для оценки, тем больше абсолютные изменения для всех параметров. При увеличении длины записи, используемой для вычисления, разброс абсолютных значений уменьшается. Так, разброс значений для записей длиной 5 и 30 мин составляет до 10 % в изменении высоты и до 50 % в изменениях среднего периода волн независимо от стадии затухания волнения. Значения выбранных параметров волн, вычисленные по записям длиной от 10 до 20 мин, близки и различаются в пределах 2–3 %. Значения, полученные по 30-минутным записям, более сглаженные.
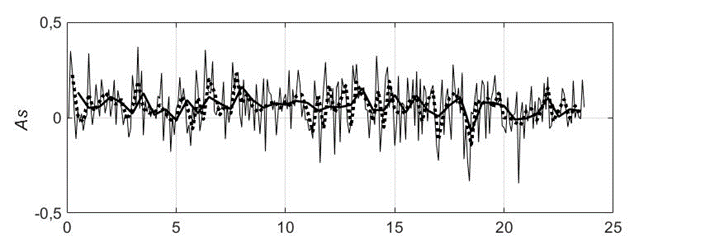
Параметры формы волны, например волновая асимметрия относительно вертикальной и горизонтальной осей, получаемая по 30‑минутным хронограммам, практически не принимает отрицательных значений, что может привести к некорректным оценкам направления переноса наносов.
a
b
c
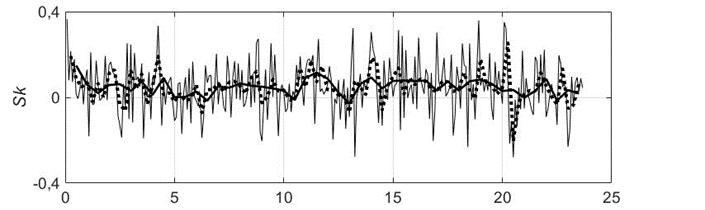
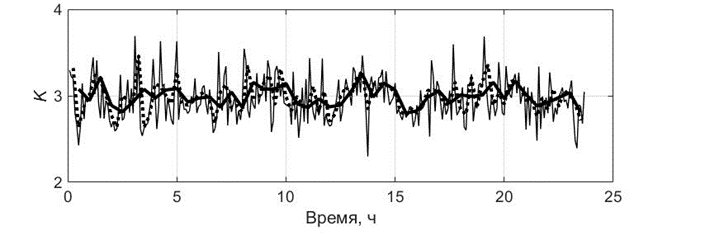
Р и с. 11. Изменение волновой асимметрии, описываемой формулами (5)–(7), вычисленной по хронограммам разной длины для 24-часовой записи 7–8 ноября 2018 г.: a – As; b – Sk; c – K
F i g. 11. Change in wave asymmetry described by formulas (5)–(7) and calculated using the chronograms of different lengths for a 24-hour record made on November 7–8, 2018: a – As; b – Sk; c – K
Выводы
Результаты исследования показали, что вне зависимости от условий волнообразования промежуток стационарности волнения в Черном море может быть принят равным 8–12 мин. Для глубоководной и прибрежной частей моря эти оценки совпадают. Их качественное соответствие теоретическим оценкам позволяет предположить универсальность этого результата для всего Мирового океана.
Оценки высших волновых моментов и формы спектра нерегулярного волнения с помощью параметра пиковатости Q демонстрируют бо́льшую изменчивость, если рассчитаны по волновой записи, не превышающей длины промежутка стационарности.
1. Longuet-Higgins M. S., Cartwright D. E., Smith N. D. Observation of the directional spectrum of sea waves using the motions of a floating buoy // Ocean Wave Spectra : proceedings of a conference. Easton, Maryland, 1961. P. 111–132.
2. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP)' / K. Hasselmann [et al.] // Erganzungsheft zur Deutschen Hydrographischen Zeitschrift Reihe A. 1973. A(80), nr. 12. Hamburg : DHI, 95 p.
3. Дивинский Б. В. Результаты измерений параметров поверхностных волн с помощью буя в районе г. Геленджик // Динамические процессы береговой зоны моря. Москва : Науч-ный мир, 2003. Раздел 3.1. C. 70–91.
4. Tayfun M. A. Effects of spectrum band width on the distribution of wave heights and periods // Ocean Engineering. 1983. Vol. 10, iss. 2. P. 107–118. https://doi.org/10.1016/0029-8018(83)90017-3
5. Ефимов В. В., Полников В. Г. Численное моделирование ветрового волнения. Киев : На-укова думка, 1991. 238 c.
6. Трубкин И. П. Методика расчета и некоторые результаты определения двумерного энер-гетического спектра случайного поля поверхностных волн в прибрежной зоне моря // Экологические системы и приборы. 2003. № 9. C. 47–53.
7. Вапняр М. У., Татлыева 3. И. О характере многолетнего распределения высот волн на Каспийском море // Труды ГОИН. 1989. Вып. 188. С. 132–137.
8. Дженкинс Г., Ваттс Д. Спектральный анализ и его приложения. Вып. 1. Москва : Мир, 1971. 316 с.
9. Экстремальное волнение в северо-восточной части Черного моря в феврале 2003 г. / Б. В. Дивинский [и др.] // Океанология. 2003. Т. 43, № 6. C. 948–950. EDN OOGQSB.
10. Goda Y. Numerical Experiments on Wave Statistics with Spectral Simulation // Report of the Port and Harbour Research Institute. 1970. Vol. 9, no. 3. P. 3–57.
11. Marple Jr. S. L. Digital spectral analysis with applications. Englewood Cliffs, N. J. : P T R Prentice-Hall, 1987. 492 p.
12. Сценарии нелинейной трансформации волн в береговой зоне моря / Я. В. Сапрыкина [и др.] // Океанология. 2013. Т. 53, № 4. С. 476–485. EDN QMFYYD. https://doi.org/10.7868/S0030157413040126
13. Bailard J. A. An energetics total load sediment transport model for a plane sloping beach // Journal of Geophysical Research: Oceans. 1981. Vol. 86, iss. C11. P. 10938–10954. https://doi.org/10.1029/JC086iC11p10938
14. Ruessink B. G., van den Berg T. J. J., van Rijn L. C. Modeling sediment transport beneath skewed asymmetric waves above a plane bed // Journal of Geophysical Research: Oceans. 2009. Vol. 114, iss. C11. C11021. https://doi.org/10.1029/2009JC005416
15. Saprykina Y. The influence of wave nonlinearity on cross-shore sediment transport in coastal zone: experimental investigations // Applied Sciences. 2020. Vol. 10, iss. 12. 4087. https://doi.org/10.3390/app10124087
16. Relation between occurrence probability of freak waves and kurtosis/skewness in unidirectional wave trains under single-peak spectra / Lei Wang [et al.] // Ocean Engineering. 2022. Vol. 248. 110813. https://doi.org/10.1016/j.oceaneng.2022.110813
17. Elgar S. Relationships involving third moments and bispectra of a harmonic process // IEEE Transactions on Acoustics, Speech, and Signal Processing. 1987. Vol. 35, no. 12. P. 1725–1726. https://doi.org/10.1109/TASSP.1987.1165090
