Введение

При решении задач гидродинамики традиционно используются два подхода – эйлеров и лагранжев. Эти методы, как правило, эффективны для разных классов задач, оба имеют широкие сферы применения, могут взаимодополнять друг друга для получения более полной информации о процессах, происходящих в жидкости. При построении большинства современных моделей циркуляции океана, а также при описании общей динамики сплошной среды используется в основном эйлеров подход. В отличие от него, лагранжев подход фокусируется на траектории движения бесконечно малой жидкой частицы под действием заданных сил. Это позволяет оценить детали отдельных течений или специфичных структур (например, поверхностных и подводных течений, океанических вихрей и т. д.) в процессе эволюции внутреннего состояния сплошной среды. При этом частицам можно придать различные свойства, в том числе характерные, например, для локального био- и антропогенеза, реального или гипотетического источника загрязнения (в том числе радиоактивного), и таким образом воспроизвести динамику распространения примеси в поле заданного течения. Поскольку при моделировании динамики океана вода часто рассматривается в двух состояниях (жидком и твердом), динамические свойства которых кардинально различаются, особый научный интерес представляет изучение транспорта частиц в рамках обеих термодинамических фаз. Насколько нам известно, на данный момент в открытом доступе не представлены модели, учитывающие подобные процессы [1].

Совместное использование эйлерова и лагранжева подходов позволяет комплексно решать задачи о циркуляции вод, распространении примесей различной природы (радиоактивных и устойчивых изотопов, растворимых и нерастворимых элементов антропогенного и естественного происхождения) и, соответственно, оценивать их влияние на окружающую среду. Подобный инструмент востребован в связи с развитием логистического и военно-политического потенциала Северного морского пути  и в целом всего Арктического региона  Так, в ходе освоения ресурсов Северного Ледовитого океана (СЛО) уже активно используются плавучие атомные электростанции, что в силу различных факторов риска обусловливает необходимость детального изучения их воздействия на окружающую среду [2]. Особое внимание следует уделить возможным внештатным ситуациям, связанным с попаданием радиоактивных изотопов в воды СЛО, что требует проведения исследования для оценки долговременных последствий [3]. Для решения этих задач оптимально подходит инструмент, основанный на совместной лагранжево-эйлеровой модели океана. В связи с этим разработка такого инструмента на базе отечественных программных продуктов приобретает особую актуальность 

При построении совместной лагранжево-эйлеровой модели частицы часто принято рассматривать как пассивные трассеры, не влияющие на свойства переносящего их потока. Очевидно, первичной в такой конфигурации является именно эйлерова модель: точность и достоверность полученного в результате расчетов поля скоростей определяет достоверность прогноза транспорта частиц. Эйлерова модель динамики океана подразумевает численное решение полной системы уравнений динамики жидкости в заданной акватории с определенным разрешением расчетной области при заданной параметризации внутренних и граничных процессов. При совместном использовании с моделями льда и/или атмосферы этот подход обеспечивает высокую эффективность в прогнозировании динамики региональных и глобальных климатических процессов [4–10]. Применение таких моделей совместно с моделью лагранжева переноса представляется наиболее целесообразным, что подтверждается многочисленными реализованными моделями, представленными в обзоре [1].

Численные модели, поддерживающие лагранжев перенос частиц, можно разделить на два подкласса: автономные и синхронные. В первом случае эйлерова и лагранжева модели запускаются независимо друг от друг (как правило, последовательно). Поле скоростей, полученное в результате запуска первой модели, впоследствии используется во второй. В качестве примера реализации первого подкласса можно упомянуть TRACMASS [11], Ariane [12], CMS [13], а также модель Лагранжа на базе SibCIOM [14]. Во втором случае, как следует из названия, процесс моделирования динамики жидкости и частиц осуществляется синхронно, а полный набор данных о течении во всей расчетной области используется в лагранжевой модели на каждом временно́м шаге, то есть с максимально возможной дискретностью. Примеры реализации можно найти в моделях MRI.COM , NEMO  HYCOM [15], ROMS [16], MITgcm [17].

Автономные модели имеют ряд недостатков по сравнению с синхронными. Так, трехмерные поля скоростей всегда являются осредненными по времени (и иногда пространству), что влечет потерю точности в описании динамических процессов [1]. Хранение данных о течениях в четырехмерном массиве требует больших объемов дискового пространства. Во-первых, это ограничивает возможность исследования длительных по времени и детальных по пространству процессов. Во-вторых, процедура чтения из внешнего носителя – относительно медленный процесс, который сильно ограничивает производительность постобработки и самой автономной модели. Небольшой платой за все преимущества синхронных моделей являются такие их недостатки, как дополнительная нагрузка на ресурсы высокопроизводительной вычислительной системы и чуть большая сложность реализации.

Целью данной работы является разработка и реализация лагранжева переноса в модели динамики океана ИВМИО [18] – части программного комплекса совместного моделирования системы океан – лед – атмосфера – почва [5, 6, 9, 19]. При этом модель транспорта лагранжевых частиц должна обладать следующими особенностями: совместное с моделью динамики океана исполнение, учет переноса в двухфазной среде при моделировании системы океан – лед, инкорпорирование частиц по заданным координатам и в заданное время, поддержка разделения частиц на группы согласно индивидуальным свойствам (время жизни, плавучесть, условие прилипания в придонном слое), общее количество частиц до 10⁶.

Данные и методы

Совместная модель океан – лед. Реализация синхронной модели лагранжева переноса напрямую зависит от «материнской» эйлеровой модели и особенностей ее устройства. В рамках данной работы была поставлена задача создания модели транспорта частиц в двухфазной среде, что подразумевает представление особенно важных с точки зрения лагранжевой модели аспектов реализации обоих компонентов в системе моделирования океан – лед.

Базовая модель океана комплекса совместного моделирования представлена численной моделью динамики океана ИВМИО [18]. Модель относится к классу 3D PEM – 3-Dimensional Primitive Equation Model. В ее основе лежит классическая система уравнений Рейнольдса в приближениях Буссинеска, гидростатики и несжимаемой жидкости. Свободная граница раздела атмосфера – океан описывается нелинейным кинематическим условием с явным описанием потоков воды, тепла, соли и импульса. На твердых границах задано условие проскальзывания и нулевого потока тепла и солености.

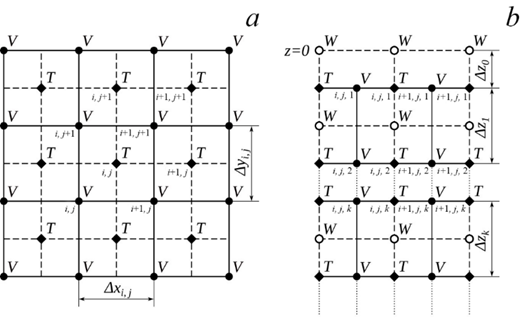
Р и с.  1. Расчетная сетка в модели ИВМИО: схема расположения узлов сетки в горизонтальной (а) и вертикальной (b) плоскости

F i g.  1. Calculation grid in the INMIO model: scheme of the arrangement of grid nodes in the horizontal (a) and vertical (b) planes

Исходные дифференциальные уравнения аппроксимируются методом конечных объемов на горизонтальной сетке типа B (рис. 1) с z-координатами по вертикали и в произвольной ортогональной системе координат по горизонтали (в данный момент поддерживаются декартовая, сферическая и трехполярная системы координат). Реализация численной модели адаптирована для параллельного выполнения на высокопроизводительных вычислительных системах методом двумерной декомпозиции модельной области.

В совместной модели океан – лед морской лед описывается с использованием модели  CICE5.1. Она определяет состояние льда и снега посредством функции распределения g (t, x, h), зависящей от времени, географических координат и толщины ледяного покрова. Основными прогностическими переменными являются сплоченность льда, средние по ячейке значения толщины льда и снега, внутренняя энергия льда и снега, соленость льда, температура и вектор скорости движения льда. Исходные уравнения термодинамики и транспорта льда аппроксимируются методом конечных разностей на сетке типа B в декартовой, полярной или трехполярной системе координат на поверхности океана.

Совместная система моделирования океан – лед реализована при помощи компактной вычислительной платформы CMF3.0 [5]. Помимо централизованного и параллельного ввода-вывода, CMF3.0 позволяет объединять несколько моделей в единую систему моделирования геофизических процессов при помощи процедуры переинтерполяции физических полей на различные сетки участвующих в моделировании компонентов.

На основе приведенной выше информации можно сформулировать более детальные требования к реализации лагранжевой модели. Реализация должна поддерживать централизованный ввод-вывод с заданной дискретностью через процедуры CMF3.0. Поскольку формулировка задачи для системы океан – лед не предусматривает перенос частиц в атмосферу, достаточно реализовать поддержку лагранжева переноса в модели океана и обеспечить переинтерполяцию поля скорости и потенциал ледообразования/таяния из модели льда методами компактной вычислительной платформы. Наконец, так как модель ИВМИО определена в произвольной ортогональной системе координат, то модель Лагранжа должна поддерживать транспорт частиц в любой системе координат.

Учитывая эти требования, процедуру вычисления траекторий лагранжевых частиц в модели океана можно представить в виде двух базовых операций: интерполяции дискретного поля скорости в точку с произвольной координатой (координаты частицы) в определенной системе координат и интегрирования уравнения, описывающего траекторию движения частицы в заданном поле течений.

Модель переноса лагранжевых частиц. Как было представлено во введении, с практической точки зрения в масштабах океана интересно отслеживать транспорт не только водных масс, но и растворенных микроэлементов: радионуклидов, нутриентов, планктона, минералов и др. При такой формулировке недостаточно просто вычислить перемещение жидкой частицы под действием заданного поля скорости, так как в заданном объеме масса растворенного материала в общем случае не является постоянной по причине турбулентного перемешивания. Поскольку мелкомасштабные процессы сложно описать в рамках общей модели циркуляции океана, эффект перемешивания должен быть представлен непосредственно в лагранжевой модели в виде переноса частиц под действием диффузии [1]. Таким образом, лагражева модель будет предусматривать перенос жидкой частицы с фиксированными физическими свойствами в поле заданной скорости под воздействием турбулентного перемешивания. При этом концентрация растворенного материала может быть задана количеством частиц в объеме. Впервые такой подход был представлен в работе [20] и с тех пор является основным для моделирования транспорта растворенного вещества [1].

Поскольку процессы турбулентного перемешивания имеют случайную природу, а процессы транспорта жидкой частицы и диффузии полагаются линейно независимыми, то для построения модели лагранжева переноса можно использовать аппарат стохастических дифференциальных уравнений. В общем виде уравнение представлено следующей формулой (это стохастическое дифференциальное уравнение, являющееся частным случаем уравнения Ланжевена, в котором дополнительное слагаемое описывает случайные флуктуации частицы, вызванные турбулентными процессами [21]):

 – координаты частицы в заданном пространстве; Ax,t – вектор детерминированного силового поля, определяющего эволюцию xt; Bx,t – предопределенный тензор, характеризующий стохастическое воздействие на частицу (в данном случае турбулентность); Lt – случайный вектор, определяющий хаотичную природу этих воздействий (турбулентная диффузия), компоненты которого – независимые случайные величины с нулевым математическим ожиданием.

Перемещение частицы под воздействием турбулентной диффузии можно представить в виде марковского процесса (для прогнозирования последующей координаты частицы достаточно информации о ее положении на текущем шаге), в котором случайные флуктуации описываются процессом Виннера и являются функцией от нормально-распределенной случайной величины с нулевым математическим ожиданием и дисперсией – dt. В работах  [1] показана связь между уравнением (1) и адвективно-диффузионным уравнением через прямое уравнение Колмогорова (уравнение Фоккера – Планка). Тогда, согласно работе ⁶, уравнение переноса лагранжевых частиц вдоль трех координатных осей можно представить в виде

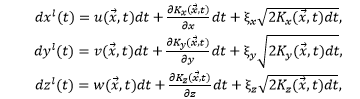                  (2)

где u, v, w – компоненты вектора скорости; K_x, K_y, K_z – коэффициенты турбулентной диффузии; ξ_x, ξ_y, ξ_z – независимые нормально-распределенные случайные величины с нулевым математическим ожиданием и единичной дисперсией. Стоит отметить, что второе слагаемое в правой части уравнений (2) введено искусственно для компенсации нереалистичного скопления частиц в областях с низкой диффузией ⁷ [22, 23], чтобы они физически корректно моделировали процессы турбулентной диффузии в рамках адвективно-диффузионного уравнения.

Мы внесли несколько модификаций в приведенную выше модель переноса лагранжевых частиц для ее оптимизации в рамках интересующих нас процессов. Во-первых, в масштабах вихреразрешающей модели океана эффектами горизонтальной турбулентной диффузии можно пренебречь, так как адвективные процессы в значительной мере преобладают над слабыми флуктуациями в горизонтальной плоскости ⁷. Во-вторых, в работах [24] отмечается, что слагаемое вертикальной турбулентной диффузии, отвечающее за случайные флуктуации, необходимо привести ко второму порядку точности, что позволит уточнить диффузионные процессы в придонном слое, где K_z стремится к нулю. В-третьих, на практике присутствие вещества, растворенного в заданном объеме, изменяет плотность раствора. В большинстве случаев этим можно пренебречь. Однако в некоторых задачах, особенно тех, которые предполагают длительные периоды моделирования или существенные концентрации пассивных трассеров, например при исследовании транспорта наносов ⁷, эффект изменения плавучести может оказаться значимым. Для этого в третье уравнение (2) введено дополнительное слагаемое, которое отвечает за перемещение частицы вдоль вертикальной оси с постоянной скоростью w^s и в первом приближении отражает этот процесс. Учитывая все описанные изменения, итоговая система уравнений переноса лагранжевых частиц будет иметь следующий вид:

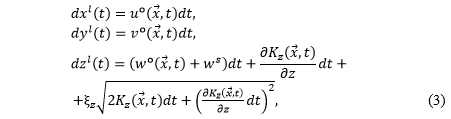
где u^o, v^o, w^o – составляющие вектора скорости течения жидкости в точке с заданными координатами.

Стоит особо отметить, что, согласно [1], на данный момент в открытом доступе отсутствуют реализации синхронных лагранжево-эйлеровых моделей океана, позволяющих вычислять траектории частиц на основе стохастического дифференциального уравнения (в данном случае явно учитывающего турбулентную диффузию). Нам также не удалось найти модели циркуляции океана, которые бы поддерживали транспорт лагранжевых частиц в такой формулировке. С этой точки зрения функционал переноса частиц в модели ИВМИО уникален.

Уравнения вида (3) имеют смысл только для переноса частиц в жидкой среде океана, где турбулентная диффузия вызвана мезомасштабными вихревыми процессами. Если же частица оказывается захваченной ледовым покровом, турбулентное перемешивание, очевидно, отсутствует. В этом случае частицы перемещаются вдоль вектора скорости движения льда. Такое движение описывается простым уравнением лагранжева транспорта

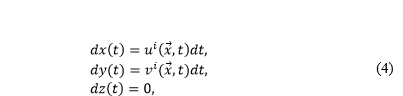
где uⁱ, vⁱ – горизонтальные составляющие вектора скорости льда. Поскольку в нашей модели не рассматриваются процессы переноса частиц за пределы поверхности океана, вертикальным перемещением частиц в ледяном покрове можно пренебречь. При этом момент перехода частиц в замороженное состояние и обратно можно оценить при помощи вероятностного подхода на основе интенсивности процессов ледообразования и таяния.

Как было отмечено ранее, система моделирования океан – лед объединяет две модели под управлением компактной вычислительной платформы CMF3.0. Это позволяет каждой из них получать необходимую информацию друг от друга с заданной дискретностью. В рамках лагранжева переноса в двухфазной среде нас интересует поле скорости льда, а также потенциала ледообразования и таяния. Первая величина, очевидно, будет напрямую использоваться в уравнениях (4) для перемещения частиц. Вторая величина – потенциал ледообразования и таяния – определяет в модели льда процедуры формирования замерзших структур в приповерхностном слое океана. Так, если она принимает положительные значения, это означает, что температура воды опустилась ниже температуры замерзания, что приводит к образованию льда, пропорциональному величине потенциала, и последующему накоплению льдинок на поверхности с постепенным образованием ледяного покрова. При отрицательных значениях потенциала происходит процесс таяния. В безразмерном виде описанная величина позволяет приближенно оценить вероятность замерзания или оттаивания лагранжевой частицы, если она оказалась в приповерхностном слое океана:

где T^o – температура жидкости в точке с текущими координатами лагранжевой частицы; Tf – температура ледообразования в этой точке. Формула (5) задает функцию вероятности события замерзания частицы, если она оказалась в приповерхностном слое при T^o < Tf, а также функцию вероятности оттаивания частицы, если она уже была заморожена при T^o ≥ Tf.

Таким образом, общую модель лагранжева переноса в квазидвухфазной среде океан – лед можно представить следующим образом:

1. Если частица находится в замерзшем состоянии, то ее перемещение описывается уравнениями (4), а вероятность оттаивания – функцией (5) при T^o ≥ Tf.

2. В противном случае частица перемещается свободно в жидкой среде согласно уравнениям (3) и может подвергнуться заморозке с вероятностью (5) в том случае, если она находится в приповерхностном слое жидкости (в самой верхней ячейке численной модели) при T^o < Tf.

Такой подход позволяет реализовать модель без необходимости передачи информации о частице в модель льда. Это существенно экономит вычислительные ресурсы, а также упрощает код программы.

Для численного интегрирования уравнений переноса лагранжевых частиц, как правило, применяется либо явная схема Эйлера, либо схемы Рунге – Кутты [1] разных порядков точности. При автономной реализации совместной модели, когда временна́я дискретизация поля скорости достаточно большая, для увеличения точности воспроизведения траекторий частиц применяется высокий порядок аппроксимации по времени исходных уравнений (3) и (4). Здесь применяются, например, метод Хюна, схемы Рунге – Кутты четвертого порядка и выше ⁷ [1, 25].

В случае совместной модели требование высокого порядка схемы по времени становится не столь существенным и можно воспользоваться схемой Эйлера первого порядка точности. Изменять точность численного интегрирования исходных уравнений можно путем уменьшения шага по времени внутри численной реализации лагранжевой модели. Результаты тестовых численных экспериментов по переносу частиц в статичном круговом поле течений показывают, что независимо от схемы (Эйлера, Рунге – Кутта) шаг интегрирования по времени в модели лагранжева переноса должен быть заметно меньше, чем в модели океана, чтобы достичь приемлемой точности воспроизведения траекторий движения частицы по окружности [1]. Таким образом, разностная схема исходных уравнений переноса лагранжевых частиц в поле скорости совместной системы моделирования океан – лед будет выглядеть следующим образом:

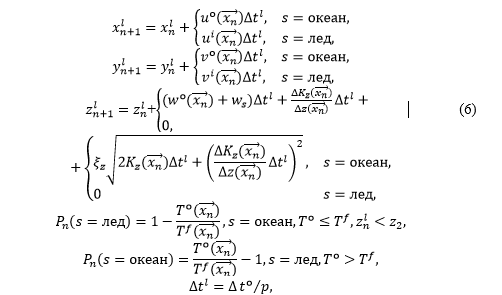
где xn=xnl,ynl,znl – координата лагранжевой частицы на n-м шаге интегрирования; uo=uoxn,voxn,woxn – скорость течения в точке с координатами частицы; ui=uixn,vixn,0 – скорость движения льда; Δt^l – шаг по времени в модели Лагранжа,; Δt^o – шаг по времени в модели океана; p – целое число, определяющее фактор уточнения порядка интегрирования лагранжевой модели по отношению к модели ИВМИО. По результатам тестовых расчетов при p ~ 10 решение достигает приемлемой точности.

Интерполяция в модели переноса лагранжевых частиц. Моделирование лагранжева переноса предполагает перемещение частиц в пространстве непрерывно заданных координат (6). То есть в произвольный момент времени координаты частиц могут не совпадать с координатами узлов расчетной области численной модели. Значит, для достижения большей точности необходимо доопределить дискретное поле скорости системы океан – лед внутри вычислительных ячеек. Как правило, это достигается интерполяционными методами различных порядков [1]. В рамках данной работы выбор был остановлен на линейной интерполяции, поскольку она наименее затратна с точки зрения вычислительных ресурсов и позволяет достичь приемлемой точности [25].

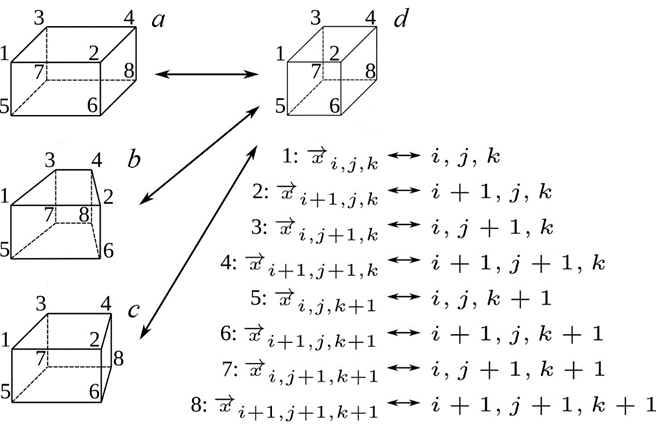
Р и с.  2. Отображение вычислительных ячеек в различных системах координат: декартовой (а), полярной (b), двуполярной (с), полулогической (d)

F i g.  2. Display of computational cells in different coordinate systems: Cartesian (a), polar (b), bipolar (c) and semi-logical (d) ones

Однако применение этого подхода сильно осложняется тем, что уравнения модели ИВМИО заданы в произвольной ортогональной системе координат по горизонтали. В такой конфигурации процедуры определения положения частицы на вычислительной сетке и интерполяция становятся нетривиальными. Одним из способов решить проблему, сохранив простоту формул линейной интерполяции, является переход к рассмотрению уравнений переноса частиц в логическом (вычислительном) пространстве (рис. 2) [25].

Это пространство представляет собой декартову систему координат, которая естественным образом вводится при реализации большинства численных моделей и описывается индексами узлов расчетной сетки. Переход к логическим координатам имеет смысл только в горизонтальной плоскости, так как в модели ИВМИО введена z-координата по вертикали. Тогда координаты точек в новом полулогическом пространстве C можно представить как ξ=ξ,η,z, где ξ = i + α, η = j + β, а функция его отображения в физическое пространство P будет иметь вид

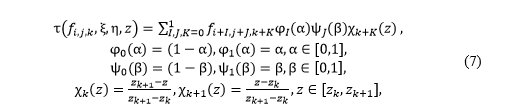
где i, j, k – индекс ячейки расчетной области; α, β – вещественное смещение точки в логическом пространстве относительно индекса ячейки; f_{i, j, k} – функция, определяющая значение величины в узлах сетки физического пространства; φ, ψ, χ – базовые функции отображения. Если функция f задает векторы с координатами узлов ячейки в физическом пространстве, выражение (7) можно использовать для вычисления координат точки в физическом пространстве по заданным координатам в полулогическом пространстве. Если же функция f задает векторы скорости, выражение (7) определяет трилинейную интерполяцию скорости внутрь заданной ячейки (см. рис. 1).

     Однако при переходе в полулогическое пространство вектор движения частиц должен быть перемасштабирован в соответствии с деформацией пространства вдоль соответствующих координатных осей. Согласно [25], это можно сделать при помощи следующего преобразования в рамках отображения, введенного ранее:

где u=u,v,w – вектор скорости в физическом пространстве; ω=u,v,w – вектор скорости в полулогическом пространстве; J – матрица Якоби, определяющая деформацию пространства при переходе из физической в полулогическую систему координат.

     На дискретной сетке матрицу J можно вычислить при помощи конечных разностей. Однако, как показано в работе [25], для достижения наибольшей точности это необходимо сделать для всех узлов вычислительной ячейки, применяя восходящие и нисходящие конечные разности. Очевидно, этого можно достичь, используя функцию отображения τx,ξ,η,z (7), которая определяет переход от полулогических координат в физические. При этом легко показать, что в третьем столбце и в третьей строке матрицы Якоби все элементы, кроме последнего, будут равны нулю, так как заданное отображение не затрагивает ось OZ. Тогда для каждой вычислительной ячейки (i, j, k) матрица примет вид

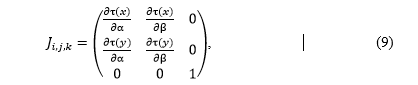
где частные производные вычисляются тривиальными образом для функции τx,ξ,η,z  вида (7).

     Особо следует отметить, что уравнения (6) инвариантны для заданного выше отображения, поскольку измерение OZ остается неизменным. Для получения координат лагранжевой частицы в следующий момент времени достаточно масштабировать вектор скорости в узловых точках ячейки по формулам (8) и (9), затем интерполировать ее в точку с координатами частицы при помощи (7) и напрямую использовать полулогические координаты и полученный вектор скорости в уравнениях (6).

Результаты и обсуждение

Тестовые расчеты переноса частиц в поле статического вихря. Поскольку различные аспекты математической модели, приведенной выше, неоднократно проверялись, например в работах ^7, 8 [1, 24], основная задача данных тестовых расчетов – продемонстрировать корректность реализации модели лагранжева переноса и методов ее интегрирования на сетках, поддерживаемых моделью океана ИВМИО, в декартовой и геосферической/трехполярной системе координат.

     Программная модель ИВМИО была сконфигурирована для расчета области в географическом прямоугольнике 53°–59° в. д., 68°–72° с. ш. Для тестирования переноса частиц введено искусственное поле скорости, представляющее собой статический вихрь с центром в середине области и периодом вращения ~ 10 дней (угловая скорость W = 7,27·10⁻⁶ рад/c). В случае с декартовой системой координат поле линейной скорости было представлено в географических единицах (град/с). В случае же со сферической системой координат размерность поля скорости соответствовала метрической системе мер (м/с) для вихря с заданной угловой скоростью и центром на поверхности земного шара с географическими координатами, приведенными ранее. Модель аппроксимировалась на сетку 60 × 40 вычислительных ячеек, соответствующих разрешению 0,1° расчетной области. Шаг интегрирования в модели океана задавался равным Δt^o = 6¢. Временна́я дискретизация лагранжевой модели варьировалась для получения наиболее точных траекторий частиц. Очевидно, для заданного поля скорости траектории должны представлять собой концентрические линии тока. Расчет проводился в параллельном режиме на шести вычислительных ядрах. На рис. 3 представлены результаты тестового расчета переноса лагранжевых частиц на сетке в декартовой системе координат.

     Как и следовало ожидать, частицы двигаются синхронно друг с другом по кругу вдоль линий тока, заданного в расчетной области вихревого поля скорости. Видно, что процесс перехода частиц между ячейками и вычислительными доменами (толстые линии на рис. 3) не приводит к искажению их траекторий, а координаты частиц соответствуют их движению в вихре с периодом ~ 10 дней. Представленные на рис. 3 траектории были получены при p = 5 в выражениях (6).

     В следующем тестовом численном эксперименте частицы двигались на сетке в географической системе координат.

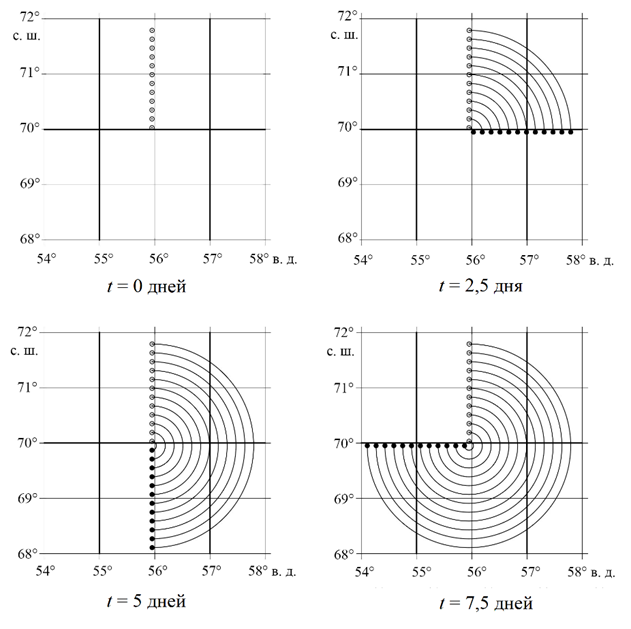
Р и с.  3. Траектории частиц, двигающихся в поле статического вихря, на сетке в декартовой системе координат

F i g.  3. Trajectories of particles moving in the static vortex field on a grid in the Cartesian coordinate system

На рис. 4 представлены результаты расчетов в различные моменты времени моделирования. Как и в предыдущем случае, частицы двигаются синхронно друг с другом вдоль линий тока вихревого поля скорости. Траектории по-прежнему имеют круговую форму, но только в метрическом представлении пространства. В географических координатах они уже не являются таковыми, а представляют собой вытянутые вдоль широтной оси эллипсообразные кривые. Как и ранее, представленные на рис. 4 траектории были получены при p = 5 в выражениях (6).

С точки зрения получения более точных траекторий движения лагранжевых частиц особый интерес представляет их переход между двумя вычислительными ячейками и, как частный случай, переход между подобластями двумерной декомпозиции расчетной области модели океана. В первом случае интерес связан с особенностями моделирования в полулогическом пространстве, в котором поле скорости на границе уже не является непрерывной функцией (формулы (7) и (8)). Поэтому для получения максимальной точности скорость и путь частицы должны быть пересчитаны при переходе через границу ячейки (при моделировании в физическом пространстве это условие тоже актуально, но, очевидно, по другой причине). В нашей реализации это условие выполняется лишь частично путем задания малого по сравнению с моделью океана шага интегрирования по времени (6). С другой стороны, «бесшовный» перенос частиц между двумя вычислительными доменами означал бы корректность реализации алгоритма параллельного расчета лагранжевой модели.

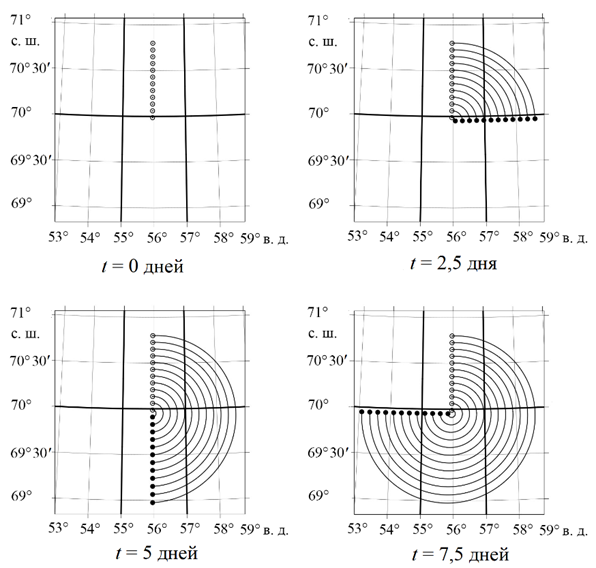
Р и с.  4. Траектории частиц, двигающихся в поле статического вихря, на сетке в географической системе координат

F i g.  4. Trajectories of particles moving in the static vortex field on a grid in the geographic coordinate system

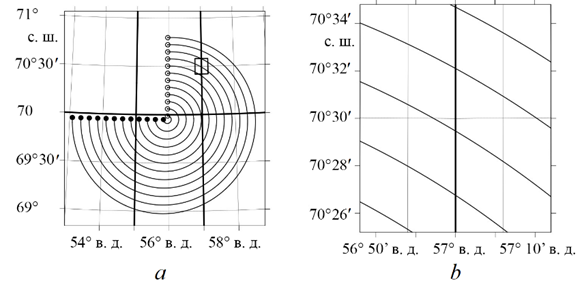
Р и с.  5. Траектории частиц в тестовом эксперименте на сетке в географической системе координат (прямоугольником выделена область на границе вычислительных ячеек и расчетной области) (a), увеличенное изображение выделенной области (b)

F i g.  5. Particle trajectories in the test experiment on a grid in the geographic coordinate system (rectangle highlights the region on the boundary of computational cells and calculation domain) (a), enlarged image of the highlighted area (b)

     На рис. 5 для примера показаны траектории частиц, пересекающие границу двух расчетных подобластей и нескольких вычислительных ячеек. Как видно, траектории не претерпевают видимых разрывов. Это свидетельствует, во-первых, о достижении достаточной точности для заданного Δt^l (p = 5 в формулах (6)) и, во-вторых, о корректности межпроцессорного обмена частицами в параллельной модели лагранжева переноса.

Тестовый расчет переноса частиц в совместной модели океан – лед. Основная задача данного тестового расчета – продемонстрировать корректность реализации лагранжевой модели, описанной выше, в системе моделирования океан – лед, представленной моделями океана ИВМИО и моделью термодинамики льда CICE5.1. Конфигурация модели океана для СЛО описана в работе [6], однако в качестве модельной области было выбрано море Лаптевых (71°–91° с. ш., 120°–140° в. д.), акватория которого почти круглый год покрыта морским льдом. Модельная топография интерполировалась на основе данных ЕТОРО5 . Атмосферное воздействие определялось нормальным годовым циклом в соответствии с условиями международного эксперимента CORE-I [26]. Расчетная сетка по горизонтали в модели океана и модели льда определялась в сферической системе координат размером 160 × 80 узлов по горизонтали и 49 горизонтов по вертикали. Таким образом, совместная модель океан – лед работала с разрешением 0,125°. Шаг интегрирования в моделях океана и льда задан одинаковым Δt^o = Δtⁱ = 5¢. При этом в лагранжевой модели он составлял Δt^l = 1¢. Координаты частиц сохранялись с той же дискретностью. Данные физических полей, среди прочего включающие скорость движения льда, в системе океан – лед синхронизировались каждые 10¢. Установочное время моделирования системы океан – лед составляло 1 год, по истечении которого синхронно запускалась лагранжева модель еще на два модельных месяца для 10⁴ частиц, расположенных в области с координатами 76° с. ш. и 130° в. д. в приповерхностном слое. Расчет запускался в параллельном режиме на 16 вычислительных ядрах для модели океана.

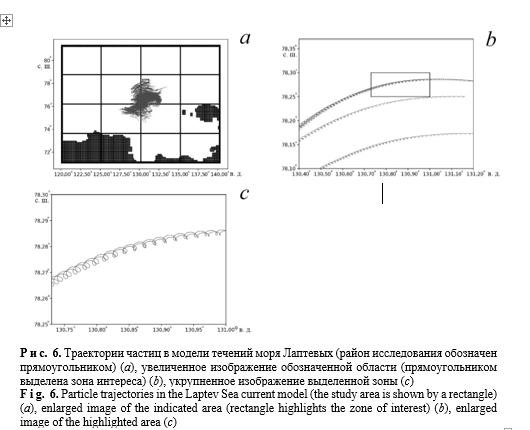
     На рис. 6, a показаны горизонтальные траектории частиц через два месяца совместного численного интегрирования модели динамики океан – лед и модели лагранжева переноса. Как видно, под воздействием внутренних течений частицы двигаются по различным траекториям, что и следовало ожидать от модели, учитывающей эффекты турбулентного перемешивания. На рис. 6, b в увеличенном масштабе показаны траектории нескольких частиц, которые попали в прямоугольник, обозначенный на рис. 6, a. Форма траекторий отражает два основных динамических процесса: квазиоднородный в выделенной области течения и круговые движения, которые соответствуют инерционным колебаниям в поле течений. Более детальное увеличение (рис. 6, c) показывает синхронное перемещение двух близких частиц в горизонтальной плоскости.

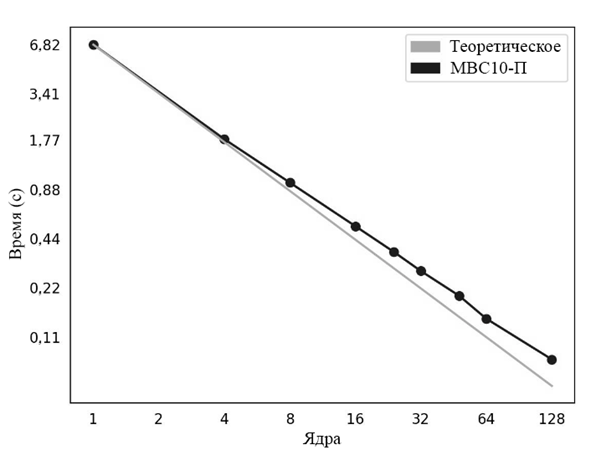
Р и с.  7. График зависимости времени одного шага лагранжевой модели от количества ядер в эксперименте с равномерным распределением частиц в моделируемой области

F i g.  7. Graph of the dependence of one step duration in the Lagrangian model upon the core number in the experiment with uniform particle distribution in the simulated region

     С целью оценки масштабируемости программной реализации модели лагранжева переноса была проведена серия численных экспериментов для 10⁶ частиц, равномерно распределенных по поверхности моделируемого в указанном численном эксперименте пространства (рис. 7). Как видно, функция зависимости времени, затраченного на вычисление одного шага в модели лагранжева переноса, от количества вычислительных ядер близка к линейной, что свидетельствует о хорошей масштабируемости реализованного параллельного алгоритма расчета лагранжева переноса. Однако стоит отметить, что это справедливо только для случая равномерно распределенных по расчетной области частиц, что в реальных расчетах встречается редко. Под действием течений концентрация частиц в вычислительных доменах не является постоянной величиной, а будет эволюционировать. Потому общее время, затраченное на каждый шаг интегрирования в модели лагранжева переноса, будет определяться доменом с максимальным количеством частиц.

Заключение

     В работе представлена модель переноса лагранжевых частиц в квазидвухфазной среде океан – лед, учитывающая вертикальное турбулентное перемешивание и реализованная в модели общей циркуляции океана ИВМИО для произвольно заданной по горизонтали системы координат. Поддержка двухфазности и турбулентной диффузии является уникальным свойством среди существующих на данный момент моделей динамики океана. Такой инструмент особенно актуален в связи с активным освоением Арктического региона.

     Реализация модели поддерживает параллельный расчет транспорта большого количества частиц (до 10⁶) в рамках двухмерной декомпозиции расчетной области. При этом показано, что для равномерно распределенной концентрации лагранжевых частиц алгоритм имеет масштабируемость, близкую к линейной. Расчет траекторий частиц производится на вычислительных ядрах модели океана, что обусловливает указанное ограничение на количество частиц. В ином случае учет более 10⁶ частиц, сосредоточенных в одном расчетном домене, неизбежно приведет к разбалансировке вычислительной нагрузки, что негативно скажется на производительности модели. Впрочем, худший вариант такого события маловероятен и характерен лишь для начального момента времени, когда по условиям поставленной задачи частицы, как правило, сосредотачиваются в одном или нескольких расчетных доменах. В процессе эволюции численного решения частицы будут неизбежно перенесены в различные участки расчетной области, а процессы турбулентного перемешивания лишь поспособствуют этому.

     Разработанный алгоритм межпроцессорного обмена, обеспечивающий передачу данных о частицах, покинувших подобласть одного вычислительного ядра и перешедших в подобласть другого, гарантирует возможность перемещения частиц во всей расчетной области модели океана. При этом на примере тестового расчета показано, что для достижения относительной гладкости траекторий при пересечении границы ячейки вполне достаточно задать шаг интегрирования в пять раз меньший, чем шаг по времени в модели океана.

1. Lagrangian ocean analysis: Fundamentals and practices / E. van Sebille [et al.] // Ocean Model-ling. 2018. Vol. 121. P. 49–75. https://doi.org/10.1016/j.ocemod.2017.11.008

2. Хвостова М. С. Экологические проблемы эксплуатации плавучей атомной теплоэлектро-станции в Арктическом регионе // Российская Арктика. 2018. № 1. С. 11–29. EDN XVMEXR.

3. Прогноз и оценка радиоэкологических последствий гипотетической аварии на затонув-шей в Баренцевом море атомной подводной лодке Б-159 / С. В. Антипов [и др.] // Атом-ная энергия. 2015. Т. 119, № 2. С. 106–113. EDN UEKIWZ.

4. Ушаков К. В., Ибраев Р. А., Калмыков В. В. Воспроизведение климата Мирового океана с помощью массивно-параллельной численной модели // Известия Российской академии наук. Физика атмосферы и океана. 2015. Т. 51, № 4. С. 416–436. EDN SCWLAR. https://doi.org/10.7868/S0002351515040136

5. Compact Modeling Framework v3.0 for high-resolution global ocean–ice–atmosphere models / V. V. Kalmykov [et al.] // Geoscientific Model Development. 2018. Vol. 11. P. 3983–3997. https://doi.org/10.5194/gmd-11-3983-2018

6. Сезонная изменчивость циркуляции вод и морского льда в Северном Ледовитом океане в модели высокого разрешения / Л. Ю. Кальницкий [и др.] // Известия Российской ака-демии наук. Физика атмосферы и океана. 2020. Т. 56, № 5. С. 598–610. EDN QNBBHV. https://doi.org/10.31857/S0002351520050065

7. Кулаков М. Ю., Макштас А. П., Шутилин С. В. AARI-IOCM – совместная модель цир-куляции вод и льдов Северного Ледовитого океана // Проблемы Арктики и Антарктики. 2012. № 2 (92). С. 6–18. EDN OYZSIF.

8. Campin J.-M., Marshall J., Ferreira D. Sea ice-ocean coupling using a rescaled vertical coor-dinate z* // Ocean Modelling. 2008. Vol. 24. P. 1–14. https://doi.org/10.1016/j.ocemod.2008.05.005

9. Design and development of the SLAV-INMIO-CICE coupled model for seasonal prediction and climate research / R. Yu. Fadeev [et al.] // Russian Journal of Numerical Analysis and Mathematical Modelling. 2018. Vol. 33, iss. 6. P. 333–340. https://doi.org/10.1515/rnam-2018-0028

10. Development of a Coupled Ocean–Atmosphere–Wave–Sediment Transport (COAWST) Mod-eling System / J. C. Warner [et al.] // Ocean Modelling. 2010. Vol. 35, iss. 3. P. 230–244. https://doi.org/10.1016/j.ocemod.2010.07.010

11. Döös K., Jönsson B., Kjellsson J. Evaluation of oceanic and atmospheric trajectory schemes in the TRACMASS trajectory model v6.0 // Geoscientific Model Development. 2017. Vol. 10, iss. 4. P. 1733–1749. https://doi.org/10.5194/gmd-10-1733-2017

12. Blanke B., Raynaud S. Kinematics of the Pacific Equatorial Undercurrent: An Eulerian and La-grangian Approach from GCM Results // Journal of Physical Oceanography. 1997. Vol. 27, iss. 6. P. 1038–1053. https://doi.org/10.1175/1520-0485(1997)027<1038:KOTPEU>2.0.CO;2

13. Connectivity Modeling System: A probabilistic modeling tool for the multiscale tracking of biotic and abiotic variability in the ocean / C. B. Paris [et al.] // Environmental Modelling & Software. 2013. Vol. 42. P. 47–54. https://doi.org/10.1016/j.envsoft.2012.12.006

14. Golubeva E., Gradova M. Numerical Study of the Riverine Microplastic Distribution in the Arctic Ocean // Water. 2024. Vol. 16, iss. 3. 441. https://doi.org/10.3390/w16030441

15. Bleck R. An oceanic general circulation model framed in hybrid isopycnic-Cartesian coordinates // Ocean Modelling. 2002. Vol. 4, iss. 1. P. 55–88. https://doi.org/10.1016/S1463-5003(01)00012-9

16. Shchepetkin A. F., McWilliams J. C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model // Ocean Modelling. 2005. Vol. 9, iss. 4. P. 347–404. https://doi.org/10.1016/j.ocemod.2004.08.002

17. A finite-volume, incompressible Navier Stokes model for studies of the ocean on parallel com-puters / J. Marshall [et al.] // Journal of Geophysical Research: Oceans. 1997. Vol. 102, iss. C3. P. 5753–5766. https://doi.org/10.1029/96JC02775

18. Ибраев Р. А., Хабеев Р. Н., Ушаков К. В. Вихреразрешающая 1/10º модель Мирового океана // Известия Российской академии наук. Физика атмосферы и океана. 2012. Т. 48, № 1. С. 45–55. EDN OOWHJD.

19. Калмыков В. В., Ибраев Р. А. Программный комплекс совместного моделирования си-стемы океан–лед–атмосфера–почва на массивно-параллельных компьютерах // Вычисли-тельные методы и программирование. 2013. T. 14, № 3. С. 88–95. EDN ROWAVZ.

20. Maier-Reimer E., Sündermann J. On tracer methods in computational hydrodynamics // Engi-neering Applications of Computational Hydroulics / Eds. M. B. Abbot, J. A. Cunge. Boston, London, Melbourne : Pitman Advanced Publishing Program, 1982. Vol. 1. P. 198–217.

21. Gardiner C. W. Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sci-ences / Ed. H. Haken. Berlin : Springer-Verlag, 1985. 439 p. https://doi.org/10.1007/978-3-662-02452-2

22. Hunter J. R., Craig P. D., Philips H. E. On the use of random walk models with spatially vari-able diffusivity // Journal of Computational Physics. 1993. Vol. 106, iss. 2. P. 366–376. https://doi.org/10.1016/S0021-9991(83)71114-9

23. Visser A. W. Using random walk models to simulate the vertical distribution of particles in a turbulent water column // Marine Ecology – Progress Series. 1997. Vol. 158. P. 275–281. https://doi.org/10.3354/meps158275

24. Sunarko, Su’ud Z. Lagrangian Particle Method for Local Scale Dispersion Modeling // Journal of Physics: Conference Series. 2016. Vol. 739. 012122. https://doi.org/10.1088/1742-6596/739/1/012122

25. Particle Tracing Algorithms for 3D Curvilinear Grids / A. Sadarjoen [et al.] // Scientific Vizual-ization. Overviews. Methodologies. Techniques / Eds. G. Nielson, H. Müller, H. Hagen. Delft University of Technology, 1994. P. 299–323.

26. Coordinated Ocean-ice Reference Experiments (COREs) / S. M. Griffies [et al.] // Ocean Mod-elling. 2009. Vol. 26, iss. 1–2. P. 1–46. https://doi.org/10.1016/j.ocemod.2008.08.007