Введение

Необходимость мониторинга короткопериодной и субмезомасштабной изменчивости характеристик гидрологических полей океана с целью определения географических особенностей их вклада в диссипативные процессы на шельфе различных акваторий представляется одной из важных текущих задач физики океана [1]. Основная сложность при решении данной задачи заключается в необходимости получения высокоразрешающих одновременно по пространству и времени измерений [2]. Подобная задача для локальных акваторий может быть решена, например, при помощи разнесенных в пространстве кластеров измерителей температуры в виде заякоренных цепочек (термокос) [3] или интегральных датчиков [4]. Однако постановка и снятие заякоренных станций сопряжены со значительными трудностями и рисками. Можно также использовать группы термокос (термолиний), опускаемых с борта судна [5] или буксируемых за ним [6].

Очевидно, что подобные подходы применимы в любых точках Мирового океана, однако с учетом значительной трудоемкости и стоимости подобных работ возникают естественные вопросы об экономической эффективности, выборе районов и сроков наблюдений. Ответы на эти вопросы подводят к идее применения автономных поверхностных дрейфующих буев типа SVP. Их успешное использование в таких программах, как GDP (Global Drifting Program) , UpTempO , подтвердило высокую эффективность при изучении деятельного слоя океана [7]. Поэтому термопрофилирующие дрейфующие буи (SVP‑BTC60/GPS/ice), использовавшиеся для исследования Арктического региона в программе UpTempO, опыт изготовления которых есть у отечественных производителей [8], могут рассматриваться как прототип для создания недорогой и мобильной системы мониторинга.

Усовершенствование буев данного типа и объединение нескольких в единый измерительный кластер позволили [9, 10] разработать прототип системы мониторинга короткопериодной изменчивости температуры деятельного слоя Мирового океана. Она, в частности, позволяет вести наблюдение за характеристиками поля короткопериодных внутренних волн (КВВ) в любой точке Мирового океана, оперативно передавать и обрабатывать получаемые данные. Используемые буйковые средства наблюдений адаптированы для круглогодичного применения в Арктике. Комплексная информационная система обеспечивает сбор данных измерений, их прохождение в каналах связи буй – пользователь, обработку и представление данных в масштабе времени, близком к реальному, что позволяет определять амплитуды, периоды, скорость и направление распространения короткопериодных внутренних волн по разнице во времени между прибытиями пакета волн к различным буям массива.

В работе [11] отмечается, что аналогичные системы использовались в 1980–1990‑е гг., однако их техническое несовершенство привело к отказу от методики. Системы нового поколения начинают активно применяться для регистрации пространственных характеристик внутренних волн в экспедиционной практике. Поэтому методическая база их использования только начинает формироваться. Требуется практически с нуля разработать специализированное программное обеспечение для обработки данных, получаемых от конкретной буйковой системы.

Цель работы – представить краткое техническое описание созданного массива дрейфующих буев, принципов функционирования их измерительной системы, описать алгоритм анализа характеристик внутренних волн и примеры его применения.

Материалы и методы

Используемый массив дрейфующих буев. Для регистрации характеристик КВВ использовались гидрофизическая измерительная система «Волна-ДС-01» (дрейфующая система) фирмы «Марлин-Юг» (Россия), состоящая из автономных, свободно дрейфующих поверхностных термопрофилирующих буев «Волна-ДБ-01» (дрейфующий буй) в количестве не менее трех единиц (количество может быть увеличено в несколько раз), и станции автоматического приема информации с дрейфующих буев «Волна‑ПС-01» (приемная станция). На рис. 1, а представлена схема гидрофизической измерительной системы «Волна-ДС-01».

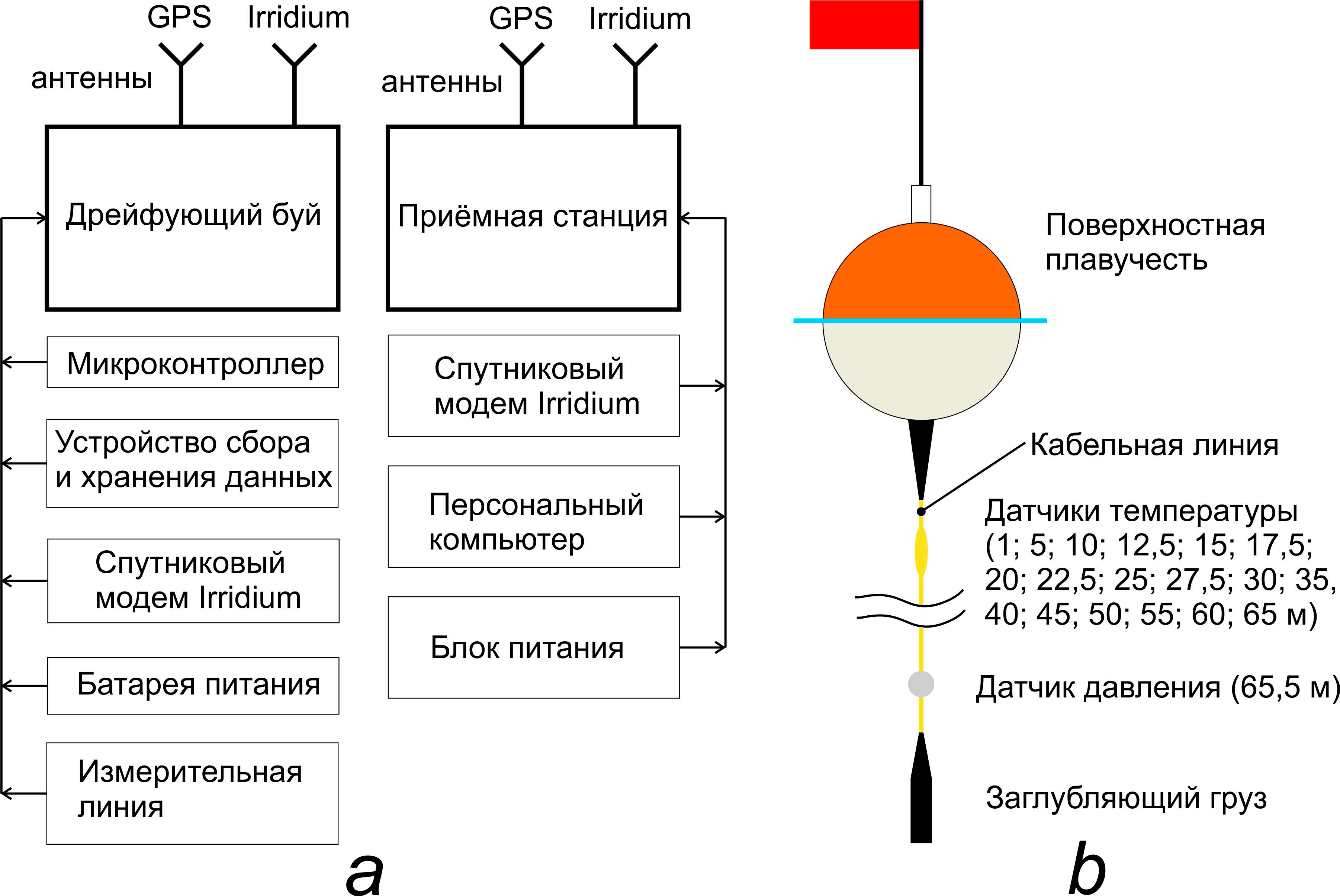
Р и с.  1. Гидрофизическая измерительная система «Волна-ДС-01»: a – схема составных частей (дрейфующий буй «Волна-ДБ-01» и приемная станция «Волна-ПС-01»); b – принципиальная схема дрейфующего буя

F i g.  1. Hydrophysical measuring system “Volna-DS-01”: a – diagram of the components (drifting buoy “Volna-DB-01” and receiving station “Volna-PS-01”); b – schematic diagram of a drifting buoy

Каждый дрейфующий буй (рис. 1, b) состоит из плавучего корпуса и измерительной линии. Корпус выполнен из двух поликарбонатных полусфер, герметично соединенных фланцевым креплением. В верхней части корпуса размещен герметичный отсек с интерфейсом USB A для подключения флеш-накопителя. На корпусе устанавливается флагшток с красным сигнальным флагом, оборудованный линем для облегчения операций постановки и выборки дрейфующего буя.

В герметичном пространстве корпуса размещены элементы электропитания, обеспечивающие продолжительность непрерывной работы не менее 1200 ч, контроллер с системой реального времени, модуль ГНСС ГЛОНАСС/GPS с антенной, модем спутниковой системы Iridium с антенной. Модуль ГНСС обеспечивает определение координат каждого дрейфующего буя и синхронизацию времени измерений. Спутниковый модем обеспечивает оперативную передачу географических координат каждого дрейфующего буя с дискретностью 10 мин. Синхронно с географическими координатами передаются данные измерений профиля температуры и гидростатического давления, параметры источника питания буя и дополнительная диагностическая информация. Плавучий корпус оборудован магнитным выключателем питания и световыми индикаторами режима работы измерительной системы и статуса спутниковой передачи данных.

Измерительная линия представляет собой кабель типа «витая пара» с несущим тросом. В кабель герметично интегрированы 18 цифровых датчиков температуры и датчик гидростатического давления, показания которого используются для определения фактических горизонтов датчиков температуры при отклонениях измерительной линии от вертикали. Номинальные горизонты расположения датчиков указаны на рис. 1. Конструкция корпусов датчиков температуры обеспечивает их хорошую омываемость окружающей водой для снижения постоянной времени. На нижнем конце измерительной линии расположен заглубляющий груз.

Приемная станция «Волна-ПС-01» состоит из блока приема информации, антенн спутниковой системы Iridium и ГНСС и персонального компьютера (ноутбука) со специализированным программным обеспечением (ПО). В блоке приема информации установлены модем спутниковой системы Iridium, контроллер и измеритель атмосферного давления, предназначенный для коррекции показаний датчиков гидростатического давления на буях. Антенна ГНСС имеет в составе GPS-приемник типа BU-353s4/BR-355s4 (GlobalSat). ПО отображает принятую станцией информацию в графическом (распределения температур по глубине, карта дрейфа) и текстовом (координаты буев, координаты и скорость движения станции) форматах. Взаимное расположение приемной станции и дрейфующих буев может быть произвольным, что позволяет производить мониторинг состояния системы как с судна, так и с берегового поста.

Информация о характеристиках датчиков, применяемых в дрейфующей системе, представлена в таблице. Минимально возможная дискретность измерений составляет 10 с.

Технические и метрологические характеристики датчиков дрейфующей системы

Technical and metrological characteristics of the drifting system sensors

Примеры применения системы. На рис. 2 отмечены места применения гидрофизической измерительной системы «Волна-ДС 01».

Испытания гидрофизической измерительной системы проводились в Кондопожской губе и заливе Большое Онего Онежского озера в июне 2022 г. в рамках экспедиции Карельского научного центра на НИС «Эколог» (точка 1 на рис. 2). Выбор Онежского озера в качестве испытательного полигона обусловлен следующими факторами: минимизацией рисков нарушения работоспособности или потери оборудования, возможностью применения дрейфующей системы для регистрации характеристик КВВ в большом стратифицированном водоеме.

Морские измерения с применением дрейфующей системы были выполнены в июле 2023 и 2024 гг. в Карском море в рамках экспедиций «Плавучего университета» на НИС «Дальние Зеленцы» и «Профессор Молчанов». Постановка дрейфующей системы производилась в проливе Карские Ворота (точки 2 и 3 на рис. 2), над Новоземельским желобом (точка 4 на рис. 2) и около м. Желания (точка 5 на рис. 2).

В Онежском озере было выполнено шесть измерений суммарной продолжительностью 46 ч. Продолжительность каждого измерения составляла от 3 до 10 ч. Пример карты дрейфа буев приведен на врезке рис. 2. В Карском море было выполнено пять измерений продолжительностью от 6 до 12 ч и общей длительностью 37 ч.

Дрейфующие буи ставились и снимались при волнении моря до трех баллов с рабочего катера вручную, чтобы избежать повреждения плавучих корпусов. В ходе измерений каждым дрейфующим буем была собрана информация о вертикальном распределении температуры в слое от 1 до 65 м, о координатах дрейфа данного буя, которая была дополнена результатами контрольных (фоновых) измерений CTD-зондами CastAway (США), CTD48M (Германия), SBE19plus V2 (США) с судов.

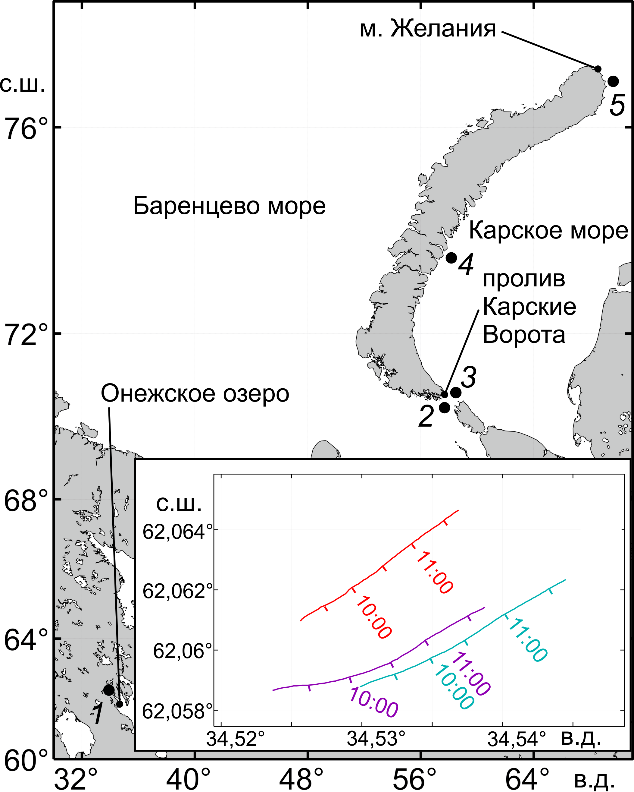
Р и с.  2. Карта применения гидрофизической измерительной системы (1 – Онежское озеро; 2, 3 – Карские Ворота; 4 – Новоземельский желоб; 5 – м. Желания); на врезке – карта дрейфа буев Б₁–Б₃ (1–3 – серийный номер изготовителя) в Онежском озере 16 июня 2022 г. (красная линия – буй Б₁, фиолетовая – буй Б₂, бирюзовая – буй Б₃)

F i g.  2. Map of application of the hydrophysical measuring system (1 – Lake Onega; 2, 3 – Kara Gate Strait; 4 – Novozemelsky trench; 5 – Zhelaniya Cape); inset – map of the buoys Б₁–Б₃ drifts (1–3 are the manufacturer serial numbers) in Lake Onega on June 16, 2022 (red line shows buoy Б₁, purple line – buoy Б₂ and turquoise one – buoy Б₃)

В работе будут рассмотрены в качестве примера результаты регистрации характеристик КВВ в Онежском озере в июне 2022 г. (рис. 2, врезка) и в восточной части пролива Карские Ворота в июле 2023 г.

Методика оценки характеристик КВВ по данным дрейфующей системы. Для регистрации скорости и направления распространения КВВ необходимы одновременные измерения как минимум в трех точках, разнесенных по пространству. Эти характеристики КВВ обычно оцениваются по разнице во времени между прибытиями волновых пакетов к измерителям, расположенным в вершинах треугольника [6]. То есть от точности определения времени задержки прибытия пакета волн зависит точность оценок скорости и направления распространения.

Существуют различные методы оценки времени задержки. Так, в работах [5, 11, 12, 13] время задержки оценивается визуально непосредственно по записям колебаний температуры. Данный метод эффективно работает при регистрации хорошо различимых солитоноподобных волн. При наличии на записях последовательных пакетов волн сложной структуры применение данного метода может быть затруднено. Описан также метод оценки времени задержки по максимумам кросскорреляционной функции [4, 6]. Данный метод применим при расположении измерителей в вершинах треугольника с длиной стороны, много меньшей длины регистрируемых волн, что не всегда удобно для реализации. Возможно определение времени задержки по максимумам интегральной температуры [14] или максимумам скорости изменения температуры на некотором горизонте [3]. Однако применение этих методов описано в основном для волн большой амплитуды и солитоноподобных волн.

В данной работе для оценки времени задержки прибытия пакета волн применялась оценка скользящей дисперсии [15] глубины залегания изотерм. Скользящая дисперсия успешно применяется для оценки флуктуаций различных параметров ионосферы [16], геохимических параметров [17], а также скорости течений в океане [9, 18]. Поскольку скользящая дисперсия отражает локальные изменения свойств временно́го ряда, максимумы скользящей дисперсии хорошо соответствуют как солитонам, так и пакетам КВВ.

Рассмотрим более подробно разработанный алгоритм обработки данных измерений дрейфующей системой «Волна-ДС 01» (рис. 3, а). В левом столбце блок-схемы представлен ход работы с данными, получаемыми с судна (фоновыми) и с буев, в остальных – с данными только массива дрейфующих буев.

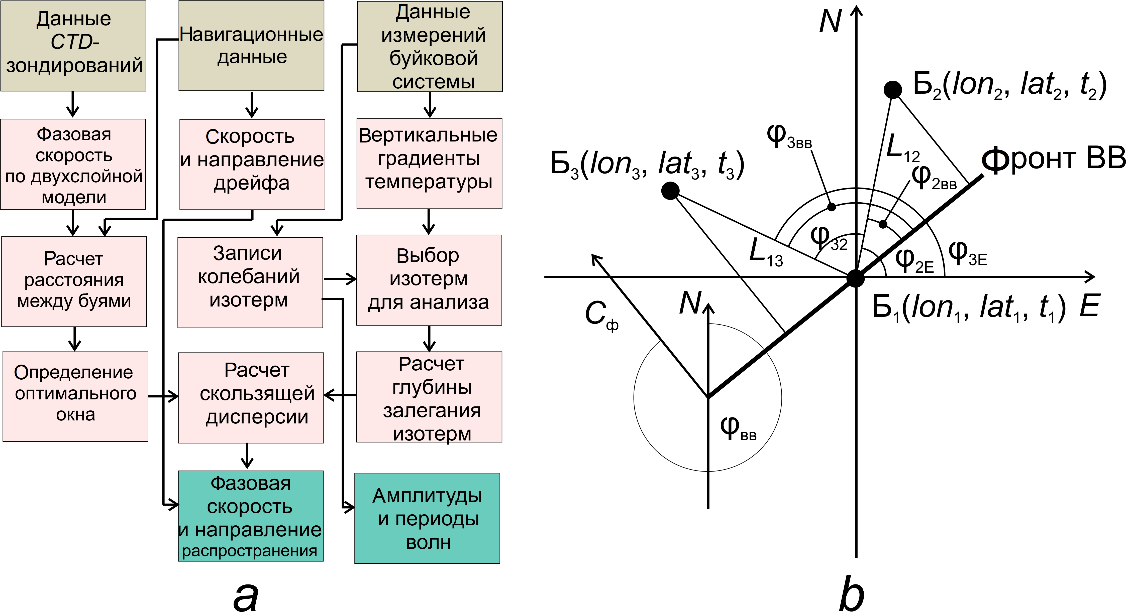
Р и с.  3. Алгоритм расчета характеристик КВВ по данным измерений дрейфующей системой: а – блок-схема алгоритма (бежевым цветом выделены исходные данные, розовым – промежуточные результаты, зеленым – конечные результаты); b – график определения скорости и направления КВВ (буквы N и E указывают направление на север и восток, крупными точками с подписями lat, lon показано географическое положение буев в момент регистрации волнового пакета, а подписями Б₁, Б₂ и Б₃ указан порядок регистрации волнового пакета буями дрейфующей системы, где Б₁ – буй, первым зарегистрировавший волновой пакет)

F i g.  3. Algorithm for calculating the SIW characteristics based on the  drifting system measurements: a – flowchart of the algorithm (beige color shows initial data, pink – intermediate results, green – final results); b – graph for determining the SIW velocities and directions (letters N and E indicate the directions to the north and east, large dots labeled lat and lon show the buoy geographical locations at the moment of wave packet recording, and signatures B₁, B₂ and B₃ indicate the order of wave packet recording by the buoys of drifting system where B₁ is the buoy that first recorded the wave packet)

На первом этапе анализа данных при расчете скользящей дисперсии возникает необходимость определения оптимального окна, в пределах которого на каждом шаге рассчитывается дисперсия. В данной работе оптимальное окно рассчитывалось как отношение среднего расстояния между буями (рассчитывается по географическим координатам буев) к фазовой скорости внутренних волн по двухслойному приближению [19] с использованием данных фоновых CTD-зондирований (см. левый столбец блок-схемы на рис. 3, а). Оптимальное окно, по сути, является минимальным временем, при котором волна распространится от одного дрейфующего буя к другому. При заниженных оценках фазовой скорости оптимальное окно может превышать период регистрируемых волн, поэтому оценка оптимального окна возможна также путем расчета минимального периода внутренних волн на записи колебаний температуры. Однако следует отметить, что истинный период волн искажается при дрейфе буев вследствие эффекта Доплера.

На рис. 3, а в среднем и правом столбцах блок-схемы показан алгоритм расчета характеристик КВВ. Отметим, что на точность и эффективность оценки разницы во времени между прибытиями пакета волн по максимумам скользящей дисперсии оказывает влияние выбор изотермы для анализа. Выбирается изотерма в слое максимального вертикального градиента температуры, глубина залегания которой испытывает максимальные по амплитуде колебания. Затем с постоянным шагом, равном дискретности измерений, рассчитываются значения глубины ее залегания, по которым определяются амплитуды и периоды КВВ в соответствии с методикой [20].

Рассчитывается скользящая дисперсия глубины залегания изотерм с учетом оценок оптимального окна и производится ее нормирование на максимальное значение для удобства последующего совместного анализа. На графиках временно́й изменчивости скользящей дисперсии производится визуальная регистрация последовательных локальных максимумов, расположенных близко по времени для разных буев дрейфующей системы. Причем, как правило, задержка между максимумами локальной дисперсии для одной пары буев из трех всегда больше, чем для другой.

Далее положение локальных максимумов валидируется путем прямого сопоставления графиков скользящей дисперсии и записей колебаний изотерм. По локальным максимумам скользящей дисперсии определяется, во-первых, порядок регистрации пакета волн буями системы, а во-вторых, моменты регистрации волнового пакета каждым из буев системы.

Затем с учетом расстояния между буями (рассчитывается по географическим координатам буев) определяется фазовая скорость КВВ [11]:

 ,                                     

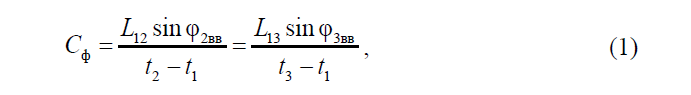где  – расстояние между буями Б₁ и Б₂;  – расстояние между буями Б₁ и Б₃; , ,  – время регистрации волнового пакета датчиками буя Б₁, Б₂ Б₃ соответственно; j_2вв – угол между прямой волнового фронта, проходящей через точку Б₁, и направлением из точки Б₁ в точку Б₂, определяемый по формуле

 ,

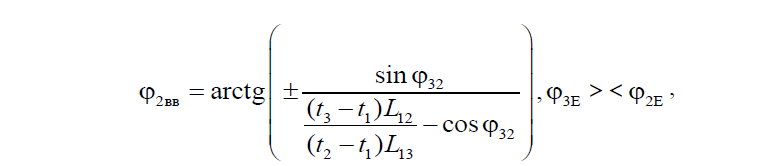где  – угол между направлениями из точки Б₁ на точку Б₂ и Б₃;  – угол между направлением из точки Б₁ на восток и на точку Б₂;  – угол между направлением из точки Б₁ на восток и на точку Б₃;  – угол между прямой волнового фронта, проходящей через точку Б₁, и направлением из точки Б₁ в точку Б₃, определяемый по формуле

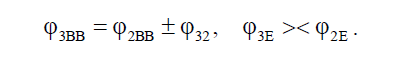
Направление распространения КВВ (рис. 3, b) определяется по формуле [11]

Существуют и другие выражения для расчета характеристик КВВ [3, 6]. Выражения из работы [11] были выбраны потому, что расчет по ним не предъявляет строгих требований к относительному положению буев и не требует перехода в другую систему координат.

По выражениям (1) и (2) рассчитываются скорость и направление распространения волны в движущейся системе отсчета, связанной с дрейфующей системой. Для получения абсолютных оценок этих величин рассчитывается векторная сумма векторов скорости волны и скорости дрейфа. При этом принимается, что буи дрейфуют с одинаковой скоростью в момент регистрации волнового пакета.

Преимущество метода, описанного в работе [11], заключается в отсутствии необходимости жесткой пространственной фиксации элементов измерительной системы. Расстояние между элементами может быть произвольным и варьироваться по пространственным масштабам в зависимости от изучаемых явлений. Алгоритм обработки результатов измерений реализован в среде Matlab. Основные операции обработки данных сопровождаются выводом графической и текстовой информации.

Результаты и их обсуждение

Характеристики КВВ в Онежском озере по данным измерений дрейфующей системой. В качестве примера применения дрейфующей системы в Онежском озере приведем результаты измерений 16 июня 2022 г. Дрейфующая система развертывалась в заливе Большое Онего над глубинами около 36 м. Для обеспечения стабильного функционирования дрейфующей системы рабочая длина термолиний была уменьшена до 30 м посредством намотки их нижней части в бухты. Расстояние между буями системы составляло ~ 300 м, а скорость дрейфа варьировалась от 0,05 до 0,1 м/с. По данным фонового CTD‑зондирования наблюдалась устойчивая температурная стратификация. Верхний квазиоднородный слой имел толщину 4 м, а слой термоклина располагался в слое от 4 до 10 м и совпадал с положением пикноклина. Градиент температуры в термоклине достигал 0,9 °С/м, что соответствовало градиенту плотности 0,08 кг/м⁴.

На рис. 4 представлены фрагменты результатов измерений в Онежском озере.

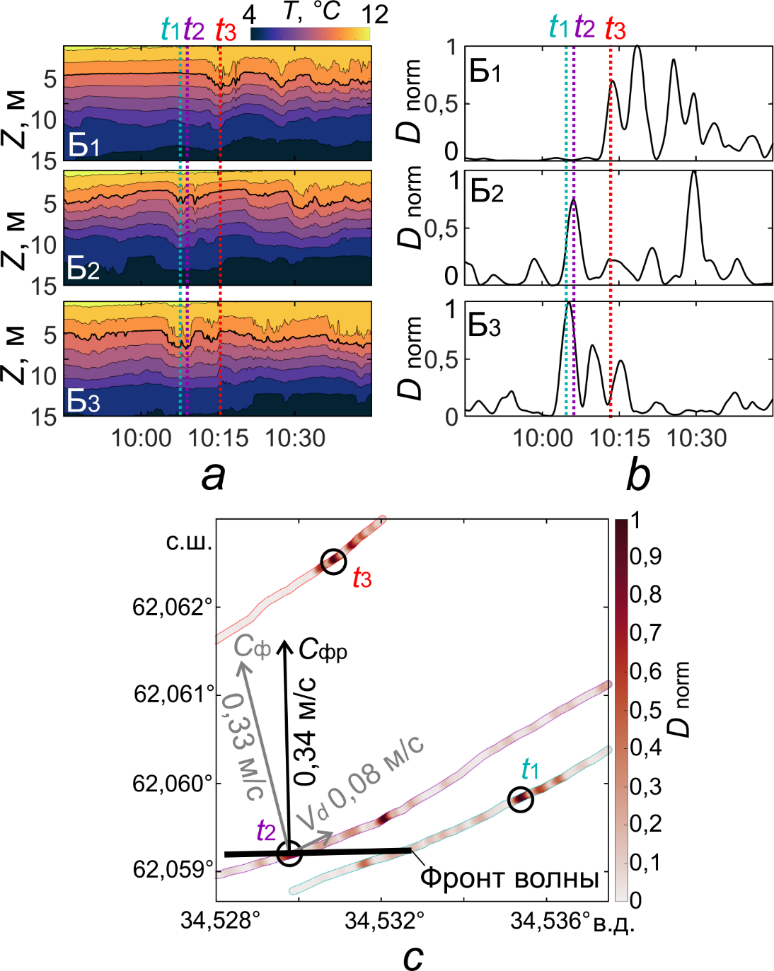
Р и с.  4. Фрагменты результатов измерений в Онежском озере в июне 2022 г. с НИС «Эколог»: а – записи колебаний изотерм для трех буев дрейфующей системы (красная пунктирная линия – буй Б₁, фиолетовая пунктирная линия – буй Б₂, бирюзовая пунктирная линия – буй Б₃; t₁, t₂, t₃ – обозначения моментов прибытия пакета волн к буям дрейфующей системы); b – временны́е вариации скользящей дисперсии, нормированные на ее максимальное значение, для глубин залегания изотермы 10 °С с окном в 5 мин; c – карта распределения скользящей дисперсии вдоль траекторий дрейфа буев с нанесенными векторами скорости дрейфа буев и скорости распространения КВВ (C_ф – фазовая скорость лидирующей волны пакета в системе отсчета, связанной с движущимися буями, V_d – скорость дрейфа буев, С_фр – результирующая фазовая скорость)

F i g.  4. Fragments of the measurement results obtained at R/V “Ecolog” in Lake Onega in June 2022: a – records of the isotherm fluctuations for three buoys of the drifting system (red dashed line is buoy B₁, purple dashed line – buoy B₂, turquoise dashed line – buoy B₃; t₁, t₂, t₃ are the designations for the moments of the wave packet arriving to the buoys of drifting system); b – time variations of the moving dispersion normalized to its maximum value for the 10 °C isotherm depths with a 5 min window; c – map of the moving dispersion distribution along the buoy drift trajectories with the vectors of buoy drift velocities and SIW phase speeds (C_ф is the phase speed of leading packet wave in the coordinate system related to the moving buoys, V_d is the buoy drift velocity and C_фр is the resulting phase speed)

На записях колебаний изотерм (рис. 4, а) по данным каждого из трех буев в слое от 4 до 10 м отмечается ярко выраженный волновой пакет с амплитудами волн ~ 1 м и периодами 10–15 мин. Исходя из записей колебаний изотерм достаточно сложно визуально выделить время прибытия пакета к буям дрейфующей системы. При расстоянии между буями 276 м и фазовой скорости по дисперсионному соотношению для двухслойной среды 0,12 м/с оптимальное окно скользящей дисперсии составляет 36 мин, что превышает максимальный период регистрируемых колебаний. Поэтому оптимальное окно скользящей дисперсии были принято равным минимальному периоду волн в 5 мин.

Расчет скользящей дисперсии для глубин залегания изотермы 10 °С (толстая черная линия на рис. 4, а), выбранной по максимуму вертикального градиента температуры, демонстрирует последовательные максимумы (рис. 4, b), которые, при сравнении с записями колебаний изотерм, хорошо соответствуют лидирующим волнам в пакете. Первый локальный максимум скользящей дисперсии (t₁) отмечался на буе 3 в 10:05 (UTC), второй (t₂) – на буе 2 в 10:06, третий (t₃) – на буе 1 в 10:18.

С учетом данных о положении буев была оценена фазовая скорость лидирующей волны пакета (0,33 м/с) по выражению (1) и направление ее распространения (350°) по выражению (2) в системе отсчета, связанной с движущимися буями. С учетом скорости дрейфа буев 0,08 м/с и направления дрейфа 38° результирующая скорость распространения пакета волн составляет 0,34 м/с, а направление – 2°.

Полученное направление распространения волнового пакета согласуется с пространственным положением локальных максимумов нормализованной скользящей дисперсии (рис. 4, c), порядком регистрации волнового пакета и оценками разницы во времени между прибытиями волнового пакета к буям системы. Скорость распространения КВВ, полученная по результатам обработки данных дрейфующей системы, в три раза превышает фазовую скорость, оцененную по двухслойной стратификации (0,34 м/с против 0,12 м/с). Вероятно, такое различие связано с тем, что зарегистрированный волновой пакет обладает значительной нелинейностью, или с тем, что двухслойное приближение не вполне корректно использовать для описания скорости внутренних волн в условиях мелководной слабостратифицированной акватории.

Отметим, что соотношение скоростей линейных и нелинейных волн часто обсуждается в контексте теории Кортвега – де Фриза (KdV), которая описывает поведение нелинейных волн, включая солитоны [21]. Эта теория показывает, что скорость нелинейных волн зависит от их амплитуды, в то время как скорость линейных волн определяется только свойствами среды (стратификацией и глубиной).

Характеристики КВВ в Карском море, по данным измерений дрейфующей системой. Рассмотрим пример обработки результатов измерений дрейфующей системой в проливе Карские Ворота 16 июля 2023 г. Буи системы устанавливались в северо-восточной части пролива (см. рис. 2) над глубинами около 80 м на расстоянии около 140 м друг от друга. По данным фонового зондирования выявлена ярко выраженная стратификация, близкая к двухслойной. Верхний квазиоднородный слой толщиной 5 м и нижний слой разделял пикноклин в слое от 5 до 11 м с градиентом плотности около 0,42 кг/м⁴. Положения пикноклина и термоклина совпадали. При данной стратификации в соответствии с дисперсионным соотношением для двухслойной среды фазовая скорость составляет 0,6 м/с.

На рис. 5 показаны фрагменты результатов измерений в проливе Карские ворота.

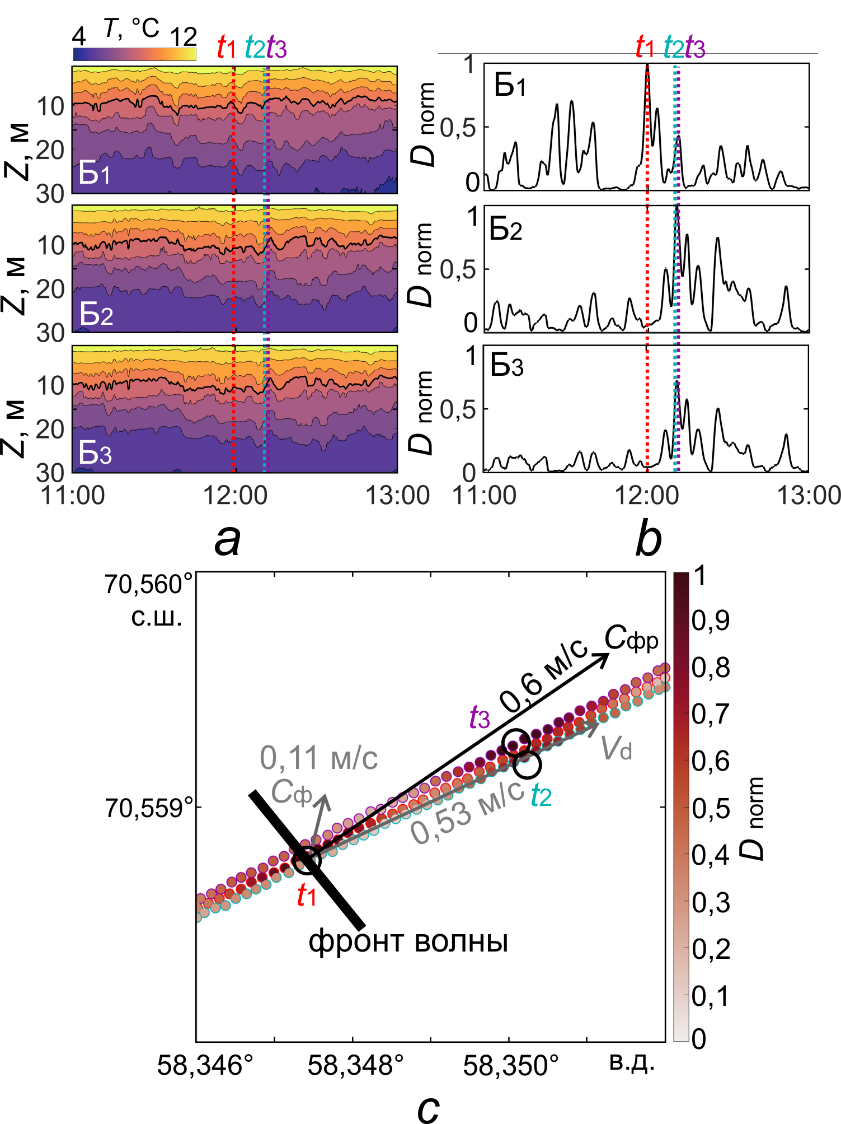
Р и с.  5. Фрагменты результатов измерений в проливе Карские Ворота в июле 2023 г. с НИС «Дальние Зеленцы» (обозначения см. в рис. 4): а – записи колебаний изотерм для трех буев дрейфующей системы; b – временны́е вариации скользящей дисперсии, нормированные на ее максимальное значение, для глубин залегания изотермы 9 °С с окном в 4 мин; c – карты распределения скользящей дисперсии вдоль траекторий дрейфа буев с нанесенными векторами скорости дрейфа буев и скорости распространения КВВ (обозначения, как в рис. 4)

F i g.  5. Fragments of the measurement results obtained at R/V “Dalnie Zelentsy” in the Kara Gate Strait in July 2023 (see designations in fig. 4): a – records of the isotherm fluctuations for three buoys of the drifting system; b – time variations of the moving dispersion  normalized to its maximum value for the 9 °C isotherm depths with a 4 min window; c – map of the moving dispersion distribution along the buoy drift trajectories with the  vectors of buoy drift velocities and SIW phase speeds (designations are as in Fig. 4)

Записи колебаний изотерм (рис. 5, а) демонстрируют наличие КВВ в слое от 5 до 15 м с амплитудами около полуметра и периодами ~ 10 мин. Сложный характер колебаний на записях не позволяет достоверно оценить время прибытия волн к буям системы. Оптимальное окно – отношение расстояния между буями (136 м) к фазовой скорости волны (0,6 м/с) – составляет 4 мин, что с учетом минимального периода регистрируемых волн, равного 5 мин, является адекватной оценкой. В области максимального градиента была выбрана изотерма 9 °С (рис 5, а). Скользящая дисперсия глубин ее залегания показана на рис. 5, b.

На всех буях дрейфующей системы отмечаются последовательные локальные максимумы, которые соответствуют сходным по форме волнам на записях колебаний изотерм. Буй 1 зарегистрировал волну в 12:01:00 (UTC) (t₁), буй 3 зарегистрировал волну в 12:11:10 (t₂), буй 2 зарегистрировал волну в 12:11:40 (t₃). Столь малая задержка связана с направлением распространения волнового пакета, малым расстоянием между буями и относительно высокой фазовой скоростью волн. Фазовая скорость, рассчитанная по выражению (1), составила 0,11 м/с, а направление распространения, вычисленное по выражению (2), составило 14°. С учетом скорости (0,53 м/с) и направления (65°) дрейфа результирующая скорость распространения волны составила 0,6 м/с, а направление – 57° (рис. 5, c). Полученная фазовая скорость близка к оценкам, полученным в двухслойной модели. Направление распространения соответствует положению и порядку регистрации максимумов дисперсии на карте дрейфа буев (рис. 5, c), а также сходно с генеральным направлением распространения проявлений пакетов КВВ, регистрируемых по спутниковым данным в районе исследований [22, 23].

Заключение

В работе описана новая гидрофизическая измерительная система на основе массива поверхностных дрейфующих термопрофилирующих буев. Основными преимуществами данной системы является ее мобильность, удобство постановки и возможность отслеживания состояния системы в режиме реального времени по спутниковому каналу связи. К недостаткам относится отсутствие штатной возможности изменения положения термодатчиков по глубине. Стоит отметить, что представленная измерительная система пригодна для регистрации широкого спектра процессов и явлений, протекающих в океане, например фронтальной и вихревой динамики.

Были описаны методические особенности оценки скорости и направления внутренних волн. Продемонстрирован способ определения времени задержки прибытия волновых пакетов к измерителям по результатам расчета скользящей дисперсии с окном, определяемым исходя из условий стратификации, конфигурации дрейфующей системы и периода регистрируемых волн.

Представлены результаты применения системы в Онежском озере и в проливе Карские ворота. Обработка результатов измерений с использованием предложенного метода на основе расчета скользящей дисперсии позволила определить фазовую скорость и направление распространения КВВ.

Сравнивая результаты, полученные в Онежском озере и проливе Карские Ворота, стоит отметить, что при уменьшении расстояния между буями усложняется оценка задержки прибытия волновых пакетов, поскольку разница между максимумами скользящей дисперсии оказывается малой. Это важно учитывать в последующих работах, развертывая буи так, чтобы расстояние между ними было примерно равным длине исследуемой волны.

В результате применения дрейфующей системы «Волна-ДС 01» в 2022–2024 гг. накоплена обширная база натурных измерений. Полученные характеристики волн в дальнейшем, в совокупности с результатами спутниковых наблюдений и расчетов по региональной приливной модели высокого разрешения, позволят определить преобладающие механизмы генерации КВВ в различных районах Карского моря.

В дальнейшем представленный алгоритм будет усовершенствован. Планируется более детальный сравнительный анализ различных методов оценки времени задержки сигналов, а также применение иных способов оценки скорости и направления волн. Для валидации оценок фазовой скорости будут использоваться данные о полном профиле плотности, а период регистрируемых волн будет корректироваться с учетом эффекта Доплера.

1. Spirals on the Sea / W. Mink [et el.] // Proceedings of The Royal Society A: Mathematical, Physical And Engineering Sciences. 2000. Vol. 456, iss. 1997. Р. 1217–1280. https://doi.org/10.1098/rspa.2000.0560

2. Зимин А. В. Субприливные процессы и явления в Белом море. Москва : ГЕОС, 2018. 220 с. EDN FNLVTS.

3. Примеры подходов к исследованию температурной изменчивости вод шельфа Черного моря при помощи кластера термокос / В. В. Очередник [и др.] // Океанология. 2020. Т. 60, № 2. С. 173–185. EDN YCLUGL. https://doi.org/10.31857/S0030157420010189

4. Internal Waves Study on a Narrow Steep Shelf of the Black Sea Using the Spatial Antenna of Line Temperature Sensors / A. Serebryany [et al.] // Journal of Marine Science and Engineer-ing. 2020. Vol. 8, iss. 11. 833. https://doi.org/10.3390/jmse8110833

5. Multi-Sensor Observations Reveal Large-Amplitude Nonlinear Internal Waves in the Kara Gates, Arctic Ocean / I. E. Kozlov [et al.] // Remote Sens. 2023. Vol. 15, iss. 24. 5769. https://doi.org/10.3390/rs15245769

6. Степанюк И. А. Методы измерений характеристик морских внутренних волн. Санкт-Петербург : РГГМУ, 2002. 138 с. EDN RXGVIT.

7. Мотыжев С. В., Лунев Е. Г., Толстошеев А. П. Опыт применения автономных дрифтеров в системе наблюдений ледовых полей и верхнего слоя океана в Арктике // Морской гидрофизический журнал. 2017. № 2. С. 54–68. EDN XTCKW. https://doi.org/10.22449/0233-7584-2017-2-54-68

8. Толстошеев А. П., Лунев Е. Г., Мотыжев В. С. Развитие средств и методов дрифтерной технологии применительно к проблеме изучения Черного моря // Океанология. 2008. Т. 48, № 1. С. 149–158. EDN IBYVLJ.

9. Система мониторинга характеристик гидрофизических полей в субмезомасштабном ин-тервале изменчивости / А. В. Зимин [и др.] // Моря России: год науки и технологий в РФ – десятилетие наук об океане ООН : тезисы докладов Всероссийской научной кон-ференции. Севастополь, 2021. С. 246–247. EDN SXOYCH.

10. Метод оценки характеристик короткопериодных внутренних волн по данным массива дрейфующих буев / Е. И. Свергун [и др.] // Моря России: от теории к практике океаноло-гических исследований : тезисы докладов Всероссийской научной конференции. Севасто-поль, 2023. С. 102–103. EDN KIAQSP.

11. Centurioni L. Observations of Large-Amplitude Nonlinear Internal Waves from a Drifting Ar-ray: Instruments and Methods // Journal of Atmospheric and Oceanic Technology. 2010. Vol. 27, iss. 10. P. 1711–1731. https://doi.org/10.1175/2010JTECHO774.1

12. Lee O. S. Observations on internal waves in shallow water // Limnology and Oceanography. 1961. Vol. 6, iss. 3. P. 312–321. https://doi.org/10.4319/lo.1961.6.3.0312

13. Observations of internal waves generated by an anticyclonic eddy: a case study in the ice edge region of the Greenland Sea / O. M. Johannessen, [et al.] // Tellus, Series A: Dynamic Meteor-ology and Oceanography. 2019. Vol. 71, iss.1. P. 1–12. https://doi.org/10.1080/16000870.2019.1652881

14. On the identification of internal solitary waves from moored observations in the northern South China Sea / Q. Gong [et al.] // Scientific Reports. 2023. Vol. 13, iss. 1. 3133. https://doi.org/10.1038/s41598-023-28565-5

15. Севостьянов П. А., Самойлова Т. А., Родин А. А. Последовательные регрессии при анали-зе и прогнозировании вариабельности временных рядов // Инновационные технологии в текстильной и легкой промышленности : материалы Международной научно-технической конференции. 2019. С. 305–307. EDN QMAKUP.

16. Свердлик Л. Г. Идентификация предсейсмических возмущений в атмосфере с использо-ванием модифицированного критерия STA/LTA // Современные проблемы дистанцион-ного зондирования Земли из космоса. 2021. Т. 18, № 3. С. 141–149. EDN FXVUDP. https://doi.org/10.21046/2070-7401-2021-18-3-141-149

17. Саидов О. А. Мониторинг вариаций газогеохимических параметров в области Дагестан-ский клин в связи с сейсмическими событиями // Мониторинг. Наука и технологии. 2014. № 4. С. 71–75. EDN TDXDBP.

18. Using Moving Variance Method to Detect Ocean Currents from Space / A. V. Khodyaev [et al.] // Journal of Siberian Federal University. Engineering and Technologies. 2011. Vol. 4, iss. 2. P. 179–184. EDN NMWLLF.

19. Коняев К. В., Сабинин К. Д. Волны внутри океана. Cанкт-Петербург : Гидрометеоиздат, 1992. 269 с.

20. Жегулин Г. В., Зимин А. В., Родионов А. А. Анализ дисперсионных зависимостей и верти-кальной структуры внутренних волн в Белом море по экспериментальным данным // Фундаментальная и прикладная гидрофизика. 2016. Т. 9, № 4. С. 47–59. EDN XELWCH.

21. Remote sensing techniques for detecting internal solitary waves: A comprehensive review and prospects / J. Meng [et al.] // IEEE Geoscience and Remote Sensing Magazine. 2024. Vol. 12, iss. 4. P. 46–78. https://doi.org/10.1109/MGRS.2024.3402673.

22. Районы генерации нелинейных внутренних волн в Баренцевом, Карском и Белом морях по данным спутниковых РСА измерений / И. Е. Козлов [и др.] // Современные проблемы дистанционного зондирования Земли из космоса. 2014. Т. 11, № 4. С. 338–345. EDN TJELGP.

23. Properties of Short-Period Internal Waves in the Kara Gates Strait Revealed from Spaceborne SAR Data / I. O. Kopyshov [et al.] // Russian Journal of Earth Sciences. 2023. Vol. 23, iss. 5. ESO210. EDN QJSLVL. https://doi.org/10.2205/2023ES02SI10