Введение
Нам известны лишь две публикации, темой которых является оценка изменений климатических характеристик под действием диапикнического перемешивания, индуцированного диссипацией бароклинного прилива [1, 2]. Они основываются не на данных in situ измерений в море, а на сравнении модельных профилей средних (за приливный цикл и по площади моря) коэффициентов вертикальной турбулентной и диапикнической диффузии, индуцируемых неприливным (ветровым + термохалинным + обусловленным массообменом с соседними водоемами) и чисто приливным форсингами. Естественно, что полученные в указанных работах выводы относительно важности изменений климатических характеристик в море, вызванных диссипацией бароклинного прилива, могут рассматриваться как ориентировочные до появления новой эмпирической информации. Поскольку, однако, появление сколько-нибудь многочисленных данных прямых измерений в море в бли-жайшем будущем вряд ли возможно, мы видели цель настоящего сообщения в том, чтобы, используя предложенный в [2] косвенный способ описания дис-сипации бароклинной приливной энергии, оценить роль приливов в форми-ровании климатических характеристик в море с использованием результатов высокоразрешающего моделирования.
Косвенный способ описания эффектов внутренних приливных волн (ВПВ) и используемая модель
Остановимся вкратце на том, что лежит в основе косвенного способа описания диапикнической диффузии. Объяснение механизма ее возникнове-ния следующее: предполагается, что диапикническая диффузия обязана сво-им происхождением не орографическому сопротивлению, как это считалось в [3], а диссипации бароклинной приливной энергии, входящей в выражение для коэффициента диапикнической диффузии [4]. Сложение нескорректиро-ванного коэффициента вертикальной турбулентной диффузии, контролируе-мого неприливными форсингами, с коэффициентом диапикнической диффу-зии дает возможность оценить скорректированный (с учетом эффектов ВПВ) коэффициент вертикальной турбулентной диффузии. Обоснованием служит приближение «слабого взаимодействия» [5], согласно которому если раз-ность характерных частот и пространственных масштабов турбулентности различного происхождения достаточно велика, то нелинейными взаимодей-ствиями между ее отдельными составляющими можно пренебречь, прибли-женно полагая их аддитивными, хотя сами по себе эти составляющие турбу-лентности являются сильно нелинейными. Решение исходной начально-краевой задачи, характеризующей климат моря, ищется в такой последова-тельности: сначала решаются две вспомогательные задачи – одна, отвечаю-щая неприливным форсингам, и другая, описывающая динамику и энергети-ку ВПВ в море под действием чисто приливного форсинга. Из решения пер-вой задачи находится соответствующий ей нескорректированный коэффици-ент вертикальной турбулентной диффузии, из решения второй – средний (за приливный цикл) коэффициент диапикнической диффузии. Затем нескоррек-тированный коэффициент вертикальной турбулентной диффузии корректи-руется суммированием со средним локальным коэффициентом диапикниче-ской диффузии, после чего уравнения гидротермодинамики моря при скор-ректированном коэффициенте вертикальной турбулентной диффузии инте-грируются до выхода решения на квазистационарный режим. Сравнение двух решений, полученных с учетом и без учета эффектов ВПВ, дает представле-ние о приливных изменениях климатических характеристик в море. Здесь и далее под приливными изменениями климатических характеристик пони-маются изменения, обусловленные диапикнической диффузией, определяе-мой эффектами ВПВ. Преимуществом такого способа описания является от-каз от двух априорных предположений, принятых в [3], а именно: о неизмен-ности в горизонтальной плоскости вертикального распределения диссипации бароклинной приливной энергии и о фиксации вертикального масштаба вы-рождения диссипации (задание его равным значению, найденному в Бразиль-
ской котловине), как это делается при определении диссипации через оро-графическое сопротивление. Оба предположения дискуссионны, имея в виду пятнистость структуры диссипации в океане.
Отметим, что все выполненные до сих пор исследования обсуждаемого вопроса касались главным образом океанских масштабов. Региональных ис-следований подобного рода не проводилось, кроме, пожалуй, описанных применительно к Баренцеву и Карскому морям в [1, 2]. Имея это в виду, настоящая работа может или подтвердить сделанные в [1, 2] выводы, или опровергнуть их. Для достижения поставленной цели использовалась трех-мерная конечно-элементная гидростатическая модель QUODDY-4 [6]. Огра-ничимся перечислением модельных уравнений, используемых в ней, и опи-санием принятой в модели специальной процедуры определения бароклинно-го градиента давления и граничных условий на свободной поверхности моря и его дне (точнее, на ближайшем ко дну расчетном уровне). Здесь также пе-речисляются используемые источники эмпирической информации.
Модель включает так называемое двумерное обобщенное уравнение не-разрывности в волновой форме для возмущений уровня свободной поверхно-сти моря, непреобразованные уравнения движения, записанные в приближе-ниях гидростатики и Буссинеска, эволюционные уравнения для температуры и солености морской воды и характеристик турбулентности (кинетической энергии турбулентности (КЭТ) и масштаба турбулентности), трехмерное уравнение неразрывности, служащее для определения вертикальной скорости и уравнения гидростатики и состояния морской воды. Эволюционные урав-нения для горизонтальной скорости, температуры и солености морской воды и характеристик турбулентности после перенесения членов, характеризую-щих адвекцию и горизонтальную турбулентную диффузию на предыдущий шаг по времени, решаются как система нестационарных одномерных (по вер-тикали) неоднородных дифференциальных уравнений.
В принятой модели используется специальная процедура определения бароклинного градиента давления. Ее суть сводится к следующему: плот-ность морской воды на фиксированном горизонте интерполируются с σ-коор-динатной сетки на z-координатную, после чего бароклинный градиент давле-ния рассчитывается на z-координатной сетке и затем интерполируется назад на σ-координатную сетку, на которой и проводится вертикальное интегриро-вание уравнений модели.
Граничные условия для КЭТ на свободной поверхности и ближайшем ко дну расчетном уровне задаются условием Дирихле, вытекающим из прибли-женного равенства между продукцией и диссипацией КЭТ при аппроксима-ции масштаба турбулентности законом стенки и связывающим кинетическую энергию турбулентности с квадратом скорости трения. Граничные значения масштаба турбулентности там же находятся из закона стенки. Необходимый для определения горизонтальной скорости вертикальный поток импульса на границе раздела вода – воздух выражается через поток импульса в приводном слое атмосферы, который параметризуется квадратичным законом сопротив-ления с коэффициентом сопротивления, равным 1,3 × 10–3. Так же параметри-зуется поток импульса в придонном слое моря. Коэффициент сопротивления в этом случае принимается равным 5,0 × 10–3. Коэффициенты горизонтальной турбулентной диффузии рассчитываются по известной формуле Смагоринского.
Ветровой и термохалинный форсинги, а также уровень моря на открытой границе расчетной области задаются климатическими, соответствующими летнему (июль, август) безледному периоду в море Лаптевых. Поле ветра в приводном слое атмосферы берется из ERA-Interim реанализа атмосферных данных в Арктике, признанного сейчас наилучшим из 7 имеющихся продуктов реанализа [7]. Значения уровня на свободной поверхности моря задаются по данным CNES-CLS09 глобальной средней динамической топографии свободной поверхности моря, дополненной данными спутниковой альтиметрии и in situ измерений [8]. Температура и соленость морской воды на свободной поверхности моря определяются с помощью восстанавливающих (restoring)
граничных условий, в соответствии с которыми нормированные потоки тепла и соли на свободной поверхности моря считаются пропорциональными разностям климатических и предсказываемых значений переменных с коэффициентом пропорциональности, имеющим смысл обратного времени восстановления. Последнее принимается одинаковым для температуры и солености морской воды и равным 105 с, т. е., согласно [9], восстановление предсказываемых значений температуры и солености к их климатическим значениям считается сильным. Климатические значения переменных берутся из цифрового атласа Арктики [10], потоки тепла и соли на ближайшем ко дну расчетном уровне принимаются равными нулю. Море считается стратифицированным и свободным от морского льда и речного стока, что избавляет от необходимости рассматривать их последствия.
Горизонтальное разрешение конечно-элементной сетки принимается в среднем по площади моря равным 5 км. Вводится отслеживающая топографию дна вертикальная координата с неравномерным распределением слоев по вертикали. Толща моря делится на 40 слоев (переменной протяженности по глубине), сгущающихся в поверхностном и придонном пограничных слоях. Шаг по времени задается равным 24 с. Необходимость выбора такого временного шага диктуется решением эволюционных уравнений для горизонтальной скорости, температуры и солености морской воды и характеристик турбулентности как системы нестационарных одномерных (по вертикали) неоднородных дифференциальных уравнений. Глубины заимствуются из банка данных IBCAO. Остальные параметры модели задаются такими же, как и в ее оригинальной версии [6]. Коэффициент диапикнической диффузии, необходимый для реализации косвенного способа учета приливного форсинга, задается по результатам работы [11].
Результаты моделирования
Приступая к обсуждению результатов моделирования, отметим, что индуцируемые ВПВ приливные изменения климатических характеристик в море охватывают, как правило, все море (рис. 1–7) в противоположность ожиданиям, согласно которым они не проникают за пределы критической широты (на ней приливная и инерционная частоты совпадают; в нашем случае для волны М2 она равна 74,5° с. ш.). Иначе говоря, область существования ВПВ  как свободно перемещающихся волн ограничивается критической широтой. Здесь ВПВ дезинтегрируются (распадаются) в пакеты нелинейных короткопериодных внутренних волн (КВВ). Вообще говоря, отражение ВПВ от критической широты также не исключено. В полной мере они не воспроизводятся ни одной приливной моделью (и используемой здесь в том числе), так что КВВ могут распространяться только от источника их генерации, и существование приливных изменений не может быть связано с ними. Возникает вопрос, чем тогда вызваны КВВ в сверхкритических широтах? Можно предполагать, оставаясь в рамках классической теории динамики приливов, что на критической широте происходит либо частичная дезинтеграция ВПВ и, следовательно, допустить существование вырожденных ВПВ в сверхкритических широтах, либо полная дезинтеграция ВПВ и, значит, признать существование еще каких-то неустановленных до сих пор источников генерации ВПВ в сверхкритических широтах, о чем свидетельствуют данные анализа SAR-изображений морской поверхности (см., напр., [12]). Не кажется невозможным и существование в сверхкритических широтах квазиинерционных внутренних волн *.

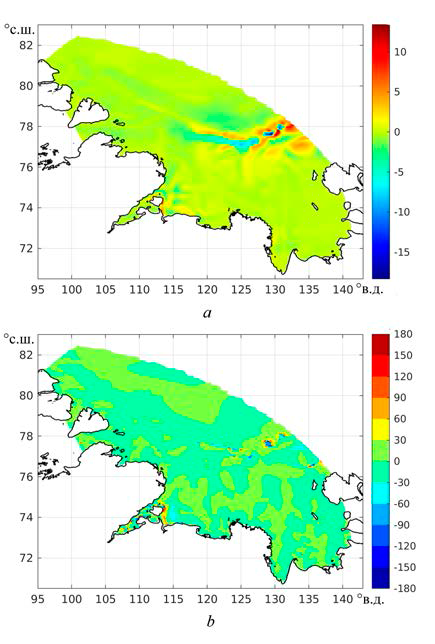
Р и с. 1. Приливные изменения модуля (м/с) – a и направления (°) – b результирующей скоро-
сти постоянных течений в поверхностном слое моря
F i g. 1. Tidal changes of magnitude (m/s) – a and direction (°) – b of the stationary current resulting velocity in the sea surface layer
* Черкесов Л. В. Гидродинамика поверхностных и внутренних волн. Киев : Наукова дум-
ка, 1976. 364 c.

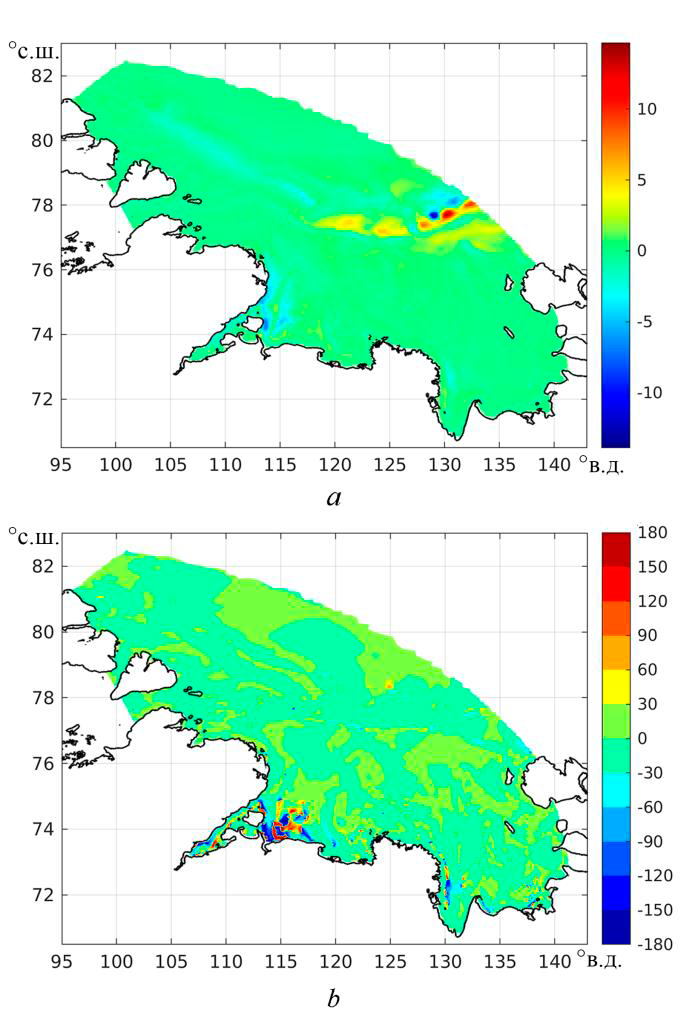
Р и с. 2. То же, что на рис. 1, для результирующей скорости постоянных течений в придонном слое моря
F i g. 2. The same as in Fig. 1 for the stationary current resulting velocity in the sea bottom layer

Во втором случае, однако, придется объяснить, какие именно волны представляют собой источник множественной генерации ВПВ в сверхкрити-ческих широтах. Чтобы это понять, требуется решить прежде всего еще одну вспомогательную задачу – доказать, что полученные результаты не являются модельно-зависимыми. Пока названная задача не решена, приведенные ре-зультаты можно воспринимать как ориентировочные, предназначенные для оценок порядков величин интересующих нас характеристик. Косвенным под-тверждением сказанного могут служить результаты высокоразрешающего моделирования ВПВ в море Лаптевых, приведенные в [13], прямым – резуль-таты полевых измерений, изложенные в [14–17]. Будем полагать в дальней-шем, что возможным объяснением  тах. Это – первое обстоятельство, на которое хотелось бы обратить внимание. Второе – то, что средние (за приливный цикл и по площади моря) приливные изменения модуля и направления результирующих скоростей постоянных течений в поверхностном слое моря (рис. 1) составляют –0,1 см/с и –0,4° со-ответственно и только на свале глубин в северной части континентального склона (77,75° с. ш., 130,52° в. д.) они достигают бóльших значений (макси-мум 13,4 см/с и 8,6°). То же самое можно сказать в отношении результирую-щих скоростей в придонном слое моря (рис. 2) с той лишь разницей, что те-перь приливные изменения модуля скорости в той же точке равны 13,1 см/с, направления –3,8°. Как видно, отличия приливных изменений результирую-щих скоростей в указанных слоях не очень велики, что неявно наводит на мысль о баротропизации скоростей, входящих в определение их приливных изменений.

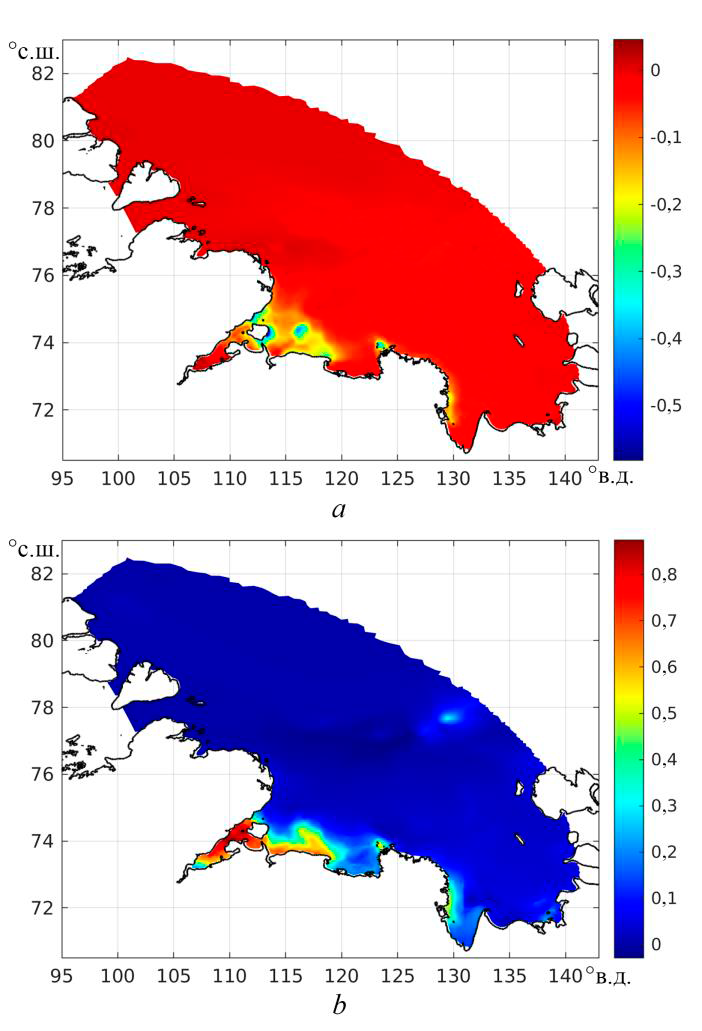
Р и с. 3. Приливные изменения температуры морской воды (°С) в поверхностном (а) и при-донном (b) слоях моря
F i g. 3. Tidal changes of sea water temperature (°С) in the surface (a) and bottom (b) layers

На рис. 3 приводятся поля приливных изменений температуры морской воды в поверхностном и придонном слоях моря. Из него следует, что отличи-тельной особенностью этих полей является почти однородная (в горизон-тальной плоскости) структура, охватывающая практически все море, кроме заливов в юго-восточной части. Приливные изменения температуры в по-верхностном слое составляют –0,1–0,0°С, в придонном 0,0–0,1°С. Наиболее заметные отличия от такой структуры обнаруживаются у открытой границы Хатангского залива в районе о. Большой Бегичев, где приливные изменения достигают –0,4°С, тогда как в основной части Анабарского залива они равны –0,2°С. К востоку приливные изменения температуры затухают всюду в Оле-некском заливе, кроме окрестностей его восточного побережья, и затем в ви-де узкой полосы, окаймляющей побережье материка, наблюдаются у запад-ного побережья губы Буор-Хая.
В придонном слое наиболее заметные приливные изменения температу-ры морской воды прослеживаются в основной части Хатангского залива до северного берега о. Большой Бегичев и далее в виде узкой полосы, примыка-ющей к побережью материка, охватывают б. Нордвик, а также Анабарский и Оленекский заливы. При этом приливные изменения температуры посте-пенно уменьшаются в восточном направлении. На границе Хатангского зали-ва они составляют 0,7–0,8°С, такой же порядок величины они имеют в б. Нордвик, затем уменьшаются до 0,5–0,6°С в Анабарском заливе и далее к востоку в Оленекском заливе достигают 0,4°С, а в западной части губы Буор-Хая вновь несколько растут до 0,5°С. Подчеркнем повсеместный рост приливных изменений температуры в придонном слое, особенно в Хатанг-ском и других перечисленных выше заливах, по сравнению с поверхностным слоем.
Наличие обширной структуры с почти однородными (в горизонтальной плоскости) приливными изменениями солености морской воды характерно и для полей, приведенных на рис. 4. Единственное отличие – увеличение приливных изменений солености до 1,3‰ в окрестности северного берега о. Большой Бегичев в поверхностном слое, еще более сильное уменьшение до 0,5‰ в основной части Хатангского залива и б. Нордвик; наоборот, более слабое уменьшение приливных изменений солености до 0,3‰ в Анабарском заливе и, наконец, почти полное исчезновение подобных изменений в Оле-некском заливе и губе Буор-Хая. Это относилось главным образом к поверх-ностному слою. В придонном слое приливные изменения солености преобра-зуются из положительных в поверхностном слое в отрицательные. При этом в Хатангском заливе, б. Нордвик и Анабарском заливе их величины состав-ляют –2,5 … –2,0‰, затем далее к Оленекскому заливу они увеличиваются до –0,7‰, после чего вновь уменьшаются до –2,0‰ на восточной границе Оле-некского залива и до –1,5‰ и меньше – в окрестности западного побережья губы Буор-Хая.

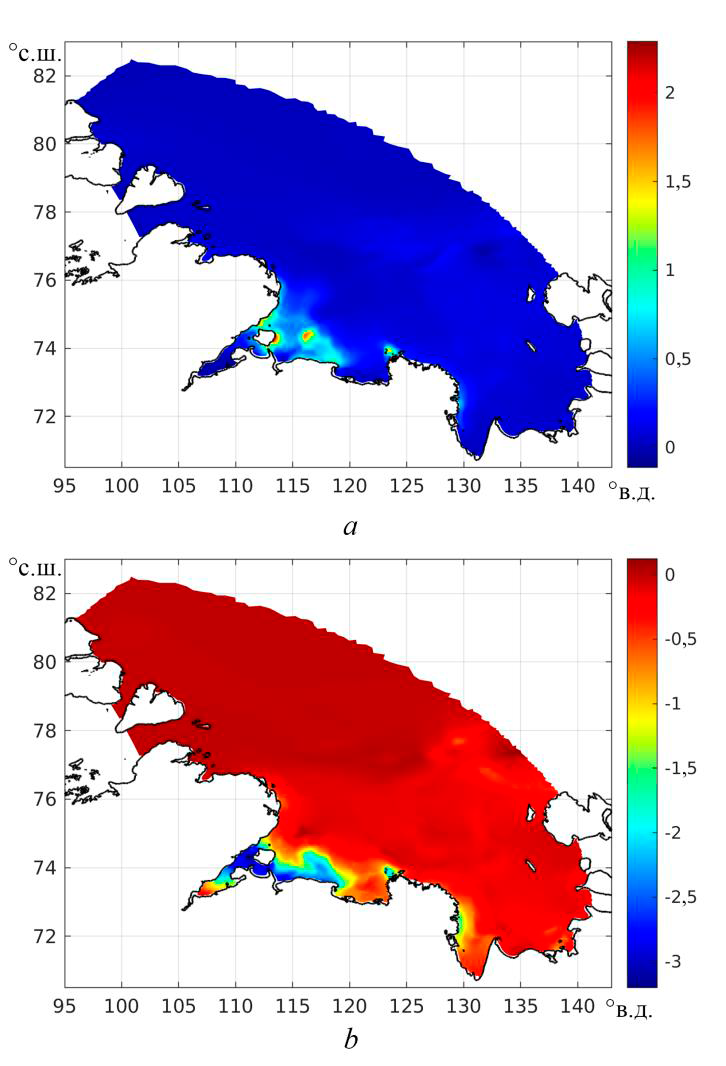
Р и с. 4. То же, что на рис. 3, для солености морской воды (‰)
F i g. 4. The same as in Fig. 3 for sea water salinity (‰)

На рис. 5 и 6 показаны приливные изменения температуры и солености морской воды вдоль меридиана 120° в. д. В основной толще моря их величи-ны достигают 0,03°С для температуры и изменяются в пределах –0,05 … 0,05‰ для солености, выклиниваясь с увеличением расстояния к северу. За-метим, что выклинивание приливных изменений температуры и солености морской воды может иметь своей причиной вырождение ВПВ. Указанные рисунки интересны еще в одном отношении – как свидетельство того, что основные приливные изменения этих переменных приходятся не на поверх-ностный слой, а на нижние слои моря, в том числе и на придонный. Здесь приливные изменения температуры в мелководной части разреза больше, чем в поверхностном слое, в разы, а приливные изменения солености там же ва-рьируются в пределах 0,5 … –1,0‰.

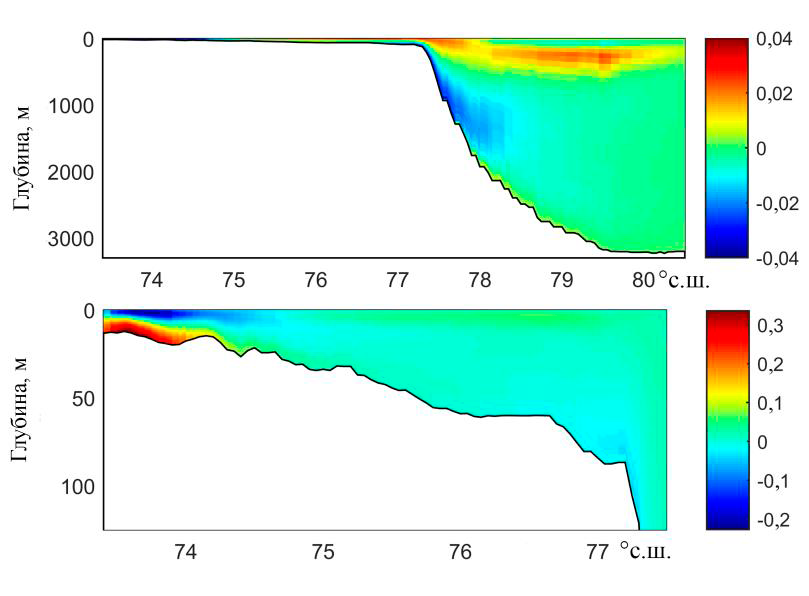
Р и с. 5. Приливные изменения температуры морской воды (°С) вдоль меридионального раз-реза 120° в. д. На верхнем фрагменте они показаны вдоль всего разреза, на нижнем – вдоль его мелководной части в увеличенном масштабе
F i g. 5. Tidal changes of sea water temperature (°С) along the meridional transect 120° E. In the upper fragment, the tidal temperature changes are shown along the entire section, in the lower frag-ment – along its shallow-water part on the enlarged scale

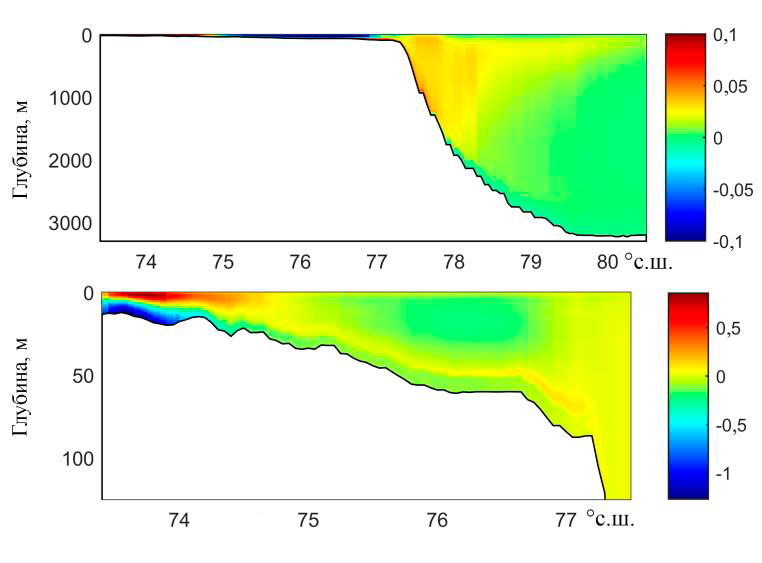
Р и с. 6. То же, что на рис. 5, для солености морской воды (‰)
F i g. 6. The same as in Fig. 5 for sea water salinity (‰)

Еще одна особенность приливных изменений климатических характери-стик в море связана с полем приливных изменений уровня моря (рис. 7). Оно обладает четко выраженной полосчатой структурой, отдаленно напоминаю-щей очертания континентального склона. Величина приливных изменений уровня в этой структуре составляет ± 0,06 м, от понижения уровня (–0,06 м) в окрестности континентального склона до повышения (0,04 м и выше) на мелководье к востоку от континентального склона, и остается близкой к ну-левым значениям в западной и восточной частях моря.

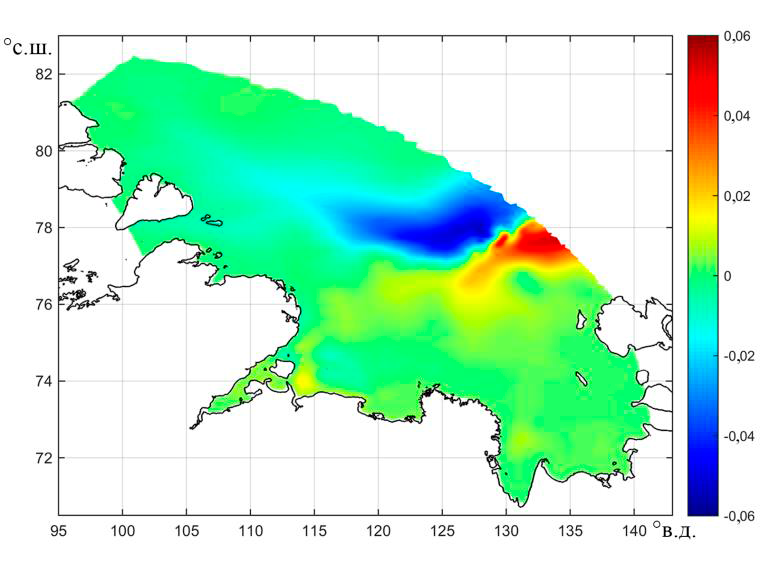
Р и с. 7. Приливные изменения уровня моря (м)
F i g. 7. Tidal changes of the sea surface level (m)

Известно, что для моря Лаптевых характерно деление глубин на две об-ласти – мелководную (внутренний шельф) и глубоководную (внешний шельф). В первой из них вертикальная турбулентная диффузия может рас-пространяться на всю толщу моря, во второй, включающей стратифициро-ванную часть водной толщи, может происходить генерация ВПВ, но только до критической широты. Как уже говорилось, ВПВ дезинтегрируются в паке-ты нелинейных КВВ, так что в сверхкритических широтах ВПВ не могут свободно распространяться. Какие именно из неустановленных волн способ-ны на это, пока не известно. Известно только, что вблизи критической широ-ты КВВ существенно отличаются от ВПВ и что, по-видимому, одним из ве-роятных механизмов их генерации является тот, который присущ подветрен-ным волнам, индуцируемым на подветренной стороне подводных препят-ствий [17]. Следовательно, в настоящее время мы располагаем двумя объяс-нениями механизма генерации КВВ в сверхкритических широтах. Одно из них, упомянутое выше, связывает КВВ с частичной дезинтеграцией ВПВ на критической широте в пакеты КВВ и с последующим распространением КВВ, равно как и вырожденных ВПВ, служащих источником генерации дру-гих КВВ в сверхкритических широтах. Второе объяснение истолковывает КВВ как подветренные внутренние волны, образующиеся на подветренной стороне неровностей морского дна типа кромки шельфа и изолированного поднятия дна [18]. Такое объяснение конкретизирует механизм генерации КВВ, но не раскрывает их происхождения в сверхкритических широтах. Ка-кое из представленных здесь объяснений предпочтительнее, еще предстоит выяснить.
Можно ожидать, что приливные изменения климатических характери-стик в море встречаются и в мелководной, и в глубоководной областях. Ожи-дания, однако, оправдываются только частично: средние (за приливный цикл и по площади моря) скорректированный (за счет эффектов ВПВ) и нескор-ректированный коэффициенты вертикальной турбулентной диффузии отли-чаются друг от друга меньше чем на порядок величины, и только в зоне IV (рис. 8) их расхождения оказываются больше в слое, расположенном глубже горизонта 2500 м. Чтобы приведенное здесь заключение о вертикальном рас-пределении двух коэффициентов стало понятнее, выделим в море мелковод-ную область с глубинами до 100 м (зона I), окаймляющую континентальный склон область с глубинами 100–500 м (зона II), примыкающую к ней с севера область с глубинами 500–2500 м (зона III) и глубоководную область с глуби-нами, большими 2500 м (зона IV). В каждой такой области определяются средние скорректированный и нескорректированный коэффициенты верти-кальной турбулентной диффузии. Из рис. 9 следует, что индуцированные ВПВ расхождения величин указанных коэффициентов сосредоточены пре-имущественно в нижних слоях, объем которых относительно объема моря в целом составляет  40%. Отмеченное обстоятельство дает основание пола-гать, что наибольшие приливные изменения климатических характеристик, в частности температуры и солености морской воды, находятся в нижних, а не в верхних слоях моря.

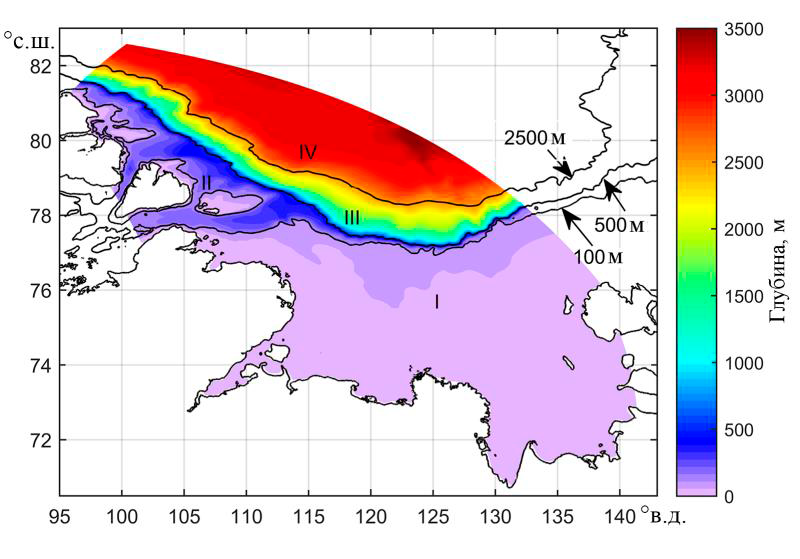
Р и с. 8. Топография дна и зоны моря с разными глубинами
F i g. 8. Bottom topography and the specific zones with different depths

Теперь, когда получены оценки приливных изменений температуры и солености в море, встает задача сравнения результатов моделирования с данными наблюдений. Однако ее выполнение затруднено в связи с отсут-ствием массовых измерений некоторых из климатических характеристик в море. Из 5 таких характеристик (модуль и направление результирующей скорости постоянных течений, температура и соленость морской воды, уро-

вень свободной поверхности моря) только температура и соленость обладают необходимыми данными. От сравнения остальных в связи с малочисленно-стью данных наблюдений приходится отказаться. По результатам моделиро-вания, средние (за приливный цикл и по площади моря) приливные измене-ния температуры и солености морской воды, определяемые как разности их предсказываемых с учетом эффектов ВПВ значений и отсчетных значений, контролируемых только неприливными форсингами и тем самым не учиты-вающих эффекты ВПВ, равны –0,02°С и 0,10‰ в поверхностном слое и 0,05°С и –0,20‰ – в придонном. Их сравнение с соответствующими клима-тическими характеристиками показывает, что они соизмеримы с одноимен-ными климатическими характеристиками для температуры и много меньше – для солености. Отсюда следует, что общепринятое игнорирование приливных изменений температуры и солености в море оправдано для солености и ли-шено оснований для температуры морской воды. Так ли это в общем случае, предстоит выяснить. О возможных причинах появления подобных оценок приливных изменений температуры и солености морской воды см. ниже.

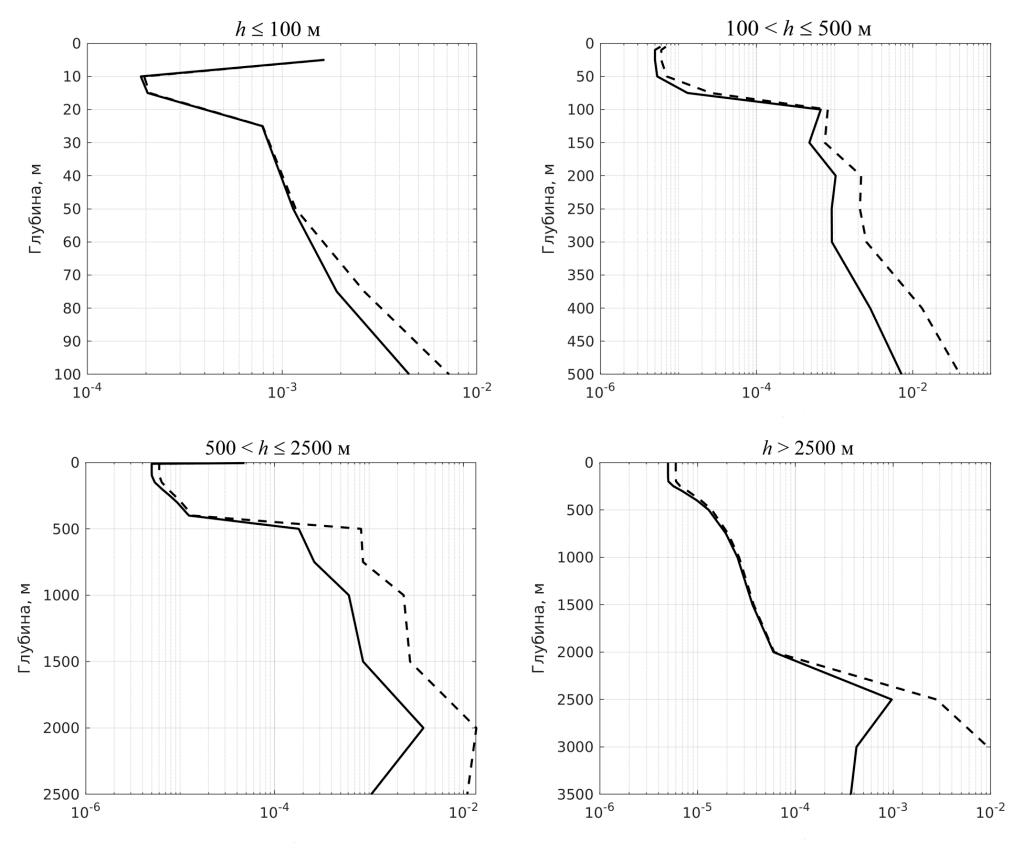
Р и с. 9. Вертикальные профили средних (по площади той или иной зоны) значений нескор-ректированного (сплошная линия) и скорректированного (штриховая) (за счет эффектов ВПВ) коэффициентов вертикальной турбулентной диффузии (м2/с)
F i g. 9. Vertical profiles of the average (over the area of any specific zone) values of the non-corrected (solid line) and corrected (dashed line) (due to the ITW effects) coefficients of vertical tur-bulent diffusion (m2/s)

Рассмотрим, как разнятся между собой наблюдаемые и модельные при-ливные изменения температуры и солености морской воды. Здесь мы сталки-ваемся с необходимостью оценивания отсчетных значений температуры и солености по данным наблюдений. Дело в том, что данные наблюдений несут на себе отпечатки всех рассматриваемых форсингов, включая прилив-ный, тогда как за отсчетные значения ответственны лишь неприливные фор-синги. Заметим в этой связи, что одних только данных наблюдений недоста-точно для оценивания отсчетных значений температуры и солености морской воды. Их нужно сначала подвергнуть воздействию процедур выявления скрытой периодичности или традиционного гармоничного анализа, затем необходимо устранить выделенную приливную гармонику. Имеется и другая возможность: привлечь результаты моделирования. Мы предпочли второй вариант. Поступая таким образом, получаем, что наблюдаемые и модельные значения переменных отличаются между собой не более чем на 0,1°С для температуры и 0,7‰ для солености, т. е. расхождения между ними приемлемы.
Отметим еще одну деталь: требуется понять причины появления сравни-тельно небольших модельных приливных изменений температуры и солено-сти морской воды. Среди них могут быть либо неизбежные ошибки оценива-ния отсчетных значений температуры и солености по результатам моделиро-вания, либо усреднение исходных полей по площади моря, приводящее к компенсации приливных изменений переменных с противоположными зна-ками, либо, наконец, нерепрезентативность найденных оценок приливных изменений температуры и солености в море Лаптевых по сравнению с пред-сказываемыми в других окраинных морях.
Сравнительно небольшие модельные значения приливных изменений температуры и солености морской воды, по всей видимости, суть следствия усреднения по площади моря, компенсирующего приливные изменения пе-ременных с противоположными знаками. В том, что это так, можно убедить-ся, обратившись к их максимальным значениям. Например, максимальное приливное изменение температуры (0,87°C) в придонном слое наблюдается в точке с координатами 73,97° с. ш., 109,92° в. д., тогда как максимальное приливное изменение солености в том же слое (–3,20‰) – в точке с коорди-натами 74,40° с. ш., 111,80° в. д. Здесь и ниже знаки приливных изменений полностью зависят от того, какова разность переменных, индуцируемых раз-ными форсингами: если она положительна или отрицательна, таким же будет знак приливного изменения температуры и солености. Далее, по сравнению с приведенными максимальными приливными изменениями температуры и солености в придонном слое в точке с координатами 73,97° с. ш., 109,92° в. д. локальные приливные изменения тех же переменных в поверхностном слое меньше (–0,12°C и 0,21‰ против 0,87°C и –2,75‰) по модулю. Ограничива-ясь рассмотрением только второй пары оценок как наибольших в том же смысле, мы видим, что в относительных единицах, нормированных на значе-ние этих переменных в придонном слое, локальные приливные изменения составляют ~ 100% для температуры и ~ 10% для солености и что, следова-тельно, прогнозы и расчеты экстремальных приливных изменений темпера-туры и солености в море можно усовершенствовать, учитывая эффекты ВПВ.
Заключение
Подведем итоги проделанной работы. С использованием высокоразре- шающей версии трехмерной конечно-элементной гидростатической модели QUODDY-4 воспроизведены приливные изменения модуля и направления результирующих скоростей постоянных течений в поверхностном и придонном слоях моря Лаптевых, температуры и солености морской воды там же, уровня свободной поверхности и вертикальных распределений приливных изменений температуры и солености вдоль меридионального разреза 120° в. д. Результаты моделирования показывают, что средние (за приливный цикл и пплощади моря) приливные изменения первых 9 климатических характеристик в море равны соответственно: –0,1 см/c и –0,4° в поверхностном слое; 0,0 см/c и –2,2° в придонном слое; –0,02 и 0,05°С для температуры и 0,10 и –0,20‰ для солености там же; –0,002 м – для уровня моря. Установлено также, что результаты моделирования свидетельствуют об усилении приливных изменений температуры и солености в придонном слое моря по сравнению с поверхностным. Этот факт подтверждается сравнением вертикальных профилей скорректированного (за счет эффектов ВПВ) и нескорректированного коэффициентов вертикальной турбулентной диффузии, определяемых, соот- ветственно, всеми рассматриваемыми форсингами, включая приливный. Оценивая средние (по площади моря) и экстремальные приливные изменения температуры и солености, убеждаемся, что общепринятое игнорирование приливных изменений температуры и солености морской воды оправдано лишь частично: оно справедливо для средних (по площади моря) значений и не справедливо для экстремальных. Последние применительно к морю Лаптевых составляют в относительных единицах ~ 100% для температуры и ~ 10% для солености. Это означает, что существующие сейчас методы прогноза и расчета экстремальных значений температуры и солености морской воды в части объема моря, равной ~ 40% от всего объема, в данном случае нуждаются в ревизии.

1. Kagan, B.A. and Sofina, E.V., 2017. A Method of Accounting for Tidal Changes in Regional Climates of a Water Basin under Conditions of an Ice-Free Barents Sea. Oceanology, 57(2), pp. 245-252. doihttps://doi.org/10.1134/S0001437016060047

2. Kagan, B.A., Sofina, E.V. and Timofeev, A.A., 2019. The Tidal Effect on Climatic Characteristics of the Kara Sea in the Ice-Free Period. Izvestiya, Atmospheric and Oceanic Physics, 55(2), pp. 188-195. doihttps://doi.org/10.1134/S0001433819020087

3. Jayne, S.R. and St. Laurent, L.C., 2001. Parameterizing Tidal Dissipation over Rough Topography. Geophysical Research Letters, 28(5), pp. 811-814. doihttps://doi.org/10.1029/2000GL012044

4. Osborn, T.R., 1980. Estimates of the Local Rate of Vertical Diffusion from Dissipation Measurements. Journal of Physical Oceanography, 10(1), pp. 83-89. doihttps://doi.org/10.1175/1520-0485(1980)010<0083:EOTLRO>2.0.CO;2

5. Zaslavsky, G.M. and Sagdeev, R.Z., 1988. Introduction to Nonlinear Physics. Moscow: Nauka, 368 p. (in Russian).

6. Ip, J.T.C. and Lynch, D.R., 1995. Comprehensive Coastal Circulation Simulation using Finite Elements: Nonlinear Prognostic Time-Stepping Model: QUODDY3 User's Manual. Hanover, New Hampshire, USA: Thayer School of Engineering, Dartmouth College, 45 p.

7. Lindsay, R., Wensnahan, M., Schweiger, A. and Zhang, J., 2014. Evaluation of Seven Different Atmospheric Reanalysis Products in the Arctic. Journal of Climate, 27(7), pp. 2588-2606. doihttps://doi.org/10.1175/JCLI-D-13-00014.1

8. Rio, M.H., Guinehut, S. and Larnicol, G., 2011. New CNES-CLS09 Global Mean Dynamic Topography Computed from the Combination of GRACE Data, Altimetry, and In Situ Measurements. Journal of Geophysical Research: Oceans, 116(C7), C07018. doihttps://doi.org/10.1029/2010JC006505

9. Jayne, S.R., 2009. The Impact of Abyssal Mixing Parameterizations in an Ocean General Circulation Model. Journal of Physical Oceanography, 39(7), pp. 1756- 1775. doihttps://doi.org/10.1175/2009JPO4085.1

10. Environmental Working Group, 1997. Environmental Working Group Joint U.S.- Russian Atlas of the Arctic Ocean, Version 1. Boulder, Colorado USA: NSIDC. doihttps://doi.org/10.7265/N5H12ZX4

11. Kagan, B.A. and Timofeev, A.A., 2020. The Determination of Baroclinic Tidal Energy Dissipation and Its Related Diapycnal Diffusivity as the First Step in Estimating the Role of Tidal Effects in the Formation of the Laptev Sea’s Climatic Characteristics. Fundamentalnaya i Prikladnaya Gidrofizika, 13(4), pp. 39-49 (in Russian). doihttps://doi.org/10.7868/S2073667320040048

12. Kozlov, I.E., Zubkova, E.V. and Kudryavtsev, V.N., 2017. Internal Solitary Waves in the Laptev Sea: First Results of Spaceborne SAR Observations. IEEE Geoscience and Remote Sensing Letters, 14(11), pp. 2047-2051. doihttps://doi.org/10.1109/LGRS.2017.2749681

13. Kagan, B.A. and Timofeev, A.A., 2020. High-Resolution Modeling of Semidiurnal Internal Tidal Waves in the Laptev Sea in the Ice-Free Period: Their Dynamics and Energetics. Izvestiya, Atmospheric and Oceanic Physics, 56(5), pp. 512-521. doihttps://doi.org/10.1134/S0001433820050047

14. Pingree, R.D. and New, A.L., 1995. Structure, Seasonal Development and Sunglint Spatial Coherence of the Internal Tide on the Celtic and Armorican Shelves and in the Bay of Biscay. Deep Sea Research Part I: Oceanographic Research Papers, 42(2), pp. 245-284. doihttps://doi.org/10.1016/0967-0637(94)00041-P

15. Hsu, M.-K., Liu, A.K. and Liu, C., 2000. A Study of Internal Waves in the China Seas and Yellow Sea Using SAR. Continental Shelf Research, 20(4-5), pp. 389-410. doihttps://doi.org/10.1016/S0278-4343(99)00078-3

16. Holloway, P.E., Chatwin, P.G. and Craig, P., 2001. Internal Tide Observations from the Australian North West Shelf in Summer 1995. Journal of Physical Oceanography, 31(5), pp. 1182-1199. doihttps://doi.org/10.1175/1520- 0485(2001)031<1182:ITOFTA>2.0.CO;2

17. Rainville, L. and Pinkel, R., 2006. Propagation of Low-Mode Internal Waves through the Ocean. Journal of Physical Oceanography, 36(6), pp. 1220-1236. doihttps://doi.org/10.1175/JPO2889.1

18. Vlasenko, V., Stashchuk, N., Hutter, K. and Sabinin, K., 2003. Nonlinear Internal Waves Forced by Tides near the Critical Latitude. Deep Sea Research Part I: Oceanographic Research Papers, 50(3), pp. 317-338. doihttps://doi.org/10.1016/S0967- 0637(03)00018-9