Purpose. The work is purposed at studying the vertical momentum transfer by internal waves at the exit from the Strait of Gibraltar to the Mediterranean Sea with due regard for turbulent viscosity and diffu-sion. Methods and Results. In contrast to the traditional approach relating vertical momentum transfer to small-scale turbulence, the present study examines the wave transport mechanism. The wave field is described by the classical equations of hydrodynamics for a stratified incompressible fluid with a shear flow with due regard for turbulent viscosity and diffusion. The boundary value problem for the ampli-tude of the vertical velocity of internal wave, which conditions the mode structure, is solved numerical-ly. In the linear approximation, its coefficients are complex that leads to a complex solution and, conse-quently, to a non-zero vertical wave momentum flux. The impact of horizontal turbulent viscosity and diffusion on this flux is investigated. Three models are compared: the first one – with the constant ex-change coefficients (basic case), the second – with the exchange coefficients depending on phenomenon scale according to the “4/3” law, and the third – with the coefficients of horizontal exchange taking into account stratification. It is shown that when the dependence of exchange coefficients on the phenome-non scale according to the “4/3” law is taken into account, the momentum flux is higher in magnitude than that with constant coefficients, but lower than the fluxes taking into account stratification. The same pattern holds for the vertical component of the Stokes drift velocity. The choice of exchange coefficients has virtually no effect on the horizontal component of the Stokes drift velocity. Conclusions. The dispersion curves of internal waves are independent of the choice of exchange coeffi-cients. However, the wave attenuation decrement is sensitive to this choice: it is higher in magnitude when the exchange coefficients depend on the phenomenon scale according to the “4/3” law as com-pared to the case of constant exchange coefficients, and even higher in absolute value when stratification is taken into account. The same pattern holds true for the vertical wave momentum flux.
internal waves, wave momentum flux, Stokes drift, turbulent viscosity, turbulent diffusion
Введение
Вертикальный перенос импульса обычно связывался с мелкомасштабной турбулентностью, которая генерируется под действием ветра и течений, а также вследствие обрушений поверхностных и внутренних волн [1–8]. Помимо обрушений внутренних волн следует указать на «мягкий» режим поддержания турбулентности, уже сгенерированной сдвигом скорости течения [9] во внутренней волне. Аналогично в сдвиговых течениях поток с числами Ричардсона, близкими к критическим, может не разрушаться и поддерживать турбулентность [10]. В придонном слое мелкомасштабная турбулентность может генерироваться в придонном пограничном слое в результате воздействия неоднородностей рельефа дна на течения и приливы [11]. Следует отметить захват трехмерной внутренней волны наклонным дном, когда угол наклона дна таков, что вектор групповой скорости отраженной волны параллелен дну. В этом случае энергия захваченной внутренней волны переходит в турбулентность [12].
В сдвиговых течениях на критических слоях, где скорость течения равна фазовой скорости внутренней волны, могут возникать вихревые структуры типа «кошачьих глаз» [13, 14]. Внутренние волны малых амплитуд затухают под воздействием мелкомасштабной турбулентности, волны больших амплитуд затухают незначительно, но способны усиливать турбулентность [15, 16]. При распространении внутренних волн в горизонтально-неоднородном океане в область малых глубин происходит увеличение их амплитуды с последующим проявлением нелинейных эффектов и диссипации энергии волны в турбулентность. Аналогичный механизм наблюдается в горизонтально-неоднородном волноводе: распространение внутренней волны приводит к ее захвату и фокусировке с последующей диссипацией энергии в турбулентность [17]. Внутренние волны нередко распространяются в виде волновых пакетов [18, 19]. При распространении пакетов слабонелинейных внутренних волн генерируются средние течения, являющиеся эффектом второго порядка малости по амплитуде волны [20, 21]. На переднем и заднем фронтах волнового пакета вертикальная компонента скорости этого индуцированного течения имеет противоположные знаки, поэтому переноса по вертикали не происходит.
Внутренние волны даже без обрушений могут вносить вклад в вертикальный обмен. В диссипативной среде с учетом вязкости и диффузии внутренние волны затухают [22–24]. Фазовый сдвиг между колебаниями вертикальной и горизонтальной скоростей при учете турбулентной вязкости и диффузии отличен от 
и приводит к значениям вертикального волнового потока импульса, отличным от нуля [25–31]. Это обусловлено тем, что уравнение для собственной функции внутренних волн содержит комплексные коэффициенты, а решение соответствующей краевой задачи – комплексное [32, 33], при этом частота волны имеет малую мнимую часть [34–39]. До недавнего времени считалось, что коэффициенты горизонтального турбулентного обмена постоянны и не зависят от масштаба явления [27–31]. В работе [26] учитывалась зависимость коэффициента горизонтального турбулентного обмена от масштаба явления по закону «4/3» , :
при постоянной частоте плавучести.
В настоящей работе рассматриваются реальные профили стратификации и течения по данным натурного эксперимента на выходе из Гибралтарского пролива в сторону Средиземного моря, учитывается зависимость коэффициента горизонтального обмена от масштаба явления по закону «4/3», однако коэффициент 
пропорциональности в этом законе связывается с частотой Брента – Вяйсяля. Основанием для этого служат данные дрифтерного эксперимента, приведенные в работах [40, 41]. Согласно этим данным, коэффициент горизонтального обмена пропорционален произведению масштаба скорости 
и масштаба длины L. Масштаб длины пропорционален бароклинному радиусу деформации Россби, который пропорционален средней по глубине частоте плавучести
Целью настоящей работы является определение вертикального волнового потока импульса у внутренних волн при зависимости коэффициентов горизонтального обмена от масштаба явления по закону «4/3» и частоты плавучести.
Постановка задачи
В приближении Буссинеска рассматриваются свободные прогрессивные внутренние волны в безграничном море постоянной глубины при наличии сдвигового течения [25–31]. Если ранее коэффициенты горизонтального турбулентного обмена предполагались постоянными [25–31], то в настоящей работе они зависят от вертикальной координаты и горизонтального масштаба явления. В линейном приближении находятся амплитудные и дисперсионные характеристики внутренних волн, во втором порядке по амплитуде волны определяются вертикальный волновой поток импульса и компоненты скорости стоксова дрейфа [25–27].
Система уравнений гидродинамики для волновых возмущений имеет следующий вид [25–31]:
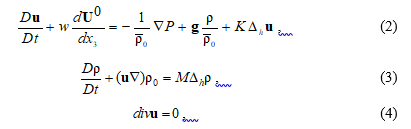
где 
– вектор волновых возмущений скорости течения; ось 
декартовой трехмерной системы координат направлена вдоль среднего плоскопараллельного течения, ось 
направлена противоположно вектору ускорения свободного падения 
; 
– вектор скорости среднего течения; 
, 
– волновые возмущения плотности и давления [25–39]; 
– невозмущенная средняя плотность; 
– коэффициенты горизонтальной турбулентной вязкости и диффузии; действие оператора раскрывается как [25–39]. Граничные условия на поверхности и на дне: условия «твердой крышки» [22, 25–39] и условие «гладкого скольжения» [23, 25–31].
Линейное приближение. Решения линейного приближения для прогрессивной волны имеют следующий вид [25–39]:
Подстановка формулы (5) в систему (2)–(4) приводит к системе уравнений, связывающей амплитудные функции 
с 
[25–31]:
.
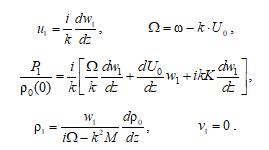
Амплитудная функция вертикальной скорости 
удовлетворяет уравнению
, ,
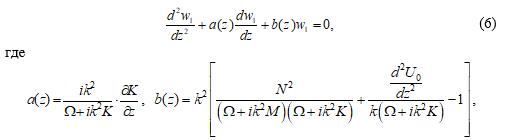
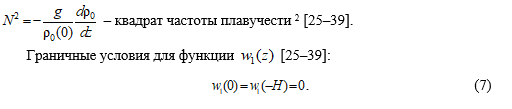
Нелинейные эффекты. Две компоненты скорости стоксова дрейфа определяются по формулам [42, 25–31])
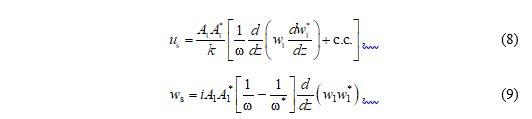
где 
, 
. Учет турбулентной вязкости и диффузии приводит к тому, что частота волны имеет малую мнимую часть и вертикальная составляющая скорости стоксова дрейфа (9) не равна нулю [25–31]. Влияние турбулентной вязкости и диффузии на горизонтальную компоненту скорости стоксова дрейфа (8) рассматривается ниже.
Вертикальный волновой поток импульса 
определяется по формуле 2 [25–27, 29, 31–35, 38]
. 
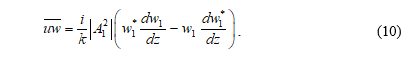
Решение краевой задачи (6), (7) – комплексное, поэтому поток импульса (10) отличен от нуля.
Результаты расчетов и их анализ
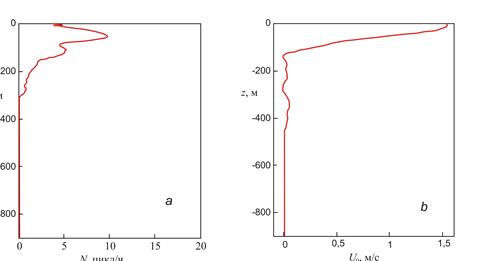
Для расчета вертикального волнового потока импульса используем данные натурного эксперимента в Гибралтарском проливе [43]. На полигоне эксперимента как дистанционными методами, так и с помощью контактных измерений регистрировали интенсивные внутренние волны с амплитудой до 16 м. Была выявлена первая мода с периодом 14 мин, причем оценка фазовой скорости по данным измерений и теоретические расчеты с помощью численного решения уравнения Тейлора – Гольдштейна для профилей скорости течения и частоты плавучести (рис. 1) продемонстрировали хорошее согласие [43].
Ранее нами предполагалось, что на рассматриваемых масштабах 
. В настоящей работе учитывается зависимость коэффициента горизонтального турбулентного обмена от масштаба явления и частоты Брента – Вяйсяля. Отметим, что стратификация препятствует вертикальному обмену и подавляет мелкомасштабную турбулентность, однако не препятствует горизонтальному обмену, а, напротив, даже усиливает его [44]. На это указывают данные натурного эксперимента по определению коэффициентов горизонтального турбулентного обмена [45]. Полученные вертикальные распределения этого коэффициента указывают на его увеличение в области пикноклина при отсутствии циклонов. Поэтому применим модифицированную формулу Райли [44]
,
где 
– коэффициент горизонтального турбулентного обмена в однородной жидкости, зависящий от масштаба явления l по закону «4/3»:
, 
здесь коэффициент 
по данным измерений в большом бассейне равен 
(согласно работе 3). Из формул (11), (12) находим коэффициент горизонтального турбулентного обмена при наличии стратификации:
.
|
|
|
|
Р и с. 1. Зависимость частоты плавучести (а) и скорости течения (b) от вертикальной координаты F i g. 1. Dependence of buoyancy frequency (a) and current velocity (b) on the vertical coordinate |
|
Здесь 
– частота Брента – Вяйсяля, цикл/ч, 
цикл/ч. Такое значение 
обеспечивает попадание эмпирических значений коэффициента 
(см. работу 3 и [46]) в законе «4/3» (1) в интервал изменения функции 
. Под масштабом явления в формулах (1), (13) будем понимать длину волны, т. е. 
. Краевая задача (6), (7) решается численно по неявной схеме Адамса второго порядка при 
[26]. Для фиксированной действительной части частоты волны 
волновое число и декремент затухания волны находятся методом пристрелки 2 [25–31, 34–39]. Сравниваются результаты расчетов с коэффициентом турбулентного обмена – фиксированным () и зависящим от масштаба явления по закону «4/3», как при постоянном значении 
в формуле (1), так и в случае зависимости (формула (13)) коэффициента обмена от стратификации.
На рис. 2 представлены дисперсионные кривые первой моды для этих трех случаев. Дисперсионные кривые почти совпадают, т. е. действительная часть частоты нечувствительна к зависимости (1) коэффициента обмена от масштаба l и зависимости (13) коэффициента обмена от частоты плавучести. Зато мнимая часть частоты волны заметно зависит от выбора коэффициента горизонтального турбулентного обмена (рис. 3).
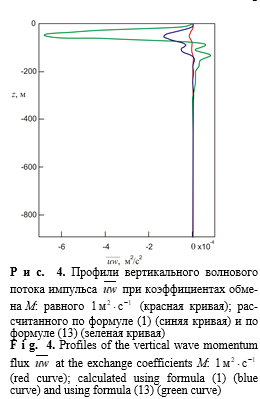
Аналогичные расчеты для трех вариантов выбора коэффициента турбулентного обмена выполнены для вертикального волнового потока импульса 
(10) у 14-минутных внутренних волн первой моды (рис. 4).
В варианте 2, когда коэффициент турбулентного обмена зависит от масштаба явления по формуле (1), вертикальный волновой поток импульса заметно выше по абсолютной величине, чем в варианте 1, при 
, и меньше по модулю потока импульса в варианте 3. Аналогичным образом выполнены и расчеты для двух компонент скорости стоксова дрейфа для рассматриваемых трех вариантов выбора коэффициентов турбулентного обмена (рис. 5, 6).
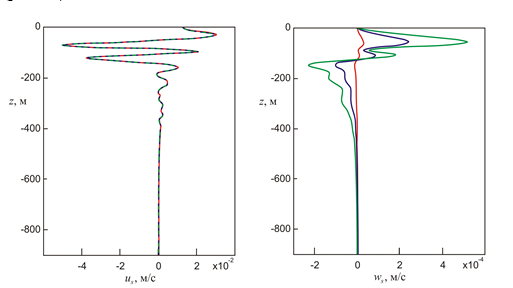
Как видим, выбор коэффициента обмена почти не влияет на горизонтальную компоненту скорости стоксова дрейфа (8). На рис. 6 представлены результаты расчета вертикальной составляющей скорости стоксова дрейфа (9). Эта компонента скорости в варианте 1 выбора коэффициентов обмена по модулю меньше, чем в варианте 2, а в последнем, в свою очередь, меньше, чем в варианте 3.
Заключение
Вертикальный волновой поток импульса у внутренних волн при учете горизонтальной турбулентной вязкости и диффузии отличен от нуля. Это связано с тем, что уравнение для амплитуды вертикальной скорости содержит комплексные коэффициенты и решение краевой задачи (6), (7) – комплексное. Частота волны комплексная и имеет малую мнимую часть – декремент затухания волны, который находится в ходе решения этой краевой задачи. Между компонентами волновых возмущений скорости существует сдвиг фаз, отличный от 
, что приводит к отличному от нуля значению вертикального волнового потока импульса. При постоянном коэффициенте турбулентного обмена 
вертикальный волновой поток импульса заметно меньше по модулю, чем при коэффициенте обмена, зависящем от масштаба явления по формуле (1). В свою очередь, в последнем случае поток импульса заметно меньше по абсолютной величине, чем при коэффициенте обмена, задаваемом формулой (13), учитывающей стратификацию. На дисперсионных кривых выбор коэффициента обмена почти не сказывается, однако декремент затухания волны чувствителен к этому выбору. Декремент затухания волны при 
по модулю наименьший, Он увеличивается в случае, когда коэффициент обмена определяется по формуле (1), и становится наибольшим по абсолютной величине при расчете по формуле (13) при постоянном волновом числе. Горизонтальная компонента скорости стоксова дрейфа почти не зависит от выбора коэффициента турбулентного обмена, в то время как вертикальная компонента заметно выше по абсолютной величине, когда коэффициент турбулентного обмена зависит от масштаба явления по формуле (1), по сравнению с вариантом, когда постоянный коэффициент обмена
. Зависимость (13), учитывающая влияние стратификации на коэффициент вертикального турбулентного обмена, дополнительно увеличивает вертикальную компоненту скорости стоксова дрейфа. Вертикальная компонента скорости стоксова дрейфа играет существенную роль в вертикальном переносе тепла и соли.
1. Ozmidov R. V. O turbulentnom obmene v ustoychivo stratificirovannom okeane // Izve-stiya AN SSSR. Fizika atmosfery i okeana. 1965. T. 1, № 8. S. 853–860.
2. Wunsch C., Ferrari R. Vertical mixing, energy, and the general circulation of the ocean // An-nual Review of Fluid Mechanics. 2004. Vol. 36, iss. 1. P. 281–314. https://doi.org/10.1146/annurev.fluid.36.050802.122121
3. Holford J. M., Linden P. F. Turbulent mixing in a stratified fluid // Dynamics of Atmosphere and Oceans. 1999. Vol. 30, iss. 2–4. P. 173–198. https://doi.org/10.1016/S0377-0265(99)00025-1
4. Samodurov A. S., Lyubickiy A. A., Panteleev N. A. Vklad oprokidyvayuschihsya vnutren-nih voln v strukturoobrazovanie, dissipaciyu energii i vertikal'nuyu diffuziyu v okeane // Morskoy gidrofizicheskiy zhurnal. 1994. № 3. S. 14–27.
5. Podymov O. I., Zacepin A. G., Ostrovskiy A. G. Vertikal'nyy turbulentnyy obmen v chernomorskom piknokline i ego svyaz' s dinamikoy vod // Okeanologiya. 2017. T. 57, № 4. S. 546–559. EDN ZCRXXJ. https://doi.org/10.7868/S0030157417040049
6. Ohotnikov I. N., Panteleev N. A. Sdvigovaya neustoychivost' vnutrennih voln i verti-kal'nyy obmen v okeane // Morskoy gidrofizicheskiy zhurnal. 1985. № 3. S. 13–20.
7. Desabies Y., Smith W. K. Statistics of Richardson number and instability in oceanic internal waves // Journal of Physical Oceanography. 1982. Vol. 12, № 11. P. 1245–1269. https://doi.org/10.1175/1520-0485(1982)012<1245:SORNAI>2.0.CO;2
8. Vliyanie dinamiki techeniy na gidrologicheskuyu strukturu vod i vertikal'nyy obmen v deyatel'nom sloe Chernogo morya / A. G. Zacepin [i dr.] // Okeanologiya. 2007. T. 47, № 3. S. 327–339. EDN IAFSJJ.
9. Interaction of internal waves and turbulense in the upper layer of the ocean / A. V. Ivanov [et al.] // Dynamics of Atmosheres and Ocean. 1984. Vol. 7, № 4. P. 221–232. EDN XMUZZM. https://doi.org/10.1016/0377-0265(83)90006-4
10. Prostoe opisanie turbulentnogo perenosa v stratificirovannom sdvigovom potoke primenitel'no k opisaniyu termogidrodinamiki vnutrennih vodoemov / I. A. Soustova [i dr.] // Izvestiya RAN. Fizika atmosfery i okeana. 2020. T. 56, № 6. S. 689–699. EDN FCUZWC. https://doi.org/10.31857/S0002351520060103
11. Itsweire E. C., Helland K. N., Van Atta C. W. The evolution of grid-generated turbulence in a stably stratified fluid // Journal of Fluid Mechanic. 1986. Vol. 162, iss. 2. P. 299–338. https://doi.org/10.1017/S0022112086002069
12. Role of internal waves in the generation of nepheloid layers on the northwestern Alboran slope: Implication for continental margin shaping / P. Puig [et al.] // Journal of Geophysical Research. 2004. Vol. 109, iss. C9. C09011. https://doi.org/10.1029/2004JC002394
13. Kelly R. E., Maslowe S. A. The non-linear critical layer in a slightly stratified shear flow // Stud-ies in Applied Mathematics. 1970. Vol. 49, iss. 4. P. 301–326.
14. Robinson J. L. The inviscid nonlinear instability of parallel shear flows // Journal of Fluid Me-chanics. 1974. Vol. 63, iss. 4. P. 723–752.
15. Ostrovsky L. A., Zaborskikh D. V. Damping of internal gravity waves by small-scale turbulence // Journal of Physical Oceanography. 1996. Vol. 26, iss. 3. P. 388–397.
16. Druzhinin O. A., Ostrovsky L. A. Dynamics of turbulence under the effect stratification and internal waves // Nonlinear Processes in Geophysics. 2015. Vol. 22, iss. 3. P. 337–348. https://doi.org/10.5194/npg-22-337-2015
17. Badulin S. I., Cimring L. Sh., kotoraya Shrira komponent V. I. Zahvat i vertikal'naya zdes' fokusirovka vnut-rennih voln v stratif piknokline lineynoe gorizontal'nymi neodnorodnostyami nenie stratifikacii i techeniy // zondirovaniy Doklady shel'fe AN SSSR. 1983. T. 273, № 2. S. 459–463.
18. Bulatov V. V., Vladimirov Yu. V. Volny v stratificirovannyh sredah. Moskva : Nauka, 2015. 735 s.
19. Vnutrennie volny v rayone Gerakleyskogo poluostrova: modelirovanie i nablyude-nie / V. A. Ivanov [i dr.] // Morskoy gidrofizicheskiy zhurnal. 2019. T. 35, № 4. S. 322–340. EDN SOBBLG. https://doi.org/10.22449/0233-7584-2019-4-322-340
20. K teorii nestacionarnyh slabonelineynyh vnutrennih voln v stratificirovannoy zhidkosti / Yu. D. Borisenko [i dr.] // Izvestiya AN SSSR. Fizika atmosfery i okeana. I976. T. 12, № 3. S. 293–301.
21. Grimshaw R. The modulation of an internal gravity wave packet and the resonance with the mean motion // Studies in Applied Mathematics. 1977. Vol. 56, iss. 3. R. 241–266. https://doi.org/10.1002/sapm1977563241
22. Le Blon P., Maysek L. Volny v okeane. Moskva : Mir, 1981. Ch. 2. 365 s.
23. Le Blond P. H. On damping of internal gravity waves in a continuously stratified ocean // Jour-nal of Fluid Mechanics. 1966. Vol. 25, iss. 1. R. 121–142. https://doi.org/10.1017/S0022112066000089
24. Ostrovskiy L. A., Soustova I. A. Verhniy peremeshannyy sloy kak stok energii vnut-rennih voln // Okeanologiya. 1979. T. 19, vyp. 6. S. 973–981.
25. Slepyshev A. A. Vertikal'nye perenos impul'sa vnutrennimi volnami pri uchete turbu-lentnoy vyazkosti i diffuzii // Izvestiya RAN. Fizika atmosfery i okeana. 2016. T. 52, № 3. S. 342–350. EDN WALSFX. https://doi.org/10.7868/S0002351516030111
26. Slepyshev A. A. Vertikal'nyy perenos impul'sa vnutrennimi volnami v sdvigovom potoke pri uchete turbulentnoy vyazkosti i diffuzii // Izvestiya RAN. Fizika atmosfe-ry i okeana. 2022. T. 58, № 5. S. 504–511. EDN OSUVED. https://doi.org/10.31857/S000235152205011X
27. Slepyshev A. A., Nosova A. V. Vertikal'nyy perenos impul'sa vnutrennimi volnami v zapadnoy chasti Sredizemnogo morya // Morskoy gidrofizicheskiy zhurnal. 2022. T. 38, № 4. S. 358–371. EDN XJNRJF. https://doi.org/10.22449/0233-7584-2022-4-358-371
28. Slepyshev A. A. Generaciya vertikal'noy tonkoy struktury vnutrennimi volnami na morskom shel'fe // Izvestiya RAN. Mehanika zhidkosti i gaza. 2023. № 3. S. 111–124. EDN TMNYOX. https://doi.org/10.31857/S1024708422600749
29. Slepyshev A. A. Vertikal'nyy perenos impul'sa inercionno-gravitacionnymi vnutren-nimi volnami na techenii pri uchete turbulentnoy vyazkosti i diffuzii // Izvestiya RAN. Mehanika zhidkosti i gaza. 2022. № 2. S. 77–86. EDN OYOVJK. https://doi.org/10.31857/S0568528122020098
30. Slepyshev A. A., Nosova A. V. Generaciya vertikal'noy tonkoy struktury vnutrennimi volnami pri uchete turbulentnoy vyazkosti i diffuzii // Morskoy gidrofizicheskiy zhurnal. 2020, T. 36, № 1. S. 5–19. EDN IZIVIK. https://doi.org/10.22449/0233-7584-2020-1-5-19
31. Slepyshev A. A. Vertikal'nye potoki, obuslovlennye slabonelineynymi vnutrennimi volnami v baroklinnom techenii // Morskoy gidrofizicheskiy zhurnal. 2015. № 1. S. 64–78. EDN VBUSQD.
32. Slepyshev A. A., Laktionova N. V. Vertikal'nyy perenos impul'sa vnutrennimi volna-mi v sdvigovom potoke // Izvestiya RAN. Fizika atmosfery i okeana. 2019. T. 55, № 6. S. 194–200. EDN ZDIYNQ. https://doi.org/10.31857/S0002-3515556194-200
33. Slepyshev A. A., Shadt M. A. Vliyanie netradicionnogo priblizheniya na perenos impul'-sa vnutrennimi volnami v sdvigovom potoke // Izvestiya RAN. Fizika atmosfery i oke-ana. 2024. T. 60, № 5. S. 601–610. EDN HYEKQK. https://doi.org/10.31857/S0002351524050035
34. Slepyshev A. A. Vertikal'nyy perenos impul'sa inercionno-gravitacionnymi vnutren-nimi volnami na dvumernom sdvigovom techenii // Morskoy gidrofizicheskiy zhurnal. 2021. T. 37, № 4. S. 279–287.
35. Ankudinov N. O., Slepyshev A. A. Vertikal'nyy perenos impul'sa v dvumernom potoke // Izvestiya RAN. Mehanika zhidkosti i gaza. 2021. № 3. S. 39–47. EDN UADMVN. https://doi.org/10.31857/S0568528121030026
36. Slepyshev A. A., Vorotnikov D. I. Vertikal'nye potoki tepla i soli, obuslovlennye inercionno-gravitacionnymi vnutrennimi volnami na morskom shel'fe // Izvestiya RAN. Fizika atmosfery i okeana. 2017. T. 53, № 4. S. 532–541. EDN ZBPXRX. https://doi.org/10.7868/S0003351517040110
37. Bagatinskiy V. A., Slepyshev A. A. Vertikal'nyy perenos impul'sa slabonelineynymi inercionno-gravitacionnymi vnutrennimi volnami // Izvestiya RAN. Mehanika zhidko-sti i gaza. 2016. № 5. S. 17–28. EDN WRJJGL. https://doi.org/10.7868/S0568528116050042
38. Slepyshev A. A., Ankudinov N. O. Generaciya vertikal'noy tonkoy struktury vnutrenni-mi volnami na sdvigovom techenii // Morskoy gidrofizicheskiy zhurnal. 2024. T. 40, № 2. S. 180–197. EDN HTYLSO.
39. Slepyshev A. A., Vorotnikov D. I. Generation of Vertical Fine Structure by internal waves in a Shear Flow // Open Journal of Fluid Dynamics. 2019. Vol. 9. P. 140–157. https://doi.org/10.4236/ojfd.201992010
40. Zhurbas V., Oh I. S. Lateral diffusivity and Lagrangian scales in the Pacific ocean as derived from drift data // Journal of Geophysical Research: Oceans. 2003. Vol. 108, iss. S5. 3141. https://doi.org/10.1029/2002JC001596
41. Cirkulyaciya vod i harakteristiki raznomasshtabnyh techeniy v verhnem sloe Chernogo morya po drifternym dannym / V. M. Zhurbas [i dr.] // Okeanologiya. 2004. T. 44, № 1. S. 34–48. EDN OWJSRJ.
42. Longuet-Higgins M. S. On the transport of mass by time varying ocean current // Deep-Sea Research. Vol. 16, iss. 5. P. 431–447. https://doi.org/10.1016/0011-7471(69)90031-X
43. Watson G. Internal waves in a stratified shear flow: the Strait of Gibraltar // Journal of Physical Oceanography. 1994. Vol. 24, iss. 2. P. 509–517. https://doi.org/10.1175/1520-0485(1994)024<0509:IWIASS>2.0.CO;2
44. Riley G. Parameters of turbulence in the sea // Journal of Marine Research. 1951. Vol. 10, iss. 3. P. 267–287.
45. Permyakov M. S., Tarhova T. I., Sergienko A. S. Ocenka gorizontal'nyh koefficientov turbulentnogo obmena v severo-zapadnoy chasti Tihogo okeana // Issledovano v Rossii. 2005. T. 8. S. 860–869. EDN MESHKZ. URL: http://zhurnal.ape.relan.ru/articles/2005/082.pdf (data obrascheniya: 20.09.2025).
46. Nemchenko V. I. Issledovanie gorizontal'noy turbulentnoy diffuzii v Atlanticheskom okeane // Okeanologiya. 1964. T. 4, vyp. 5. S. 805–808.
