Введение

Речной сток является главным источником притока в моря пресных вод, содержащих растворенные вещества, взвеси и продукты антропогенной деятельности континентального происхождения, многие из которых оказывают негативное воздействие на морскую экологию. В области впадения речных вод в море формируются плюм (опресненная водная масса, образующаяся в результате перемешивания речного стока и соленых морских вод) и вдольбереговое плотностное течение, которые, в свою очередь, воздействуют на динамические процессы в прибрежной зоне. Поэтому изучение распространения речных вод на морских шельфах – важная фундаментальная и прикладная задача [1–4]. Речные плюмы, формирующиеся в прибрежных морских акваториях во многих регионах мира, обычно представляют собой большой по площади, но тонкий поверхностный слой моря, который, благодаря градиенту плотности, обособлен от подстилающих морских вод [4, 5].

Исследование возникновения и эволюции речных плюмов основано на анализе контактных и спутниковых измерений [5–11], лабораторных экспериментов [12, 13] и численного моделирования [13–18]. Динамика вод шельфа определяется процессами разных пространственно-временны́х масштабов, таких как геострофические течения, фронтальные зоны, перемешивание водных масс, апвеллинги/даунвеллинги, волновые явления и приливы. В свою очередь, формирование речного плюма и связанного с ним вдольберегового плотностного течения зависит от множества факторов: геометрии устья, топографии дна, характеристик речного стока, параметра Кориолиса, ветрового воздействия, приливов, придонного трения. Эти процессы также влияют на прибрежную динамику вод шельфа [6–10].

При отсутствии внешних воздействий (ветра, приливов) речные воды образуют линзу распресненных вод, которая ограничена гидрофронтом. Для рассматриваемого района его граница выделяется по изохалине 16 ЕПС [11]. Характерные масштабы линзы как ядра плюма – ширина и глубина – определяются плотностью вод реки и шельфа, параметром Кориолиса и скоростью втока реки, которая вычисляется из величин расхода воды, ширины и глубины устья [7, 8, 12]. В зависимости от характерных масштабов плюма и топографии дна выделяют разные типы плюмов: придонный, промежуточный и поверхностный [9]. В статье рассматривается поверхностный тип плюма.

Для Черного моря в условиях отсутствия приливного перемешивания и ветрового воздействия поверхностный плюм таких рек, как Дунай и Днестр, приобретает характерную форму «свободного плюма». Он состоит из линзы распресненной воды в приустьевой области, ограниченной гидрофронтом, которая представляет собой ядро плюма (англ. bulge), и вдольберегового течения. В квазистационарном состоянии ядро плюма является антициклоническим вихрем, что обусловлено циклострофическим балансом [9, 13]. Вдольбереговое течение развивается в антициклоническом направлении от устья как квазигеострофическое компенсационное течение [10]. Свободный плюм служит идеальным объектом для валидации численных моделей и оценки масштабов плюма по данным контактных и дистанционных измерений в условиях слабых ветров [14–17]. На основе численного моделирования на сезонных масштабах в районе устья Дуная было установлено наличие антициклонического круговорота, формирующегося в результате весеннего паводка рек в отсутствие ветрового воздействия [18]. Затем с учетом сезонной изменчивости речного стока и поля ветра в результате численного моделирования были получены карты пространственного распределения вод с пониженной соленостью от устьев рек в прибрежных областях северо-западного шельфа Черного моря (СЗШЧМ) [14]. Учет комбинации указанных факторов с влиянием топографии дна позволил смоделировать характерные пути распространения распресненных вод на СЗШЧМ на сезонном [19] и межгодовом масштабах [17].

Хотя приведенные исследования демонстрируют значительное влияние ветра на пути распространения речных вод на СЗШЧМ, процессы плавучести, перемешивания, инерции играют важную роль на ранних стадиях формирования плюма и вдольберегового течения. Эти процессы определяют перенос распресненных вод и, соответственно, взвешенных и растворенных веществ в прибрежной зоне шельфа [15, 20]. В связи с этим требуют уточнения механизмы формирования ядра плюма и установления квазистационарного вдольберегового течения, необходимы количественные оценки перераспределения речной воды между плюмом и течением в зависимости от гидрологических характеристик вод СЗШЧМ, параметризация радиуса плюма на основе его завихренности и глубины.

Таким образом, целью данной работы является изучение распространения речных вод при впадении в море, формирования плюма и вдольберегового плотностного течения, оценка характеристик плюма и его пространственно-временно́й эволюции в зависимости от расхода реки, геометрии устья, различных физических параметров и гидрологических условий северо-западного шельфа Черного моря в отсутствие ветрового воздействия.

Район исследования

Для СЗШЧМ характерен обширный мелководный шельф: изобата 50 м расположена на расстоянии 50–200 км от береговой линии. Примерно 80 % общего объема речного стока, поступающего в Черное море, приходится на долю рек Днепр, Южный Буг, Днестр и Дунай, впадающих в акваторию шельфа [21]. На гидрологическую структуру вод этого района сильное влияние оказывают изменчивость ветрового режима, выхолаживание и летний прогрев прибрежных областей, колебания стока рек [21, 22].

Самой крупной из рек, впадающих в Черное море, является река Дунай – вторая по величине река Европы, средний многолетний расход воды которой равен 200 км³, что составляет 57,5 % от общего стока рек в Черное море, а расход наносов с учетом регулирования достигает 30 мл м³ [23]. Воды Дуная образуют обширный плюм и развитое прибрежное течение (рис. 1), которые также оказывают значительное влияние на экологическое состояние вод шельфа и сезонный цикл концентрации хлорофилла а [24].

Горизонтальный и вертикальный масштабы плюма и величина расхода прибрежного течения зависят от сезонного хода стока рек, плотности втекающей воды и вод шельфа, параметра Кориолиса, геометрии устья. Сезонная изменчивость стока рек значительна: максимальный сток за 1985–2006 гг. у Дуная (9530 м³/с) наблюдается в апреле, у Днепра (1798 м³/с) в мае, а минимальный – у Дуная (4700 м³/с) в сентябре, у Днепра (724 м³/с) в августе [23]. У Дуная обширная дельта, но в основном приток воды в море происходит через три основных рукава: Килийский (до 63 % основного стока), Сулинский (17 %) и Георгиевский (20 %) [25].

Р и с.  1. Регион Черного моря (справа), прямоугольным контуром выделен район исследования; увеличенное изображение района исследования (слева) с плюмом в районе дельты Дуная 01.04.2017, по спутниковым данным (длина волны 0,551 мкм) (URL: http://dvs.net.ru/mp)

F i g.  1. Black Sea region (right), the study area is outlined by a rectangular circuit; enlarged image of the study area (left) with a plume in the Danube Delta region on 01.04.2017 based on satellite data (wavelength 0.551 μm) (URL: http://dvs.net.ru/mp)

Исходные данные и методы исследования

Структура речного плюма включает в себя источник пресной воды c расходом Q_r, устье шириной L и глубиной h₀ и область транзита речных вод. Область смешения речных и морских вод включает гидрофронт, сформированный в результате распространения речных вод в виде антициклонического круговорота (в Северном полушарии) с радиусом r и область вдольберегового плотностного течения шириной W_p (рис. 2). Внутренняя граница зоны смешения речных и морских вод для условий СЗШЧМ и стока Дуная находится в среднем на расстоянии 0–4 км от устьев рукавов, что примерно соответствует инерционному масштабу L₀ = U₀/f, где U₀ – скорость втекания реки; f – параметр Кориолиса. Внешняя граница зоны смешения определяется по положению перегиба на профиле изохалин, за которым градиент солености уменьшается, а ее значение приближается к фоновой солености вод шельфа. Для СЗШЧМ соленость воды на внешней границе зоны смешения составляет ~ 16 ЕПС, что соответствует ~ 90 % от солености вод открытой части Черного моря [11].

Пресная вода втекает на шельф со скоростью, определяемой расходом реки и геометрией устья, U₀ = Q_r/h₀L (рис. 2) при условии, что река впадает в море под прямым углом и характеризуется гидродинамическим режимом с числом Фруда Fr = U₀/C₀, где C₀ = (g'h₀)^1/2 – фазовая скорость гравитационной волны; g' = g(ρ_o − ρ_a)/ρ₀ – приведенное ускорение свободного падения; ρ₀, ρ_a – плотность речной и морской воды. Случаи, когда река образует эстуарий, соединенный с морем, в данной работе не рассматриваются.

Вблизи устья (ближняя зона), как правило, Fr < 1 и динамика плюма определяется инерцией и стратификацией. В точке отрыва (О) при Fr = 1 плюм отрывается от дна и распространяется в поверхностном слое толщиной h_p – это область ускорения потока и интенсивного перемешивания вследствие сдвиговой неустойчивости и крупномасштабных процессов перемешивания (зона А). Далее следует зона В – область потока с максимальными значениями Fr, превышающими 1, где происходит интенсивное перемешивание в процессе распространения плюма. Завершает эволюцию зона C – область распространения плюма и постепенного уменьшения числа Fr вплоть до внешней морской границы (рис. 2). В табл. 1 представлены характеристики речных плюмов для разных рек и типов шельфа, полученные по гидрологическим данным [15, 16, 26–27].

Р и с.  2. Схема формирования плюма и циркуляции вод в устье реки: a – вид сверху; b – фронтальный разрез. Обозначения: L – ширина устья; r – радиус плюма; Wp – ширина прибрежного течения; Q_r – расход реки; h₀ – глубина устья; U₀ – скорость втока реки; ρ₀ – плотность речной воды; x_b – ширина плюма; U – скорость плюма; h_p – глубина плюма; ρ_a – плотность морских вод; О – точка отрыва плюма от дна при Fr = 1; A – область ускорения потока и интенсивного перемешивания, B – область интенсивного перемешивания потока, C – область распространения плюма

F i g.  2. Schematic diagram of formation of plume and water circulation in the river mouth: a – top view; b – frontal section. Designations: L – mouth width; r – plume radius; Wp – coastal current width; Q_r – river discharge; h₀ – mouth depth; U₀ – river inflow velocity; ρ₀ – river water density; x_b – plume width; U – plume velocity; h_p – plume depth; ρ_a – seawater density; O – point of plume detachment from the bottom at Fr = 1; A – area of flow acceleration and intense mixing, B – area of intense flow mixing, C – area of plume spread

Т а б л и ц  а 1

T a b l e  1

Характеристики речных плюмов

Characteristics of river plumes

П р и м е ч а н и е. Обозначения: Q_r – расход реки, м³/с; h_p – толщина плюма, м; H_R – глубина дна, м, для x = R_di; W_sh – ширина шельфа, км; α – уклон дна; R_di – бароклинный радиус Россби, км.

N o t e. Designations: Q_r is river discharge, m³/s; h_p is plume thickness, m; H_R is bottom depth, m, for x = R_di; W_sh is shelf width, km; α is bottom slope; R_di is baroclinic Rossby radius, km.

Отношение толщины плюма h_p к глубине дна H_R на расстоянии от берега, равном бароклинному радиусу Россби R_d, характеризует тип плюма: при h_p/Н_R < 1 плюм поверхностный, при h_p/Н_R > 1 – придонный, при h_p/Н_R = 1 плюм занимает промежуточное положение [16]. Реки, представленные в табл. 1, формируют поверхностный плюм, а плюм Дуная сопоставим по параметрам, например, с плюмом Миссисипи. Следует отметить, что для Черного моря значение g' в среднем больше, чем для шельфа океана на той же широте, что приводит к бόльшим значениям горизонтального и меньшим значениям вертикального масштабов плюма при одинаковых расходах рек.

Горизонтальный масштаб и глубина плюма зависят от стратификации вод шельфа и расхода воды реки, сезонная изменчивость которых влияет на внутренний радиус Россби R_d: разница значений R_d между июлем и январем достигает 2,5 км для СЗШЧМ [25]. R_d достигает максимального значения летом: в глубоководной части моря – 20 км, на СЗШЧМ – до 12,5 км, а на шельфе глубиной менее 100 м находится в пределах 3,0–7,5 км и имеет тенденцию к уменьшению с увеличением широты [25].

Поверхностный плюм и прибрежное течение находятся с кросс-шельфовым градиентом давления в геострофическом балансе, который устанавливается через 2–3 инерционных периода после втекания речной воды. Соответственно, используя геострофические соотношения, толщину плюма можно представить в виде

hp =(2Qrf/g')1/2,                                              (1)

бароклинный радиус Россби с учетом выражения (1) в таком случае равен [13]

Rd=(2Qrg'/f3)1/4.                                             (2)

Таким образом, наряду с инерционным масштабом L₀ и бароклинным радиусом Россби для иследования структуры плюма будем рассматривать и характерный масштаб глубины залегания нижней границы плюма h_p.

В модели поверхностного плюма при пренебрежении диффузионными процессами его толщина плавно уменьшается от значения у устья до нуля на внешней границе антициклонического вихря, который находится в циклострофическом балансе. Для этого вихря известно соотношение, позволяющее определить максимальное расстояние внешней границы поверхностного плюма от берега x_b (рис. 2) на основе только значений расхода реки, геометрии русла и плотности речных и шельфовых вод:

xb=2r=2(3g'h0+U02)f(2g'h0+ U02)1/2=Rdi2(3+Fri2)(2+ Fri2)1/2 ,                          (3)

где h₀ – глубина устья; U₀ – скорость втока реки; R_di = (g'·h₀)^1/2/f – бароклинный радиус Россби и число Фруда Fr_i для втекающего потока [9].

Согласно соотношению (3), можно рассмотреть три случая распространения плюма в зависимости от скорости втока воды из русла реки и разницы плотности речных и шельфовых вод. В случае малых скоростей втока или большой разницы плотности, когда u² << g'h₀ (что соответствует числу Фруда Fr_i << 1), из уравнения (3) следует: x_b ~ 4,2 R_di. Таким образом, внешняя граница поверхностного плюма находится на расстоянии примерно четырех бароклинных радиусов Россби от берега. Например, для Дуная это расстояние составляет x_b ~ 51 км; в области, где шельф наиболее узок, плюм достигает его границы (табл. 1, рис. 1), что согласуется с результатами наблюдений [15]. В терминах масштабов длины этот случай, для которого число Фруда Fr_i = L₀/R_di << 1, описывается как преобладание бароклинного радиуса Россби над инерционным масштабом. Скорость втока реки, глубина и ширина русла также определяют форму стокового гидрофронта и прибрежного плотностного течения через число Россби Ro = U₀/fL = L₀/L, описывающее влияние инерции и нелинейности, и число Бургера Bu = R_di/L, характеризующее влияние сил плавучести. Заметим, что число Фруда можно также выразить через их отношение как Fr_i = Ro/Bu. В данном случае влияние сил плавучести, обусловленное стоком реки, превышает влияние инерции потока. Если число Россби Ro < 1, то есть отношение инерционного масштаба к ширине русла реки меньше единицы, гидрофронт имеет полукруглую форму, прижат к берегу и формируется прибрежное течение, расход которого пропорционален экспоненте от Ro [28].

Второй предельный случай соответствует большим скоростям втока и малой разности плотности U² >> g¢h₀, что приводит к суперкритическому режиму распространения плюма c числом Фруда Fr >> 1, т. е. Ro >> Bu и ширина плюма равна удвоенному инерционному масштабу: x_b ~ 2U₀/f = 2L₀ [28]. Значение Fr ~ 1 (или Ro ~ Bu) соответствует промежуточному режиму, динамика которого сочетает черты обоих предельных случаев.

Комплексные экспедиционные исследования, направленные именно на изучение формирования и эволюции плюма Дуная, не проводились. Существующие данные в основном представлены разрозненными многолетними измерениями гидрологических, гидрооптических и гидрохимических параметров [3, 15, 29]. Из анализа гидрологических данных следует, что горизонтальный размер плюма варьирует от 28 до 120 км, толщина – от 8 до 15 м (по изохалине 16 ЕПС) [15, 29]. При размерах плюма около 90 км он занимает большую площадь шельфа, его морская граница достигает изобат 50–75 м, что влияет на гидрологическую структуру и экологическое состояние вод шельфа. На характеристики плюма значительное влияние оказывают ветровые условия. Так, аномальное южное распространение вдольберегового плотностного течения, зафиксированное в июле 1992 г., связано с продолжительным усилением северного ветра до 10 м/с в период с 12 по 18 июля [15]. С другой стороны, вытягивание плюма в северо-восточном направлении на 120 км 2–6 сентября 2004 г. обусловлено воздействием южных ветров скоростью до 10 м/с [29]. Таким образом, изменчивость стока рек и поля ветра создают разнообразные условия для формирования плюмов, что, наряду с гидрологическими условиями шельфа и отсутствием приливов, делает СЗШЧМ уникальным полигоном для изучения динамики плюмов.

Численные эксперименты с трехмерной гидродинамической моделью

В данной работе формирование и распространение плюма исследовалось методом численного моделирования с использованием трехмерной σ-координатной численной модели Princeton Ocean Model (POM), предназначенной для расчета циркуляции в прибрежной зоне с учетом стока реки [30–32]. Данные σ-координатные модели широко применяются для моделирования динамических процессов в мелководных акваториях, поскольку автоматическое сгущение σ-уровней при уменьшении глубины бассейна позволяет достичь высокого разрешения по вертикали. Кроме того, эти модели обеспечивают точное выполнение кинематических условий на свободной поверхности и на дне [31].

Расчеты выполнены для прямоугольной области. Координаты расчетной области: 29,5°–31,5° в. д., 43,35°–45,75° с. ш. Число узлов сетки по оси Х равно 51, по оси Y – 171. В начальный момент времени в модели задается поступление распресненной воды через устье реки с определенными расходом и соленостью.

Поток речных вод при отсутствии ветра и прилива распространяется в сторону моря, а затем под воздействием силы Кориолиса поворачивает в антициклоническом направлении (в Северном полушарии) [9, 31]. В результате в приустьевой зоне формируется стоковый гидрофронт и примерно через два инерционных периода устанавливается плотностное вдольбереговое струйное течение (рис. 2). В общем случае плюм представляет собой нестационарное образование, и одним из факторов, стабилизирующих его динамику, может служить стационарное фоновое течение, направленное на юг вдоль траектории распространения вдольбереговой струи распресненных вод [30–32].

Модель основана на трехмерных уравнениях циркуляции в σ-координатной системе σ = (z – η)/H, σ  [0;1], где x, y, z – декартовы координаты; H = = h+η – глубина моря; h(x, y) – рельеф дна моря; η(x, y, t) – уровень моря. Для описания динамики фронтальных зон используются примитивные уравнения движения непрерывно стратифицированной вязкой несжимаемой жидкости в приближении Буссинеска и гидростатики следующего вида:

где u, v, w – компоненты скорости по x, y, σ – соответственно; ρ₀ – средняя плотность; f – параметр Кориолиса; T, S – температура и соленость воды.

Для записи оператора переноса принято следующее обозначение:

Слагаемые HF_X, HF_Y, HF_T, HF_S параметризуют горизонтальную турбулентную вязкость и диффузию и имеют вид

A_M, A_H зависят от горизонтальных градиентов скорости:

где  и δ – некоторые константы.

Коэффициенты вертикальной турбулентной вязкости и диффузии определяются по формулам  где q²/2 – турбулентная кинетическая энергия; L – макромасштаб турбулентности; S_M, S_H – функции динамического числа Ричардсона; константы K_Mф, K_Hф – фоновые значения. Функции q, L находятся из решения уравнений баланса турбулентной энергии, решаемых совместно с основной задачей.

На поверхности и дне принимаются следующие граничные условия:

  (9)

где  – потоки тепла и соли. Выражения для касательных напряжений на свободной поверхности и на дне соответственно:  где  – плотность воздуха; ,  – коэффициенты трения; W =  – скорость ветра на высоте 10 м; U =  – горизонтальная скорость течения.

На твердых боковых границах скорости, потоки тепла и соли равны нулю.

Пространственная дискретизация уравнений выполняется на С-сетке. Используются равномерные шаги по х-, y- и σ-координате. Эволюционные уравнения интегрируются по времени с шагом Δt методом расщепления. 

Горизонтальная скорость U представляется в виде суммы независящей от глубины компоненты  – баротропной и  – бароклинной составляющих:

.

Черта над функцией обозначает результат интегрирования по σ-координате в пределах от −1 до 0. Интегрирование уравнений (4)–(6) по вертикали с использованием граничных условий (9) позволяет получить систему уравнений теории мелкой воды для определения баротропных компонент скорости и уровня моря:

Уравнения для бароклинных компонент скорости имеют следующий вид:

Задачи (10)–(12) и (13)–(14) аппроксимируются явными схемами. Причем в баротропной задаче используется малый шаг Δt_A = Δt/n, где n выбирается в соответствии с критерием устойчивости Куранта. При решении уравнений переноса тепла и соли (7)–(8) отдельно выделяется задача трехмерного переноса и горизонтальной диффузии по вертикальной координате, решаемая методом прогонки с учетом граничных условий (9).

Численный алгоритм модели основан на разделении задачи на баротропную и бароклинную моды и применении явных схем по горизонтальным координатам и неявных схем по σ-координате. Адвективный оператор в уравнениях модели аппроксимируется TVD-схемами [30], обеспечивающими монотонность численного решения, что необходимо для правильного описания полей с большими пространственными градиентами. Кроме того, недавнее исследование влияния различных численных схем на расчеты диффузии соли показало, что использование TVD-схем существенно снижает вычислительную вязкость, что приводит к меньшему искажению динамики плюма по сравнению с другими разностными схемами [33].

Прямоугольная область. В расчетах использовался прямоугольный бассейн постоянной глубины 40 м с указанными выше координатами, угол наклона дна у берега составляет от 3‧10⁻³ до 0,6‧10⁻⁴.  Начало системы координат расположено на свободной поверхности в левом нижнем углу расчетной области. Западная граница бассейна соответствует береговой черте, остальные три границы жидкие. Источник речного стока находится в узле сетки с координатами х = 2, y = 106 и характеризуется расходом воды Q_r в диапазоне от 1500 до 8000 м³/с. Замыкающий створ русла реки имеет ширину L = 1570 м и глубину h₀ = 8 м (рис. 2). В начальный момент времени соленость воды в бассейне составляла S_f = 18 ЕПС, а соленость втекающей воды варьировала от 2 до 6 ЕПС, что соответствует значениям на внутренней границе зоны смешения речных и морских вод [11]. Влияние источника наложено на фоновое меридиональное стационарное течение v₀, которое в начальный момент времени имело скорость от 5 до 25 см/c и было направлено на юг. На открытых границах расчетной области для компонент скорости течения и солености задавались условия гладкого продолжения [30], предполагающие равенство нулю нормальной производной от искомой прогностической переменной ∂φ/∂n = 0, где n – нормаль к соответствующей границе области.

Р и с.  3. Поле поверхностной солености для стока реки (Q_r = 1500 м³/с, соленость 2 ЕПС) в отсутствие ветра при значении числа Россби Ro = 0,75: а – через 1 сут; b – 5 сут (расход пресной воды в плюме через разрез CD Q_fcc = 107 м³/с); c – 10 сут (Q_fcc = 251 м³/с). Стрелками указана скорость течения; AB, CD – разрезы по широте; начальная фоновая скорость течения – 5 см/с

F i g.  3. Surface salinity field for river runoff (Q_r = 1500 m³/s, salinity is 2 PSU) in the absence of wind and at the Rossby number Ro = 0.75: a – after 1 day; b – after 5 days (freshwater transport in the plume through section CD Q_fcc = 107 m³/s); c – after 10 days (Q_fcc = 251 m³/s). Arrows indicate current velocity; AB, CD – sections by latitude; initial background current velocity is 5 cm/s

Моделирование проводилось на срок до 10–30 сут на горизонтальной сетке Δх = 3137 м, Δy = 1570 м. Для более детального разрешения по вертикальной координате использовалось 25 неравномерных уровней, сгущающихся вблизи свободной поверхности. Коэффициент горизонтальной турбулентной вязкости вычислялся по формуле Смагоринского [30]. Коэффициенты вертикальной вязкости и диффузии определялись методом Меллора – Ямады [30]. Бароклинная составляющая модели интегрировалась с шагом 2 мин, а баротропная – с шагом 6 с. Установление численного решения контролировалось по значениям кинетической энергии и расходам воды в сечениях, указанных на рис. 3.

Результаты и обсуждение

Для моделирования плюма задавались следующие параметры: ширина русла L = 1570 м, глубина русла h₀ = 8 м, расход реки Q_r в диапазоне 1500–8000 м³/с, для речных вод – соленость S в интервале 2–6 ЕПС, температура T = 15 °C, для шельфовых вод – соленость S = 18 ЕПС, T = 15 °C; плотность речных ρ₀ и морских ρ_a вод рассчитывалась из уравнения состояния для заданных значений солености и температуры; параметр Кориолиса f = 0,0001013 с⁻¹, инерционный период T0_{=2π/f=17 ч}.

Для данной конфигурации модели были выполнены расчеты, которые демонстрируют формирование и распространение плюма в отсутствие ветра и влияния стратификации вод шельфа. На рис. 3 приведено распределение солености на поверхности через 1, 5 и 10 сут для варианта 1 (табл. 2) расчета с однородной по глубине стратификацией, с расходом воды Q_r, равным 1500 м³/с, и соленостью речной воды 2 ЕПС. Число Россби Ro = 0,75 и число Бургера Bu = 6,13 характеризуют влияние сил плавучести. Число Фруда Fr_i = Ro/Bu = 0,13 (табл. 2) указывает на то, что силы плавучести, обусловленные стоком реки, преобладают над инерционными силами потока, поэтому плюм прижат к берегу. Поскольку число Россби Ro < 1, то есть отношение инерционного масштаба к ширине русла реки меньше единицы, то гидрофронт имеет полукруглую форму, прижат к берегу и вдоль побережья развивается течение (рис. 3, а).

Т а б л и ц а  2

T a b l e  2

Характеристики плюма и глубина h_p по формуле (2)

Characteristics of plume and depth h_p according to formula (2)

П р и м е ч а н и е. Модельные значения приводятся для t = 10 сут. Обозначения: X_c – смещение центра плюма от берега по широте; H_p – глубина плюма в его центре, H_cc – его глубина у берега на разрезе CD. Радиус плюма R_p, глубины H_p, H_cc определяются по положению изохалины 16 ЕПС.

N o t e. Model values are given for t = 10 days. Designations: X_c is the latitudinal displacement of plume center from the coast; H_p is the plume depth at its center; H_cc is its depth near the coast at section CD. The plume radius R_p, the depths H_p and H_cc are determined from the position of the 16 PSU isohaline.

В начальный период (через 1 сут) плюм округлой формы формируется под действием стока пресной воды от источника. Разрез AB проходит через устье по широте; а CD расположен южнее AB на ~ 31 км (рис. 3, а). Уже через 1,5–2 инерционных периода T₀ под действием силы Кориолиса от устья в антициклоническом направлении начинает формироваться вдольбереговое течение, которое затем распространяется на юг вдоль западной границы (рис. 3, b, c). Через 3,25 сут передний край фронта, который определялся по изохалине 16 ЕПС, достигает разреза СD (рис. 3). Через 5 сут формируется прибрежное плотностное течение, которое переносит часть воды из области антициклонического кругового гидрофронта на юг (рис. 3, b). При этом бόльшая часть поступающей от реки воды остается в области плюма, что приводит к росту его глубины H_p и ширины до двух радиусов 2R_p (рис. 3, с).

Через 10 сут глубина плюма H_p достигает 5 м, а радиус плюма R_p – 22,8 км, при этом рост плюма приводит к смещению его центра от берега в сторону моря на расстояние X_c, но отрыва плюма от берега не происходит, поскольку на 10-е сутки его положение стабилизируется: X_c/R_p = 0,2 (табл. 2), а его радиус достигает своего квазистационарного значения.

Увеличение расхода воды при тех же размерах устья увеличивает скорость втока реки, что приводит к росту чисел Фруда и Россби. При высокой скорости втока речной воды и узкой ширине русла (Ro_i > 1) гидрофронт принимает более округлую форму, при этом увеличивается скорость движения фронта плотностного прибрежного течения на юг. Зависимость формы гидрофронта и интенсивности прибрежного течения от числа Россби отмечается также и по данным контактных наблюдений [29]. Увеличение плотности втекаемой воды (в данных численных экспериментах через увеличение солености реки) приводит к уменьшению приведенного ускорения свободного падения g՛, что, согласно уравнению (2), увеличивает глубину плюма и число Фруда, но уменьшает роль стратификации через радиус Россби (формула (3)) и число Бургера. Величина баланса между силами плавучести и инерции определяется комбинацией расхода реки и ее плотности (солености), которые влияют на глубину плюма h_p и его радиус r, положение центра плюма и режим формирования плотностного течения. Различные варианты расчетов приведены в табл. 2. Для сравнения с плюмом, показанным на рис. 3, рассмотрим вариант 5 (табл. 2) со значением расхода реки Q_r = 8000 м³/с и соленостью S = 6 ЕПС (рис. 4). Такой режим характеризуется бόльшими значениями чисел Россби (Ro = 4), Фруда (Fr = 0,76), инерционного масштаба (L₀ = 6,3 км), но меньшими значениями числа Бургера (Bu = 5,31) и радиуса Россби (R_di = 8,3 км) (табл. 2). Хотя значение Fr = 0,76 остается ниже критического, оно почти в шесть раз превосходит значение Fr = 0,12 для варианта 1 (см. рис. 3). Таким образом, влияние инерции потока увеличилось в шесть раз по сравнению с влиянием сил плавучести. В результате плюм вытянут от берега в сторону шельфа, а его центр смещен мористее. Однако отрыва плюма от берега не происходит, так как смещение относительно его радиуса составляет X_c/R_p = 0,5 (рис. 4, с).

Поскольку в данном расчете число Россби Ro = 4 (превышает 1), то есть инерционный масштаб в четыре раза превосходит ширину русла, плюм формируется уже через 1,5 инерционных периода T₀ и имеет более круглую форму, чем на рис. 3, а. Передний край фронта вдольберегового течения достигает разреза СD через 1 сут (рис. 4). С учетом расстояния между разрезами скорость движения фронта составила С_p ~ 0,29 м/с. К 5-м суткам формируется более развитое прибрежное плотностное течение (по сравнению с рис. 3), которое переносит часть вод из области плюма через южную границу области (рис. 4, b). При этом в области плюма накапливается бόльшая часть поступающей от реки воды, что приводит к росту его глубины H_p и радиуса (рис. 4, b, с). На 10-е сутки изохалина 8 ЕПС достигает 30,5° в. д., глубина плюма H_p (определяемая по залеганию изохалины 16 ЕПС) достигает 11 м, а радиус плюма R_p – 24,4 км, при этом рост плюма сопровождается смещением его центра от берега в сторону моря на расстояние X_c. Через 10 сут его положение стабилизируется: X_c/R_p = 0,5 (табл. 2), а радиус плюма достигает устойчивого значения.

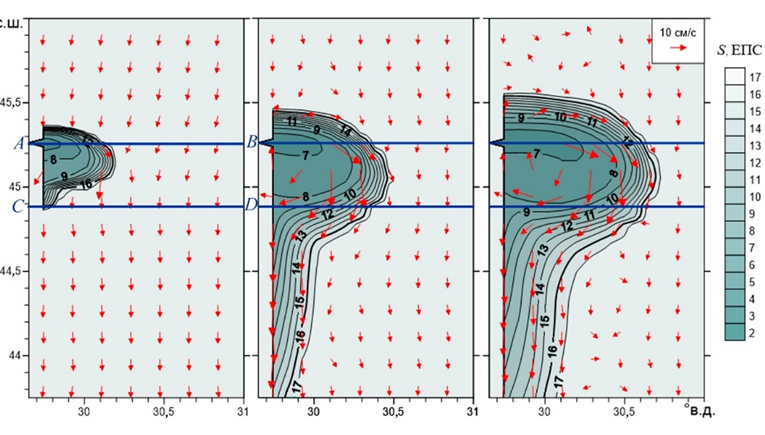
Р и с.  4. Поле поверхностной солености для стока реки в отсутствие ветра (Q_r = 8000 м³/с, соленость 6 ЕПС) при значении числа Россби Ro = 4: а – через 1 сут (Q_fcc = 25 м³/с); b – 5 сут (расход пресной воды в плюме через разрез CD Q_fcc = 1592 м³/с); c – 10 сут (Q_fcc = 1920 м³/с); Стрелками указана скорость течения; AB, CD – разрезы по широте; начальная фоновая скорость течения – 5 см/с

F i g.  4. Surface salinity field for river runoff in the absence of wind (Q_r = 8000 m³/s, salinity is 6 PSU) at the Rossby number Ro = 4: a – after 1 day (Q_fcc = 25 m³/s); b – after 5 days (freshwater transport in the plume through section CD Q_fcc = 1592 m³/s); c – after 10 days (Q_fcc = 1920 m³/s); arrows indicate current velocity; AB, CD – sections by latitude; initial background current velocity is 5 cm/s

Представление о вертикальной структуре плюма дают разрезы солености AB на рис. 5. Соленость S реки в обоих случаях одинакова – 6 ЕПС, различается только расход Q_r: 3000 м³/с (рис. 5, а, b, c) и 8000 м³/с (рис. 5, d, e, f).

Увеличение расхода реки для случая, когда S = 2 ЕПС, Q = 3000 м³/с, в два раза приводит к росту скорости втока и, как следствие, к увеличению чисел Россби (Ro = 4) и Фруда (Fr = 0,76). Это обусловливает формирование плюма, более вытянутого в сторону шельфа, а инерционный радиус возрастает до 6,3 км (рис. 5, d, e, f) по сравнению с 2,4 км в первом случае (рис. 5, а, b, c). Поскольку число Фруда во втором случае в 2,7 раза больше и приближается к критическому значению, точка отрыва плюма от дна смещается в сторону шельфа (см. рис. 2), а накопление бόльшей части поступающей от реки воды приводит к росту глубины плюма до 11 м против 6,3 м в первом случае (рис. 5, c, f). После формирования плюма и прибрежного течения через 1,5–3 инерционных периода скорости находятся в геострофическом балансе с градиентом давления.

Р и с.  5. Зональные разрезы AB (см. рис. 4) поля солености через 1, 5 и 10 сут (S = 6 ЕПС) при расходе Q_r, равном 3000 м³/с (а, b, c), 8000 м³/с (d, e, f). Красным цветом выделена изохалина 16 ЕПС

F i g.  5. Zonal sections AB (see Fig. 4) of salinity field after 1, 5 and 10 days (S = 6 PSU) at a discharge Q_r equal to 3000 m³/s (a, b, c), 8000 m³/s (d, e, f). The 16 PSU isohaline is highlighted in red

Р и с.  6. Радиус плюма, полученный по модельным данным R_p(t) при S = 2 ЕПС и Q_r, равном 1500 м³/с (1), 3000 м³/с (2); 8000 м³/с (3); при S = 6 ЕПС и Q_r, равном 3000 м³/с (4); 8000 м³/с (5); радиус r(t) (6), рассчитанный по формуле (15) при S = 2 ЕПС, Q_r = 3000 м³/с, ω = −0,8f и h_max = 6,5 м (табл. 2)

F i g.  6. Plume radius obtained from the model data R_p(t) at S = 2 PSU and Q_r equal to 1500 m³/s (1), 3000 m³/s (2); 8000 m³/s (3); at S = 6 PSU and Q_r equal to 3000 m³/s (4); 8000 m³/s (5); radius r(t) (6) calculated by formula (15) at S = 2 PSU, Q_r = 3000 m³/s, ω = −0.8f and h_max = 6.5 m (Table 2)

Кроме того, движение вод внутри ядра плюма можно рассматривать как вращение твердого тела, поскольку наблюдения и лабораторные эксперименты показывают, что завихренность в ядре плюма постоянна и близка по величине к параметру Кориолиса. В рамках этого предположения в работе [13] получено соотношение для максимальной кривизны и глубины плюма, позволяющее оценить его радиус в зависимости от завихренности:

r=(-4g' ∙hmaxω∙ω2+f )12 ,                                            (15)

где r – радиус плюма; h_max – его максимальная глубина; ω – средняя завихренность; f – параметр Кориолиса; g'  – приведенное ускорение свободного падения. По результатам моделирования радиус и глубина залегания плюма оценивались по положению изохалины 16 ЕПС.

Эволюция радиуса плюма относительно его центра X_c для разных экспериментов приводится на рис. 6 (табл. 2). Средняя завихренность плюма ω составляла от −0,95f до −0,6 f. Во всех экспериментах центр плюма удаляется от берега с увеличением числа Фруда, однако отрыва плюма от берега не происходит: отношение X_c к радиусу плюма увеличивается от 0,2 при расходе 1500 м³/с и Fr = 0,13 до 0,5–0,6 при Fr = 0,76, везде оставаясь меньше 1 (табл. 2). В течение 1,5–3 инерционных периодов наблюдается резкий рост радиуса плюма (рис. 6). После формирования прибрежного течения и установления геострофического баланса радиус увеличивается линейно со временем и достигает 21–24 км (рис. 6). Графики R_p(t), полученные из модельных данных, хорошо аппроксимируются зависимостью (15) при ω = −0,8f и максимальной глубине плюма h_max(t), определенной по изохалине 16 ЕПС. Следует отметить, что оценка радиуса плюма по формуле (3) занижает значения r для всех вариантов из табл. 2, так как соответствует стационарному случаю. Для всеx графиков на рис. 6 число Fr < 1, а отношение радиуса плюма к бароклинному радиусу R_di составляет 2,2–2,9, что соответствует классификации плюмов на основе уравнения (3) для случая малых скоростей втока и большой разницы плотностей u² << g'h₀ с числом Фруда Fr_i < 1 и оценкой r ~ 2,1R_di.

После установления геострофического режима циркуляции в плюме и продвижения фронта прибрежного течения на юг перенос этим течением пресной воды Q_fcc через вертикальный разрез CD оценивался по формуле

Qfcc(t)=CDS0  -St,x,zS0Vt,x,zdxdz,                        (16)

где S₀ = 18 ЕПС – соленость вод шельфа; V – меридиональная компонента скорости; интегрирование производится по разрезу CD (см. рис. 3, 4).

Рост расхода воды при тех же размерах устья увеличивает скорость втока реки, что приводит к росту чисел Фруда и Россби. При высокой скорости втока речной воды и узкой ширине русла (Ro_i > 1) гидрофронт принимает более округлую форму, при этом увеличивается скорость движения фронта плотностного прибрежного течения на юг. Зависимость формы гидрофронта и интенсивности прибрежного течения от числа Россби отмечается также и по данным контактных наблюдений [13].

Учитывая, что количество пресной воды, поступающей в плюм, зависит от солености речной воды в русле, введем нормированную величину расхода пресной воды прибрежным течением: Q^*_fcc = Q_fcc/(γQ_r), где γ = (S₀ – S)/S₀ – доля пресной воды в реке. Графики Q^*_fcc для различных вариантов моделирования приведены на рис. 7. При одинаковых расходах реки транспорт пресной воды прибрежным течением тем больше, чем меньше соленость реки S (рис. 7), т. е. он пропорционален увеличению доли пресной воды в реке γ в соответствии с формулой (16). При одинаковой солености (т. е. фиксированном значении γ) с увеличением расходов реки и, соответственно, увеличением скоростей втока воды в устье возрастают скорости в плюме и прибрежном течении. Согласно формуле (16), это приводит к росту Q^*_fcc пропорционально величине Q_r реки (рис. 7).

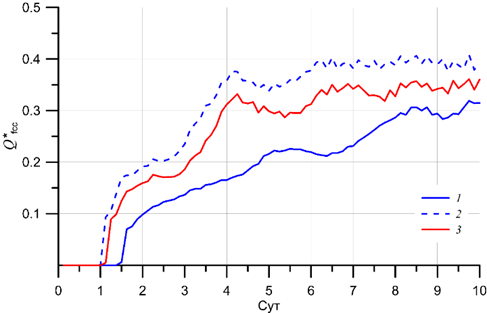
Р и с.  7. Расход пресной воды Q^*_fcc через разрез CD, по модельным данным, нормированный на пресноводный расход реки Q_fw = (S_a – S₀)/(S_a·Q_r), при S = 2 ЕПС и Q_r, равном 3000 м³/с (1), 8000 м³/с (2); при S = 6 ЕПС и Q = 8000 м³/с (3)

F i g.  7. Freshwater discharge Q^*_fcc through section CD based on model data, normalized to the river freshwater discharge Q_fw = (S_a – S₀)/(S_a·Q_r), with S = 2 PSU and Q_r equal to 3000 m³/s (1), 8000 m³/s (2); with S = 6 PSU and Q = 8000 m³/s (3)

Заметим, что через 4–5 сут зависимость расходов от времени для всех вариантов становится близкой к линейной (рис. 7). Это связано с тем, что за указанное время передний край фронта вдольберегового течения достигает южной границы расчетной области и устанавливается квазистационарный режим плюма (см. рис. 3, 4). Потенциальная энергия прибрежного течения E_p = (g՛·h), рассчитанная по модельным данным, где h – глубина течения у берега, показывает аналогичную Q^*_fcc временну́ю зависимость. В работе [28] для случая равенства температур вод шельфа и реки и линейной зависимости уравнения состояния от солености (Δρ = β·ΔS) показано, что величину Q_fcc по формуле (16) можно оценить как Q_fcc≈ С·E_p²/f, где С = ρ₀/(2·g·β·S₀) – константа. Таким образом, расход пресных вод зависит только от квадрата потенциальной энергии прибрежного течения.

По мере развития плюма и достижения передним фронтом прибрежного течения разреза CD начинается рост расхода Q^*_fc в течение 4–5 сут (см. рис. 4), который к 10-м суткам переходит в квазистационарный режим. В этом случае расход прибрежного течения описывается соотношением Qfcc*=1/(1+2·α), где α = −2·U_θ/f·r – средняя завихренность ядра плюма, нормированная на параметр Кориолиса [13], U_θ = −(18·Q_r·f·g՛)^1/4 – азимутальная скорость плюма [33]; r – радиус плюма. Величина Q^*_fcc оценивалась по приведенным формулам с использованием радиуса плюма и g՛ из модельных данных для момента времени t = 10 сут (табл. 2), когда расходы Q^*_fcc были близки к стационарным (см. рис. 6). Для второго варианта расчетов (α = 0,83, Q^*_fcc = 0,38); третьего (α = 0,93, Q^*_fcc = = 0,35); пятого (α = 0,87, Q^*_fcc = 0,37) отмечается совпадение с модельными значениями Q^*_fcc (см. рис. 6). Таким образом, для расходов реки от 3000 до 8000 м³/с и солености втекающей воды от 2 до 6 ЕПС при выходе расхода пресных вод на квазистационарный режим около 40 % речных вод переносится прибрежным течением, а около 60 % остается циркулировать в плюме, что приводит к его увеличению и медленному росту глубины и радиуса (см. рис. 6). Такое распределение стока реки наблюдалось как в лабораторных экспериментах и при численном моделировании [10, 13], так и при анализе гидрологических данных в районах образования плюма [13].

Фоновое течение, совпадающее по направлению с распространением прибрежного плотностного течения от устья реки, стабилизирует плюм и ускоряет движение фронта. При повторении расчетов с фоновым течением скоростью от 10 до 25 см/с наблюдался рост Q^*_fcc и более быстрый выход на квазистационарный режим. Например, при скорости фонового течения V_fon = 25 см/с значение Q^*_fcc увеличивалось в два раза по сравнению с вариантом при V_fon = 5 см/с на 5-е сутки расчета. Полученные результаты справедливы не только при отсутствии ветрового воздействия, но и при слабых ветрах. В работе [20] было показано, что при формировании плюма ветровое воздействие начинает преобладать над плавучестью, обусловленной поступлением пресных речных вод, при силе ветра более 5,7 м/с для средней величины стока Дуная 6000 м³/с и типичных для СЗШЧМ значений плотности морской воды (приведенное ускорение свободного падения g՛ ~ 0,02÷0,11 м/с²). Таким образом, для слабых ветров (со скоростью менее 5 м/с) формулы (1), (15) позволяют оценивать характерную глубину и горизонтальный масштаб плюма, что можно использовать при анализе контактных и спутниковых данных.

Заключение

На основе численного моделирования с использованием трехмерной σ-координатной численной модели POM были проведены расчеты циркуляции в прибрежной зоне с учетом стока реки. Исследовалось формирование речного плюма и прибрежного плотностного течения при различных расходах реки и стратификации вод шельфа, характерных для СЗШЧМ.

Адвективный оператор в уравнениях модели аппроксимировался TVD-схе-мами, что обеспечило монотонность численного решения в областях с большими пространственными градиентами гидрофизических параметров. Использование TVD-схем позволило также существенно снизить вычислительную вязкость, что привело к меньшему искажению динамики плюма по сравнению с другими разностными схемами. 

Формирование и эволюция плюма моделировались для пяти вариантов с разными значениями солености и расхода реки в диапазоне чисел Фруда от 0 до 1. В этих случаях силы плавучести, обусловленные стоком реки, преобладают над инерцией потока, поэтому плюм остается прижатым к берегу. Плюм имеет полукруглую форму. Если при этом число Россби Ro < 1, то есть отношение инерционного масштаба к ширине русла реки меньше единицы, плюм остается прижатым к берегу. Баланс между силами плавучести (число Бургера) и инерции (число Фруда и Россби) зависит от комбинации расхода реки и ее плотности (солености), которые влияют на глубину плюма, его радиус, форму, положение центра и на режим формирования плотностного течения.

На начальном этапе (время t ~ T₀, где T₀ – инерционный период) у русла реки начинает развиваться антициклонический вихрь. К моменту t ~ 2T₀ вихрь формирует ядро плюма и, достигая берега южнее русла, формирует плотностное прибрежное течение, которое переносит пресные воды на юг. После t ~ 2T₀ циркуляция воды в плюме и течении подчиняется геострофическому балансу с кросс-шельфовым градиентом давления.

Плюм состоит из области ядра, в котором азимутальная скорость растет линейно от его центра, и внешней области, в которой скорости близки к нулю. Такая структура плюма подтверждается лабораторными экспериментами и наблюдениями и свидетельствует о постоянстве завихренности ω в ядре плюма, при этом значение ω ~ −f, то есть потенциальная завихренность близка к нулю. Внешняя морская граница плюма и его глубина совпадают с положением изохалины 16 ЕПС, а радиус плюма R_p, рассчитанный c учетом максимальной глубины плюма и средней завихренности плюма ω (формула (15)) лучше соответствует модельным значениям R_p, чем стационарная оценка (формула (3)). При увеличении отношения инерционного масштаба к радиусу Россби радиус плюма также увеличивается и достигает R_p = 24 км для эксперимента с Fr = 0,76, при этом отношение R_p к радиусу Россби достигает 2,9, а центр плюма смещается в сторону моря на расcтояние 0,5 R_p. Рассчитанные по модели глубина плюма H_p и скорость прибрежного течения превышают оценки (1) в 2,4–3,1 раза, однако значения H_p и ширины плюма x_b = 2R_p согласуются с данными гидрологических наблюдений, выполненных в условиях слабого ветра (~ 5 м/с).

Скорость движения переднего края фронта плотностного прибрежного течения, согласно модельным оценкам, соответствует скорости движения гравитационного течения вдоль склона шельфа С_p и составляет ~ 0,15–0,32 м/с. Расход пресной воды Q^*_fcc, переносимой течением, пропорционален квадрату его потенциальной энергии. После t ~ 5T₀ зависимость Q^*_fcc от квадрата потенциальной энергии описывается линейной регрессией с коэффициентом детерминации ~ 0,95 и корреляции ~ 0,97. Спустя 10 дней (t ~ 10T₀) устанавливается квазистационарный режим, при котором расход прибрежного течения составляет около 40 % от общего стока реки, при этом 60 % продолжают циркулировать в плюме, что приводит к его дальнейшему росту.

Полученные соотношения для глубины и ширины плюма, расхода прибрежного течения можно использовать для оценки этих параметров по гидрологической информации или спутниковым данным при скорости ветра менее 5 м/с. Результаты статьи могут использоваться для планирования морских экспедиций в прибрежной зоне с речным стоком, оценки влияния катастрофических сбросов воды или паводков в реках на гидрохимический режим и экологическое состояние прибрежной зоны. Результаты могут использоваться для развития методов анализа спутниковых данных, поскольку установленные в работе регрессионные соотношения позволяют оценивать изменчивость расхода пресных вод в прибрежной зоне Q^*_fcc по спутниковым измерениям.

1. Zav'yalov P., Makkaveev P. Rechnye plyumy v akvatorii Sochi // Nauka v Rossii. 2014. № 2. S. 4–12. EDN STAQAB.

2. Osadchiev A., Sedakov R., Barymova A. Response of a small river plume on wind forcing // Frontiers in Marine Science. 2021. Vol. 8. 809566. https://doi.org/10.3389/fmars.2021.809566

3. Kondrat'ev S. I. Tri harakternye gidrologo-gidrohimicheskie situacii vozle ust'ya Dunaya po dannym ekspedicionnyh issledovaniy Morskogo gidrofizicheskogo instituta v 1997–2013 godah // Morskoy gidrofizicheskiy zhurnal. 2019. T. 35, № 4. S. 367–383. EDN BTJNWV. https://doi.org/10.22449/0233-7584-2019-4-367-383

4. Osadchiev A. A. Rechnye plyumy. Moskva : Nauchnyy mir, 2021. 286 s.

5. O perenose stoka malyh rek vdol'beregovym baroklinnym morskim techeniem / V. M. Zhurbass [i dr.] // Okeanologiya. 2011. T. 51, № 3. S. 440–449. EDN NWCMRX.

6. Whitehead J. A. The deflection of a baroclinic jet by a wall in a rotating fluid // Journal of Fluid Mechanics. 1985. Vol. 157. P. 79–93. https://doi.org/10.1017/S0022112085002312

7. Garvine R. W. Estuary plumes and fronts in shelf waters: a layer model // Journal of Physical Oceanography. 1987. Vol. 17, iss. 11. P. 1877–1896. https://doi.org/10.1175/1520-0485(1987)017<1877:EPAFIS>2.0.CO;2

8. Garvine R. W. A dynamical system for classifying buoyant coastal discharges // Continental Shelf Research. 1995. Vol. 15, iss. 13. P. 1585–1596. https://doi.org/10.1016/0278-4343(94)00065-U

9. Yankovsky A. E., Chapman D. C. A simple theory for the fate of buoyant coastal discharges // Journal of Physical Oceanography. 1997. Vol. 27, iss. 7. P. 1386–1401. https://doi.org/10.1175/1520-0485(1997)027<1386:ASTFTF>2.0.CO;2

10. Horner-Devine A. R., Hetland R. D., MacDonald D. G. Mixing and transport in coastal river plumes // Annual Review of Fluid Mechanics. 2015. Vol. 47. P. 569–594. https://doi.org/10.1146/annurev-fluid-010313-141408

11. Mihaylov V. N., Mihaylova M. V., Frolova N. L. Smeshenie rechnyh i morskih vod na ust'evom vzmor'e krupnoy reki // Vestnik Moskovskogo universiteta. Seriya 5: Geogra-fiya. 1985. № 6. S. 37–42. EDN UDCWCF.

12. Garvine R. W. Physical features if the Connecticut River outflow during high discharge // Jour-nal of Geophysical Research. 1974. Vol. 79, iss. 6. P. 831–846. https://doi.org/10.1029/JC079i006p00831

13. Horner-Devine A. R. The bulge circulation in the Columbia River plume // Continental Shelf Research. 2009. Vol. 29, iss. 1. P. 234–251. https://doi.org/10.1016/j.csr.2007.12.012

14. Kourafalou, V. H., Stanev E. V. Modeling the impact of atmospheric and terrestrial inputs on the western Black Sea coastal dynamics // Annales Geophysicae. 2001. Vol. 19, iss. 2. P. 245–256. https://doi.org/10.5194/angeo-19-245-2001

15. Yankovsky A., Lemeshko E., Ilyin Y. The influence of shelfbreak forcing on the alongshelf pene-tration of the Danube buoyant water, Black sea // Continental Shelf Research. 2004. Vol. 24, iss. 10. P. 1083–1098. https://doi.org/10.1016/j.csr.2004.03.007

16. Avicola G., Huq P. Scaling analysis for the interaction between a buoyant coastal current and the continental shelf: experiments and observations // Journal of Physical Oceanography. 2002. Vol. 32, iss. 11. P. 3233–3248. https://doi.org/10.1175/1520-0485(2002)032<3233:SAFTIB>2.0.CO;2

17. Pathways and mixing of the north western river waters in the Black Sea / S. Miladinova [et al.] // Estuarine, Coastal and Shelf Science. 2020. Vol. 236. 106630. https://doi.org/10.1016/j.ecss.2020.106630

18. Modelirovanie raspresnyayuschego effekta rechnogo stoka vo vremya vesennego polovod'ya na severo-zapadnom shel'fe Chernogo morya / V. A. Ivanov [i dr.] // Izvestiya RAN. Fizi-ka atmosfery i okeana. 1996. T. 32, № 1. S. 152–160.

19. Romanian coastal dynamics during cold and warm seasons analyzed by means of a numerical model / I. Dinu [et al.] // Geo-Eco-Marina. 2017. Vol. 23. P. 71–102. https://doi.org/10.5281/zenodo.1194142

20. Tsyganova M. V., Lemeshko E. M. Interannual variability of the wind field on the Black Sea north western shelf and its impact on river plume formation for decade 2011–2020 // Proceed-ings of SPIE. Tomsk : SPIE, 2021. Vol. 11916 : 27th International Symposium on Atmospher-ic and Ocean Optics, Atmospheric Physics. 119163G. https://doi.org/10.1117/12.2603268

21. Gidrometeorologiya i gidrohimiya morey SSSR. T. 4. Chernoe more. Vyp. 1. Gidrometeo-rologicheskie usloviya / Pod red. A. I. Simonova i E. I. Al'tmana. Leningrad : Gidro-meteoizdat, 1991. 430 s.

22. Kosarev A. N., Arhipkin V. S., Katysheva M. V. Gidrologicheskaya struktura vod severo-zapadnoy chasti Chernogo morya // Vestnik Moskovskogo universiteta. Seriya 5: Geografiya. 2001. № 5. S. 50–54.

23. Dzhaoshvili Sh. Reki Chernogo morya. Tbilisi : Evropeyskoe agentstvo po ohrane okru-zhayuschey sredy, 2002. 58 s. (Tehnicheskiy otchet № 71).

24. Tsyganova M. V., Zavialov P. O., Lemeshko E. M. The interannual variability of suspended matter concentration in the North-Western part of the Black Sea // Proceedings of SPIE. Tomsk : SPIE, 2018. Vol. 10833 : 24th International Symposium on Atmospheric and Ocean Optics: Atmospheric Physics. 1083328. https://doi.org/10.1117/12.2504485

25. Comparative analysis of the first baroclinic Rossby radius in the Baltic, Black, Okhotsk, and Mediterranean seas / A. Kurkin [et al.] // Russian Journal of Earth Sciences. 2020. Vol. 20. ES4008. https://doi.org/10.2205/2020ES000737

26. The Columbia River plume study: Subtidal variability in the velocity and salinity fields / B. M. Hickey [et al.] // Journal of Geophysical Research: Oceans. 1998. Vol. 103, iss. C5. P. 10339–10368. https://doi.org/10.1029/97JC03290

27. An observational study of the Mississippi-Atchafalaya Coastal Plume. Final Report / S. P. Murray, ed. New Orleans, LA : US Department of the Interior, 1998. 544 p. (OCS Study MMS 98-0040).

28. Fong D. A., Geyer W. R. The alongshore transport of freshwater in a surface-trapped river plume // Journal of Physical Oceanography. 2002. Vol. 32, iss. 3. P. 957–972. https://doi.org/10.1175/1520-0485(2002)032<0957:TATOFI>2.0.CO;2

29. River-induced particle distribution in the northwestern Black Sea (September 2002 and 2004) / A. P. Karageorgis [et al.] // Journal of Geophysical Research: Oceans. 2009. Vol. 114, iss. C12. C12003. https://doi.org/10.1029/2009JC005460

30. Fomin V. V., Polozok A. A. Osobennosti formirovaniya rechnogo plyuma v melkovodnoy lagune (na primere zaliva Sivash, Azovskoe more) // Ekologicheskaya bezopasnost' pri-brezhnoy i shel'fovoy zon morya. 2022. № 3. S. 28–42. https://doi.org/10.22449/2413-5577-2022-3-28-42

31. Ivanov V. A., Fomin V. V. Matematicheskoe modelirovanie dinamicheskih processov v zone more – susha. Sevastopol' : EKOSI-Gidrofizika, 2008. 363 s.

32. Cyganova M. V., Lemeshko E. M., Ryabcev Yu. N. Vliyanie apvellinga na razvitie rechnogo plyuma v pribrezhnoy zone severo-zapadnogo shel'fa Chernogo morya na osnove chislennogo modelirovaniya // Ekologicheskaya bezopasnost' pribrezhnoy i shel'fovoy zon morya. 2023. № 1. S. 20–30. EDN SYKFPE. https://doi.org/10.22449/2413-5577-2023-1-20-30

33. Plume spreading test case for coastal ocean models / V. Fofonova [et al.] // Geoscientific Model Development. 2021. Vol. 14, iss. 11. P. 6945–6975. https://doi.org/10.5194/gmd-14-6945-2021