Arakawa–Lamb scheme for discrete equations of the horizontal components of three-dimensional absolute vorticity of an ideal fluid, and also at analyzing their features. Methods and Results. To derive the finite-difference three-dimensional equations of absolute vorticity, the grid containing more unknowns than equations is applied, that permits to obtain the discrete equations of motion which, in their turn, yield the equation for absolute vorticity. The resulting expression is presented in a form of three terms reflecting different features of the discrete equations. The first term provides the fulfillment of an energy conservation law for discrete statement, the second term – the presence of two quadratic invariants for the case of a divergence-free flow, the addition of the third term results in the Arakawa–Lamb scheme at the shallow water approximation. It follows from the presented expression that the second and third terms, for which there are no analogues in the continuous statement, can be interpreted as a zero approximation with the second order of accuracy. Thus, selection of these expressions makes it possible to construct the schemes with the required features of conservation laws. Conclusions. The presented form of discrete equation of the three-dimensional absolute vorticity allows constructing the schemes with the previously set features. The difference equations for the horizontal components of absolute vorticity are derived, they possess two quadratic invariants.
Arakawa-Lamb scheme, discrete equations of model, sea dynamics, kinetic energy, absolute vortex, quadratic invariants
Введение
Одним из фундаментальных результатов в исследовании дифференциальных уравнений в частных производных остается теорема Нетер [1], которая устанавливает взаимно однозначное соответствие между свойствами решения таких систем и законами сохранения, которыми они обладают. Явным примером ее приложения для уравнений мелкой воды является схема сохранения энергии и потенциальной энстрофии (законы сохранения), что обеспечивает постоянство среднего волнового числа, взвешенного по энергии (свойство решения).
Для разностной системы уравнений двумерной динамики в работе [2] были получены схемы, сохраняющие энергию и квадрат вихря для бездивергентного движения. Для приближения мелкой воды в [3] приведена дискретная система уравнений, которая обладает двумя квадратичными инвариантами – энергией и потенциальной энстрофией. Как следствие этого свойства, в соответствии с дифференциальной постановкой запрещается передача энергии в сторону одних масштабов, например в малые. В работе [4] получена дискретизация скобки Намбу с сохранением свойства антисимметрии, что позволило обобщить схему Аракавы – Лэмба и получить разностную схему, полностью (по времени и пространству) обладающую двумя дискретными квадратичными инвариантами (энергия и потенциальная энстрофия). На ее основе выводятся явные конечно-разностные уравнения мелкой воды, которые сохраняют массу, циркуляцию, энергию и потенциальную энстрофию на регулярной квадратной сетке и на неструктурированной треугольной сетке. Последняя включает в себя регулярную шестиугольную сетку как частный случай.
В работе [5] классическая схема Аракавы – Лэмба, выписанная для ортогональных квадратных сеток, представлена на произвольных неортогональных полигональных сетках и схема, полученная в работе [4], обобщена на произвольные ортогональные сферические полигональные сетки таким образом, чтобы обеспечить сохранение энергии и потенциальной энстрофии. Для уравнений мелкой воды в случае обобщенных криволинейных координат в работе [6] на основе тензорного анализа выводится конечно-разностная схема, сохраняющая энергию и потенциальную энстрофию. Показано, что точное сохранение дискретной энергии и потенциальной энстрофии предотвращает искажение прямого и обратного каскадов энергии в квазидвумерной турбулентной жидкости и повышает устойчивость схемы.
Для уравнений мелкой воды, которые включают полную силу Кориолиса и рельеф дна, в работе [7] выведена схема, сохраняющая энергию и потенциальную энстрофию. Авторы отмечают, что сохранение дискретной энергии и дискретной потенциальной энстрофии предотвращает искажение прямого и обратного каскадов энергии в квазидвумерной турбулентности и повышает устойчивость схемы.
В настоящей работе, которая является продолжением исследований [8, 9], схема Аракавы – Лэмба переписывается специальным образом. Полученная запись позволяет, во-первых, выделить явным образом слагаемые, ответственные за разные свойства сохранения в уравнении для абсолютного вихря скорости, и, во-вторых, обобщить схему для дискретных уравнений горизонтальных компонент вихря скорости.
Дискретные уравнения движения
Рассмотрим дифференциальные уравнения несжимаемой жидкости в поле потенциальных сил при отсутствии вязкости и внешних источников. Тогда в приближении Буссинеска в декартовой системе координат скорость движения в области W с границей ¶W в форме Громеки – Лэмба удовлетворяет следующей системе уравнений:
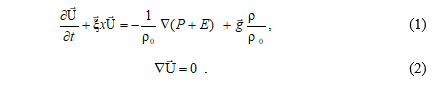
Введены обозначения: 
– компоненты вектора скорости течения по осям (x, y, z), направленным на восток, север и вертикально вниз соответственно; 
= (0, 0, g) – ускорение свободного падения ; (P, r) – давление и плотность морской воды; r0 = 1 г/см3 (в дальнейшем полагаем давление и плотность нормированными на r0); 
= 
– параметр Кориолиса, где 
= 2w sinj; w – угловая скорость вращения Земли; j – широта.
В уравнении (1) введены абсолютный вихрь скорости и кинетическая энергия движения:
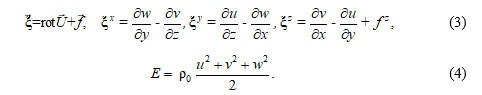
В терминах тензорного анализа
где 
Здесь и далее 
одновременно могут принимать только разные значения 
; 
– тензор Леви-Чивиты и для каждого фиксированного α суммирование осуществляется по β, γ.
При z = 0 
при z = H(x, y) 
. (5)
На боковых стенках ставятся условия непротекания:
для меридиональных 
для зональных участков границы 
(6)
Начальные условия:
при t = t0 u = u0, v = v0, w = w0.
Уравнение для абсолютного вихря скорости имеет вид
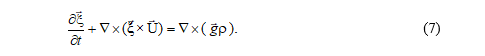
Аппроксимируем бассейн с неровным дном боксами, центрам которых соответствуют целочисленные значения индексов i, j, k (
k = 1,…, Ki,j), граням – i+1/2, j+1/2, k+1/2. Горизонтальные размеры боксов (
) постоянные, по вертикали используется неравномерная аппроксимация (
).
Разностные операторы имеют вид (для j, k – аналогично):
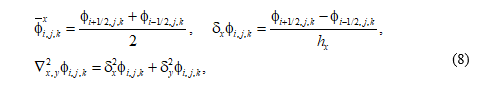
На горизонтах 
рассчитываются горизонтальные компоненты скорости, на горизонтах 
– вертикальная скорость; 
– площадь поверхности на горизонте k. Распределение переменных указано на рисунке.
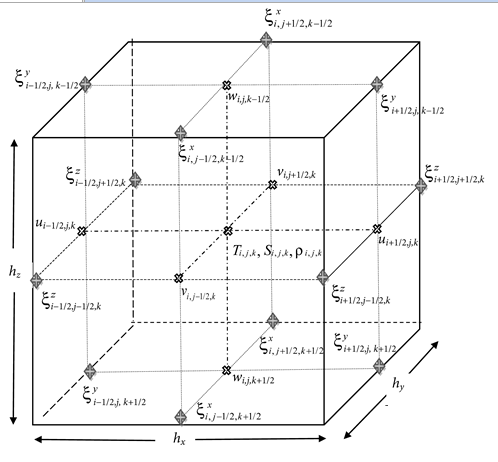
Распределение переменных в боксе (i, j, k), на его ребрах – компоненты абсолютного вихря скорости 
Distributions of variables in the box (i, j, k) and on its edges are the absolute vorticity components 
Выпишем дифференциально-разностные уравнения движения (дифференциальные по времени) [3, 9]:
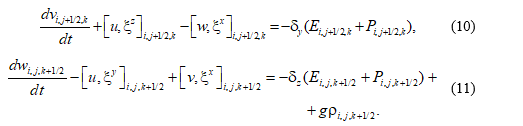
Для дискретных аналогов нелинейных слагаемых введены обозначения
, конкретный вид которых представим позже.
В соответствии с обозначениями (3), (4), (8) компоненты вихря скорости (рисунок) и кинетическая энергия имеют вид
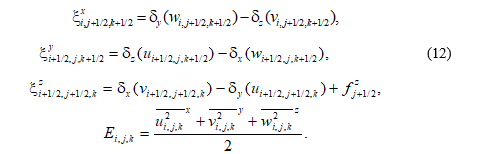
Из аппроксимации (5) следует, что в точках 
выполняется
Рассмотрим движение в плоскости (x, y). В отличие от классической работы [3], запишем нелинейное слагаемое в первом уравнении и – во втором в следующем виде:
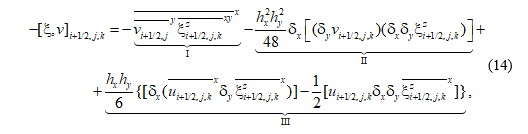
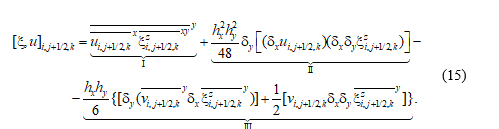
Переходя к дискретным уравнениям бездивергентного течения в плоскости (x, y), после известных преобразований с учетом равенства (13) получим уравнение для вихря скорости. Дифференциальное уравнение вихря обладает законами сохранения энергии, вихря и энстрофии (квадрат вихря), которые должны соблюдаться в разностной задаче. Смысл записи нелинейных слагаемых в уравнениях (9), (10) в виде выражений (14), (15) заключается в следующем. Разностное слагаемое, обозначенное цифрой I, соответствует дифференциальному аналогу горизонтальной адвекции. В разностном уравнении для вихря скорости оно обеспечивает выполнение закона сохранения дискретной энергии, но вихрь и энстрофия не являются инвариантами. Член, обозначенный цифрой II, имеет четвертый порядок малости и поэтому порядок разностной схемы не меняет. Но его присутствие в выражениях (14), (15) обеспечивает в дискретном уравнении для вихря скорости бездивергентного течения выполнение законов сохранения вихря, энергии и энстрофии [2].
Третье слагаемое второго порядка малости принципиально отличается от двух других. Если первые два могут интерпретироваться как приближение 
, то третий член формально никакому слагаемому не соответствует. Он появляется в результате требования консервативности дискретного уравнения вихря, обеспечивая наряду с первым слагаемым сохранение энергии и потенциальной энстрофии в модели мелкой воды (дивергентное движение в плоскости (x, y)) [3].
Из представленных рассуждений следует, что уравнения движения в приближении мелкой воды могут быть записаны в следующем виде:
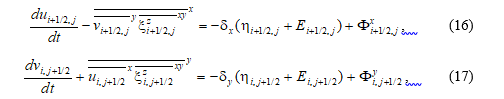
где 
– возвышение свободной поверхности. В уравнениях (16), (17) вид 
очевиден.
Из сказанного следует два вывода. Во-первых, методом построения разностных схем, обладающих нужными свойствами сохранения, может служить выбор подходящих выражений типа
, которые порядок задачи не меняют и могут интерпретироваться как приближение нуля с соответствующим порядком. Во-вторых, уравнения (16), (17) могут быть записаны в терминах тензорного анализа:
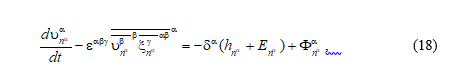
где a, b, g одновременно могут принимать только разные значения x, y, z.
Выражения для 
приведем позже.
Введены следующие обозначения: 
,
где 
соответствуют точкам (i+1/2, j, k), (i, j+1/2, k), (i, j, k+1/2).
Если в уравнении (18) примем a = x, то получим уравнение (16), если a = y, то получим уравнение (17). Иначе говоря, переставляя местами a и b, мы получаем систему (16), (17).
С учетом введенных обозначений запишем уравнения (9)–(11) в виде одного:
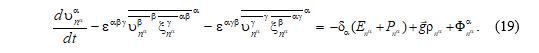
Пусть в уравнении (19) 
, тогда получаем
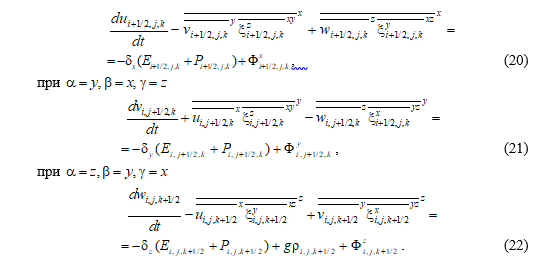
Рассмотрим последнее слагаемое в уравнении (19). Представим его в виде
. 
Тогда в соответствии с выражениями (14), (15) слагаемые в равенстве (23) можем записать следующим образом
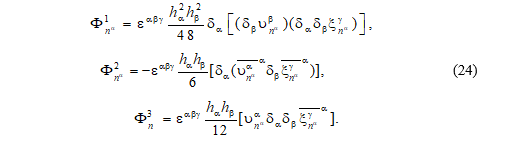
Заметим, что здесь и далее суммирование осуществляется при фиксированном a по двум перестановкам – b, g и g, b. Поэтому уравнения (21)–(22) с учетом выражения (24) могут быть записаны в виде одного уравнения
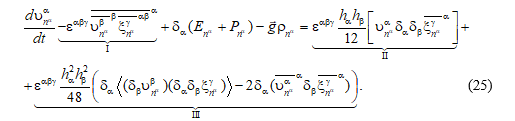
Дискретное уравнение (25) обладает следующими особенностями. Слагаемое I является дискретным аналогом нелинейного члена в уравнении движения. В случае приближения мелкой воды выполняется закон сохранения энергии, но нет гарантии сохранения потенциальной энстрофии (второй квадратичный инвариант). Добавление члена, отмеченного как II, приводит к схеме, обеспечивающей наличие двух дискретных инвариантов – энергии и энстрофии (квадрат вихря) для бездивергентного течения, но по-прежнему для приближения мелкой воды отсутствует свойство сохранения потенциальной энстрофии. И, наконец, слагаемое III приводит к схеме Аракавы – Лэмба [3].
Правая часть формально не соответствует дифференциальному виду уравнения (1), но порядок схемы не меняет и может интерпретироваться как аппроксимация нуля со вторым порядком точности по пространственным координатам.
В указанных обозначениях абсолютный вихрь скорости (12) переписывается в виде (разностный аналог (3))
Проведя соответствующие операции, получаем дифференциально-разностное (дифференциальное по времени) уравнение для абсолютного вихря скорости (дискретный аналог уравнения (7)):
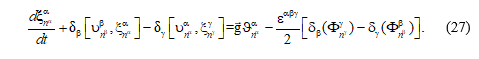
Квазистатическое приближение
Рассмотрим частный случай движения в квазистатическом приближении с учетом краевых (6) и начальных условий. В этом случае
Уравнение неразрывности имеет прежний вид (2).
Напомним, что предполагаем
В соответствии с сеткой С (рис. 1) разностные аналоги вихря скорости (26) в виде (28) и кинетической энергии записываются следующим образом:
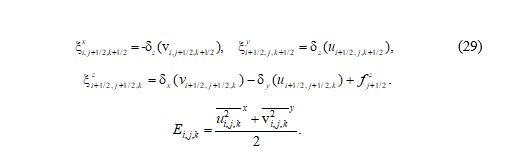
Дискретное уравнение движения (25) при a = x, b = y, g = z и a = y, b = x, g = z приводит к системе уравнений (20), (21), где компоненты абсолютного вихря имеют вид (29).
Перепишем полученные уравнения в следующем виде:
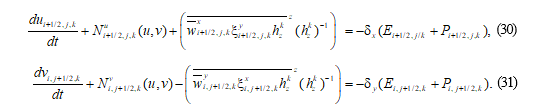
Для описания вертикальной адвекции выбрана схема на минимальном разностном шаблоне, обеспечивающая сохранение энергии в уравнениях движения. Она является частным случаем схемы, представленной в уравнениях (21)–(24). Нетрудно убедиться, что горизонтальные адвективные слагаемые в уравнениях (30), (31) имеют вид
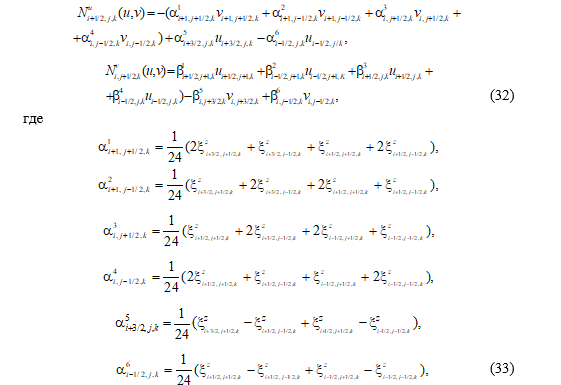
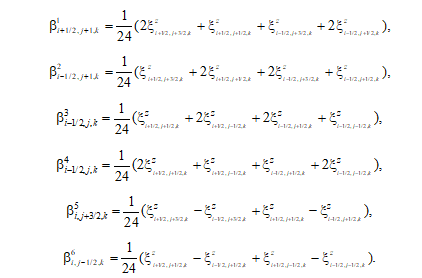
Уравнение для вертикальной компоненты абсолютного вихря скорости в точке 
записывается в виде (a = z в уравнении (27))
Вид последних двух слагаемых в уравнении (34) очевиден.
Аппроксимация (32)–(34) в точности соответствует схеме Аракавы – Лэмба, и поэтому в приближении мелкой воды уравнение (34) обладает двумя квадратичными инвариантами (энергия и потенциальная энстрофия). При выполнении двух квадратичных законов сохранения среднее волновое число не зависит от времени. Поэтому предотвращается систематическая передача энергии к движениям с высокими волновыми числами и тем самым повышается устойчивость численного решения задачи.
Полученная форма записи (25), (27) позволяет выписать аналогичные схемы для двух других компонент вихря скорости.
Заключение
В работе запись схемы Аракавы – Лэмба представлена в виде трех слагаемых, которые отражают разные свойства дискретных уравнений. Первое слагаемое обеспечивает выполнение для дискретной постановки закона сохранения энергии, второе – приводит к схеме, обладающей двумя квадратичными инвариантами для случая бездивергентного течения, прибавление третьего слагаемого соответствует схеме Аракавы – Лэмба. Важной особенностью представленной записи является то, что для второго и третьего слагаемых нет аналогов в системе дифференциальных уравнений. Порядок аппроксимации они не меняют, а на свойства схемы влияют существенным образом. При уменьшении шага сетки они стремятся к нулю, и поэтому их можно интерпретировать как приближение нуля некоторой функцией – 
. Следовательно, подбирая соответствующие разностные аппроксимации нулевой правой части, можно получать разностные схемы с различными свойствами сохранения. Так как таких вариантов бесконечное множество, то необходимо вводить соответствующий формализм поиска схем с заданными характеристиками.
Принципиальный результат заключается в том, что представленная запись позволяет выписать разностные уравнения для горизонтальных компонент вихря скорости, обладающих аналогично схеме Аракавы – Лэмба двумя квадратичными инвариантами.
1. Noether E. Invariante Variationsprobleme // Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen – Mathematisch-Physikalische Klasse. Berlin, 1918. P. 235–257.
2. Arakawa A. Computational design for long-term numerical integration of the equations of fluid motion: Two-dimensional incompressible flow. Part I // Journal of Computational Physics. 1966. Vol. 1, iss. 1. P. 119–143. https://doi.org/10.1016/0021-9991(66)90015-5
3. Arakawa A., Lamb V. R. A potential enstrophy and energy conserving scheme for the shallow water equation // Monthly Weather Review. 1981. Vol. 109, iss. 1. P. 18–36. https://doi.org/10.1175/1520-0493(1981)109<0018:APEAEC>2.0.CO;2
4. Salmon R. A general method for conserving energy and potential enstrophy in shallow-water models // Journal of the Atmospheric Sciences. 2007. Vol. 64, iss. 2. P. 515–531. https://doi.org/10.1175/JAS3837.1
5. Sugibuchi Y., Matsuo T., Sato S. Constructing invariant-preserving numerical schemes based on Poisson and Nambu brackets // JSIAM Letters. 2018. Vol. 10. P. 53–56. https://doi.org/10.14495/jsiaml.10.53
6. Toy M. D., Nair R. D. A potential enstrophy and energy conserving scheme for the shallow-water equations extended to generalized curvilinear coordinates // Monthly Weather Review. 2016. Vol. 145, iss. 3. P. 751–772. https://doi.org/10.1175/MWR-D-16-0250.1
7. Stewart A. L., Dellar P. J. An energy and potential enstrophy conserving numerical scheme for the multi-layer shallow water equations with complete Coriolis force // Journal of Computational Physics. 2016. Vol. 313. P. 99–120. https://doi.org/10.1016/j.jcp.2015.12.042
8. Demyshev S. G. Chislennye eksperimenty po sopostavleniyu dvuh konechno-raznostnyh shem dlya uravneniy dvizheniya v diskretnoy modeli gidrodinamiki Chernogo morya // Morskoy gidrofizicheskiy zhurnal. 2005. № 5. S. 47–59.
9. Demyshev S. G. Nelineynye invarianty diskretnoy sistemy uravneniy dinamiki morya v kvazistaticheskom priblizhenii // Morskoy gidrofizicheskiy zhurnal. 2023. T. 39, № 5. S. 557–583. EDN JWSUUM.
